The center of mass of a system of particles does not depend upon,

(a)

position of particles

(b)

relative distance between particles

(c)

masses of particles

(d)

force acting on particle

A couple produces,

(a)

pure rotation

(b)

pure translation

(c)

rotation and translation

(d)

no motion

A particle is moving with a constant velocity along a line parallel to positive X-axis. The magnitude of its angular momentum with respect to the origin is

(a)

zero

(b)

 increasing with x

(c)

decreasing with x

(d)

remaining constant

A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force 30 N?

(a)

0.25 rad s^-2

(b)

25 rad s^-2

(c)

5 ms^-2 

(d)

25 ms^-2

A closed cylindrical container is partially filled with water. As the container rotates in a horizontal plane about a perpendicular bisector, its moment of inertia

(a)

increases

(b)

decreases

(c)

remains constant

(d)

depends on direction of rotation

A rigid body rotates with an angular momentum L. If its kinetic energy is halved, the angular momentum becomes,

(a)

L

(b)

L/2

(c)

2L

(d)

L/\(\sqrt{2}\)

A particle undergoes uniform circular motion. The angular momentum of the particle remain conserved about,

(a)

the center point of the circle

(b)

the point on the circumference of the circle

(c)

any point inside the circle

(d)

any point outside the circle

A disc of the moment of inertia I_a is rotating in a horizontal plane about its symmetry axis with a constant angular speed \(\omega\). Another disc initially at rest of moment of inertia I_b is dropped coaxially on to the rotating disc. Then, both the discs rotate with the same constant angular speed. The loss of kinetic energy due to friction in this process is,

(a)

\(\frac { 1 }{ 2 } \frac { { I }_{ b }^{ 2 } }{ 2({ I }_{ a }+{ I }_{ b }) } { \omega }^{ 2 }\)

(b)

\(\frac { { I }_{ b }^{ 2 } }{ ({ I }_{ a }+{ I }_{ b }) } { \omega }^{ 2 }\)

(c)

\(\frac { { ({ I }_{ b }-{ I }_{ a }) }^{ 2 } }{ ({ I }_{ a }+{ I }_{ b }) } { \omega }^{ 2 }\)

(d)

\(\frac { 1 }{ 2 } \frac { { { I }_{ b }{ I }_{ b } } }{ ({ I }_{ a }+{ I }_{ b }) } { \omega }^{ 2 }\)

From a disc of radius R a mass M, a circular hole of diameter R, whose rim passes through the center is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis passing through it

(a)

15MR²/32

(b)

13MR²/32

(c)

11MR²/32

(d)

9MR²/32

The ratio of the acceleration for a solid sphere (mass m and radius R) rolling down an incline of angle \(\theta\) without slipping and slipping down the incline without rolling is,

(a)

5: 7

(b)

2: 3

(c)

2: 5

(d)

7: 5

The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is,

(a)

\( \sqrt \frac{4}{3}gh\)

(b)

\( \sqrt \frac{10}{7}gh\)

(c)

\(\sqrt{2gh}\)

(d)

\( \sqrt \frac{1}{2}gh\)

The speed of the center of a wheel rolling on a horizontal surface is v_o.  A point on the rim in level with the center will be moving at a speed of,

(a)

zero

(b)

v_o

(c)

\(\sqrt{2}\)v_o

(d)

2v_o

Two discs of same moment of inertia rotating about their regular axis passing through center and perpendicular to the plane of the disc with angular velocities ω₁ and ω₁. They are brought in to contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is

(a)

\(\frac{1}{4}\)\(I(\omega _{1}-\omega _{2})^2\)

(b)

\(I(\omega _{ 1 }-\omega _{ 2 })^{ 2 }\)

(c)

\(\frac{1}{8}\)\(I(\omega _{1}-\omega _{2})^2\)

(d)

\(\frac{1}{2}I\)\((\omega _{1}-\omega _{2})^2\)

When a mass is rotating in a plane about a fixed point, its angular momentum is directed along

(a)

a line perpendicular to the plane of rotation

(b)

the line making an angle of 45^o to the plane of rotation

(c)

the radius

(d)

tangent to the path

A round object of mass M and radius R rolls down without slipping along an inclined plane. The fractional force, 

(a)

dissipates kinetic energy as heat

(b)

decreases the rotational motion

(c)

decreases the rotational and transnational motion

(d)

converts transnational energy into rotational energy

If force acts on a body, whose line of action does not pass through its CG, then the body will experience ______________

(a)

angular acceleration

(b)

lineal acceleration

(c)

both (a) and (b)

(d)

none

The M.I of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through _____________.

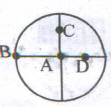(a)

B

(b)

D

(c)

A

(d)

C

M.I. of a ring of mass M and radius R about an axis passing through the centre & perpendicular to the plane is I. What is M.I. about its diameter?

(a)

I

(b)

I/2

(c)

\(I/\sqrt{2}\)

(d)

I + MR²

A solid sphere is rotating in free space. If the radius of the sphere is increased keeping mass same, which one of the following will not be affected?

(a)

M.I

(b)

 Angular momentum

(c)

 Angular velocity

(d)

Rotational K.E.

The reduced mass of two particles having masses m and 2m is _____________.

(a)

2m

(b)

3m

(c)

2m/3

(d)

m/2

When a child sits stationary at one end of a long trolley moving uniformly with some speed on a smooth horizontal plane. The speed of the centre of mass of the system (child and trolley) ________________.

(a)

increases

(b)

decreases

(c)

remains same

(d)

changes

A circular turn table has a block of ice placed at its centre. The system rotates with an angular speed \(ω\) about an axis passing through the centre of the table. If the ice melts on its own without any evaporation, the speed of rotation of the system ________________.

(a)

becomes zero

(b)

remains constant at the same value \(ω\)

(c)

increases to a value greater than \(ω\)

(d)

decreases to a value less than \(ω\)

A solid sphere of radius R is placed on smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of centre of mass, which is correct?

(a)

h=R

(b)

h=2R

(c)

h=0

(d)

no relation between h and R.

The ratio of radius of gyration of a circular ring and a circular disc, of the same mass and radius, about an axis passing through their centres and perpendicular to their planes are _____________.

(a)

1:\(\sqrt{2}\)

(b)

3:2

(c)

2:1

(d)

\(\sqrt{2}\):1

A car of mass 1000 kg negotiates a banked curve of radius 90 m on a frictionless road. If the banking angle is 45°, the speed of the car is _____________.

(a)

20ms^-1

(b)

30ms^-1

(c)

5ms^-1

(d)

10ms^-1

Rotational kinetic energy is given by ___________.

(a)

\(\frac { 1 }{ 2 } \)mv²

(b)

\(\frac { 1 }{ 2 } \)Iv²

(c)

\(\frac { { L }^{ 2 } }{ 2I } \)

(d)

\(\frac { 2I }{ L^{ 2 } } \).

If E is a rotational kinetic energy then angular momentum is ______________.

(a)

\(\sqrt { 2IE } \)

(b)

\(\frac { { E }^{ 2 } }{ 2I } \)

(c)

\(\frac { 2I }{ { E }^{ 2 } } \)

(d)

\(\frac { E }{ { I }^{ 2 }{ \omega }^{ 2 } } \)

The product of torque acting on a body and angular velocity is ______________.

(a)

Energy

(b)

power

(c)

workdone

(d)

kinetic energy

Two rotating bodies A and B of masses m and 2m with moments of inertia I_A and I_B (I_B > I_A) have equal kinetic energy of rotation. If L_A and L_B be their angular momenta respectively, then ______________.

(a)

L_B>L_A

(b)

L_A>L_B

(c)

L_A=\(\frac { { L }_{ B } }{ 2 } \)

(d)

L_A=2L_B

In a two particle system, one particle lies at origin another one lies at a distance of X. Then the position of center of mass of these particles of equal mass is ______________.

(a)

\(\frac{m_2 X_2}{m_1+m_2}\)

(b)

\(\frac{X}{2}\)

(c)

\(\frac{mX}{m_1+m_2}\)

(d)

\(\frac{m_1+m_2}{mX}\)

Moment of inertia of a uniform solid sphere about an axis passing through the center along its diameter is _______________.

(a)

\(\frac { 2 }{ 3 } \)MR²

(b)

\(\frac { 5 }{ 3 } \)MR²

(c)

\(\frac { 7 }{ 5 } \)MR²

(d)

\(\frac { 2 }{ 5 } \)MR²

The ratio of K²/R² of a thin uniform ring about an axis passing through the center and perpendicular to the plane is _____________.

(a)

1

(b)

2

(c)

\(\frac { 1 }{ 2 } \)

(d)

\(\frac { 3 }{ 2 } \)

If the direction of the torque is inward the paper then the rotation is ____________.

(a)

clockwise

(b)

anticlockwise

(c)

straight line

(d)

random direction

If \(\overrightarrow {r}\) and \(\overrightarrow {F}\) are parallel or antiparallel, then the torque is _____________.

(a)

zero

(b)

minimum

(c)

maximum

(d)

infinity

Moment of inertia for bulk object _____________.

(a)

rm²

(b)

rw²

(c)

\(m_ir^{2}_{i}\)

(d)

\(\sum{m_ir^{2}_{i}}\)

The linear momentum and position vector of the planet is perpendicular to each other at

(a)

perihelion and aphelion

(b)

at all points

(c)

only at perihelion

(d)

no point

If the masses of the Earth and Sun suddenly double, the gravitational force between them will

(a)

remain the same

(b)

increase 2 times

(c)

increase 4 times

(d)

decrease 2 times

A planet moving along an elliptical orbit is closest to the Sun at distance r₁ and farthest away at a distance of r₂. If v₁ and v₂ are linear speeds at these points respectively. Then the ratio \({v_1\over v_2}\) is

(a)

\({r_2\over r_1}\)

(b)

\(({r_2\over r_1})^2\)

(c)

\({r_1\over r_2}\)

(d)

\(({r_1\over r_2})^2\)

The time period of a satellite orbiting Earth in a cirular orbit is independent of

(a)

Radius of the orbit

(b)

The mass of the satellite

(c)

Both the mass and radius of the orbit

(d)

Neither the mass nor the radius of its orbit

If the distance between the Earth and Sun were to be doubled from its present value, the number of days in a year would be

(a)

64.5

(b)

1032

(c)

182.5

(d)

730

According to Kepler’s second law, the radial vector to a planet from the Sun sweeps out equal areas in equal intervals of time. This law is a consequence of

(a)

conservation of linear momentum

(b)

conservation of angular momentum

(c)

conservation of energy

(d)

conservation of kinetic energy

The gravitational potential energy of the Moon with respect to Earth is

(a)

always positive

(b)

always negative

(c)

can be positive or negative

(d)

always zero

The kinetic energies of a planet in an elliptical orbit about the Sun, at positions A, B and C are K_A, K_B and K_C respectively. AC is the major axis and SB is perpendicular to AC at the position of the Sun S as shown in the figure. Then
 

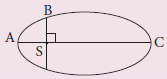(a)

K_A > K_B >K_C

(b)

K_B < K_A < K_C

(c)

K_A < K_B < K_C

(d)

K_B > K_A > K_C

The work done by the Sun’s gravitational force on the Earth is

(a)

always zero

(b)

always positive

(c)

can be positive or negative

(d)

always negative

If the mass and radius of the Earth are both doubled, then the acceleration due to gravity g'

(a)

remains same

(b)

\({g\over 2}\)

(c)

2g

(d)

4g

The magnitude of the Sun’s gravitational field as experienced by Earth is

(a)

same over the year

(b)

decreases in the month of January and increases in the month of July

(c)

decreases in the month of July and increases in the month of January

(d)

increases during day time and decreases during night time

If a person moves from Chennai to Trichy, his weight

(a)

increases

(b)

decreases

(c)

remains same

(d)

increases and then decreases

An object of mass 10 kg is hanging on a spring scale which is attached to the roof of a lift. If the lift is in free fall, the reading in the spring scale is

(a)

98 N

(b)

zero

(c)

49 N

(d)

9.8 N

If the acceleration due to gravity becomes 4 times its original value, then escape speed

(a)

remains same

(b)

2 times of original value

(c)

becomes halved

(d)

4 times of original value

The kinetic energy of the satellite orbiting around the Earth is

(a)

equal to potential energy

(b)

less than potential energy

(c)

greater than kinetic energy

(d)

zero