CBSE 10th Standard Maths Subject Pair of Linear Equation in Two Variables Case Study Questions With Solution 2021
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject Pair of Linear Equation in Two Variables Case Study Questions With Solution 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
From Bengaluru bus stand, if Riddhima buys 2 tickets to Malleswaram and 3 tickets to Yeswanthpur, then total cost is Rs 46; but if she buys 3 tickets to Malleswaram and 5 tickets to Yeswanthpur, then total cost is Rs 74.

Consider the fares from Bengaluru to Malleswaram and that to Yeswanthpur as Rs x and Rs y respectively and answer the following questions.
(i) 1st situation can be represented algebraically as(a) 3x-5y=74 (b) 2x+5y=74 (c) 2x-3y=46 (d) 2x+3y=46 (ii) 2nd situation can be represented algebraically as
(a) 5x + 3y = 74 (b) 5x- 3y= 74 (c) 3x + 5y = 74 (d) 3x-5y=74 (iii), Fare from Ben~aluru to Malleswaram is
(a) Rs 6 (b) Rs 8 (c) Rs 10 (d) Rs 2 (iv) Fare from Bengaluru to Yeswanthpur is
(a) Rs 10 (b) Rs 12 (c) Rs 14 (d) Rs 16 (v) The system oflinear equations represented by both situations has
(a) infinitely many solutions (b) no solution (c) unique solution (d) none of these (a) -
Mr Manoj Jindal arranged a lunch party for some of his friends. The expense of the lunch are partly constant and partly proportional to the number of guests. The expenses amount to Rs 650 for 7 guests and Rs 970 for 11 guests .

Denote the constant expense by Rs x and proportional expense per person by Rs y and answer the following questions.
(i) Represent both the situations algebraically.(a) x + 7y = 650, x + 11y = 970 (b) x - 7y = 650, x - 11y = 970 (c) x+ 11y=650,x+7y=970 (d) 11x + 7y = 650, 11x - 7y = 970 (ii) Proportional expense for each person is
(a) Rs 50 (b) Rs 80 (c) Rs 90 (d) Rs 100 (iii) The fixed (or constant) expense for the party is
(a) Rs 50 (b) Rs 80 (c) Rs 90 (d) Rs 100 (iv) If there would be 15 guests at the lunch party, then what amount Mr Jindal has to pay?
(a) Rs 1500 (b) Rs 1300 (c) Rs 1200 (d) Rs 1290 (v) The system of linear equations representing both the situations will have
(a) unique solution (b) no solution (c) infinitely many solutions (d) none of these (a) -
A boat in the river Ganga near Rishikesh covers 24 km upstream and 36 km downstream in 6 hours while it covers 36 km upstream and 24 km downstream in \(6 \frac{1}{2}\) hours. Consider speed of the boat in still water be x km/hr and speed of the stream be y km/hr and answer the following questions.

(i) Represent the 1st situation algebraically.\((a) \frac{24}{x-y}+\frac{36}{x+y}=6\) \((b) \frac{24}{x+y}+\frac{36}{x-y}=6\) \((c) 24 x+36 y=6\) \((d) 24 x-36 y=6\) (ii) Represent the 2nd situation algebraically.
\((a) \frac{36}{x+y}+\frac{24}{x-y}=\frac{13}{2}\) \((b) \frac{36}{x-y}+\frac{24}{x+y}=\frac{13}{2}\) \((c) 36 x-24 y=\frac{13}{2}\) \((d) 36 x+24 y=\frac{13}{2}\) (iii) If u \(=\frac{1}{x-y} \text { and } v=\frac{1}{x+y}, \text { then } u=\)
\((a) \frac{1}{4}\) \((b) \frac{1}{12}\) \((c) \frac{1}{8}\) \((d) \frac{1}{6}\) (iv) Speed of boat in still water is
(a) 4 km/hr (b) 6 km/hr (c) 8 km/hr (d) 10 krn/hr (v) Speed of stream is
(a) 3 km/hr (b) 4 km/hr (c) 2 km/hr (d) 5 km/hr (a) -
Puneet went for shopping in the evening by metro with his father who is an expert in mathematics. He told Puneet that path of metro A is given by the equation 2x + 4y = 8 and path of metro B is given by the equation 3x + 6y = 18. His father put some questions to Puneet. Help Puneet to solve the questions.
(i) Equation 2x + 4y = 8 intersects the x-axis and y-axis respectively at(a) (4,0), (0, 2) (b) (0,4), (2,0) (c) (4,0), (2,0) (d) (0,4), (0, 2) (ii) Equation 3x + 6y = 18 intersects the x-axis and y-axis respectively at
(a) (6,0), (0, 8) (b) (0,6), (0, 8) (c) (6,0), (0, 3) (d) (0,6), (0, 3) (iii) Coordinates of point of intersection of two given equations are
(a) (1,2) (b) (2,4) (c) (3,7) (d) does not exist (iv) Represent the equations, 2x + 4y = 8 and 3x + 6y = 18 graphically.
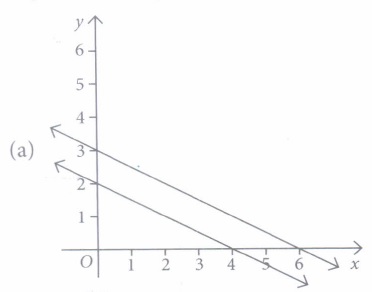
(d) None of these (v) System oflinear equations represented by two given lines is
(a) inconsistent (b) having infinitely many solutions (c) consistent (d) overlapping each other (a) -
Raman usually go to a dry fruit shop with his mother. He observes the following two situations.
On 1st day: The cost of 2 kg of almonds and 1 kg of cashew was Rs 1600.
On 2nd day: The cost of 4 kg of almonds and 2 kg of cashew was Rs 3000.
Denoting the cost of 1 kg almonds by Rs x and cost of 1 kg cashew by Rs y, answer the following questions.

(i) Represent algebraically the situation of day-I.(a) x + 2y = 1000 (b) 2x + y = 1600 (c) x - 2y = 1000 (d) 2x - y = 1000 (ii) Represent algebraically the situation of day- II.
(a) 2x + y= 1500 (b) 2x- y= 1500 (c) x + 2y=1500 (d) 2x + y = 750 (iii) The linear equation represented by day-I, intersect the x axis at
(a) (0,800) (b) (0,-800) (c) (800,0) (d) (-800,0) (iv) The linear equation represented by day-II, intersect the y-axis at
(a) (1500,0) (b) (0, -1500) (c) (-1500,0) (d) (0,1500) (v) Linear equations represented by day-I and day -II situations, are
(a) non parallel (b) parallel (c) intersect at one point (d) overlapping each other. (a)
Case Study Questions
*****************************************
CBSE 10th Standard Maths Subject Pair of Linear Equation in Two Variables Case Study Questions With Solution 2021 Answer Keys
-
(i) (d): 1st situation can be represented algebraically as 2x + 3y = 46
(ii) (c): 2nd situation can be represented algebraically as 3x + 5y = 74
(iii) (b): We have, 2x + 3y = 46 .........(i)
3x+5y=74........... (ii)
Multiplying (i) by 5 and (ii) by 3 and then subtracting,
we get 10x - 9x = 230 - 222 \(\Rightarrow\) x = 8
\(\therefore\) Fare from Bengaluru to Malleswaram is Rs 8.
(iv) (a): Putting the value of x in equation (i), we get
3y = 46 - 2 x 8 = 30 \(\Rightarrow\) Y = 10
\(\therefore\) Fare from Bengaluru to Yeswanthpur is Rs 10.
(v) (c): We have, a1 = 2, b1, = 3, c1 = -46 and
\(a_{2}=3, b_{2}=5, c_{2}=-74 \)
\(\therefore \quad \frac{a_{1}}{a_{2}}=\frac{2}{3}, \frac{b_{1}}{b_{2}}=\frac{3}{5}, \frac{c_{1}}{c_{2}}=\frac{-46}{-74}=\frac{23}{37} \Rightarrow \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Thus system oflinear equations has unique solution. -
(i) (a): 1st situation can be represented as x + 7y = 650 ...(i) and
2nd situation can be represented as x + 11y = 970 ...(ii)
(ii) (b): Subtracting equations (i) from (ii), we get
\(4 y=320 \Rightarrow y=80\)
\(\therefore\) Proportional expense for each person is Rs 80.
(iii) (c): Puttingy = 80 in equation (i), we get
x + 7 x 80 = 650 \(\Rightarrow\) x = 650 - 560 = 90
\(\therefore\) Fixed expense for the party is Rs 90
(iv) (d): If there will be 15 guests, then amount that Mr Jindal has to pay = Rs (90 + 15 x 80) = Rs 1290
(v) (a): We have a1 = 1, b1 = 7, c1 = -650 and
\(a_{2}=1, b_{2}=11, c_{2}=-970 \)
\(\therefore \frac{a_{1}}{a_{2}}=1, \frac{b_{1}}{b_{2}}=\frac{7}{11}, \frac{c_{1}}{c_{2}}=\frac{-650}{-970}=\frac{65}{97}\)
\(\text { Here, } \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
Thus, system of linear equations has unique solution. -
Speed of boat in upstream = (x - y)km/hr and speed of boat in downstream = (x + y)km/hr.
(i) (a): 1st situation can be represented algebraically as \(\frac{24}{x-y}+\frac{36}{x+y}=6\)
(ii) (b): 2nd situation can be represented algebraically as \(\frac{36}{x-y}+\frac{24}{x+y}=\frac{13}{2}\)
(iii) (c) : Putting \(\frac{1}{x-y}=u \text { and } \frac{1}{x+y}=v\)
we get,
24u + 36v = 6 and 36u + 24v = 13/2
Solving the above equations, we get u \(=\frac{1}{8}, v=\frac{1}{12}\)
(iv) (d): \(\because u=\frac{1}{8}=\frac{1}{x-y} \Rightarrow x-y=8\) ........(i)
\(\text { and } v=\frac{1}{12}=\frac{1}{x+y} \Rightarrow x+y=12\) .........(ii)
Adding equations (i) from (ii), we get 2x = 20 \(\Rightarrow\) x = 10
\(\therefore\) Speed of boat in still water = 10 km/hr -.
(v) (c): From equation (i), 10 - y = 8 \(\Rightarrow\) y = 2
\(\therefore\) Speed of stream = 2 km/hr. -
(i) (a): At x-axis, y = 0
\(\therefore\) 2x + 4y = 8 \(\Rightarrow\) x = 4
At y-axis, x = 0
\(\therefore\) 2x + 4y = 8 \(\Rightarrow\) Y = 2
\(\therefore\) Required coordinates are (4, 0), (0, 2).
(ii) (c): At x-axis, y = 0
\(\therefore\) 3x + 6y = 18 \(\Rightarrow\) 3x = 18 \(\Rightarrow\) x = 6
At y-axis, x = 0
\(\therefore\) 3x + 6y = 18 \(\Rightarrow\) 6y = 18 \(\Rightarrow\) Y = 3
\(\therefore\) Required coordinates are (6, 0), (0, 3).
(iii) (d): Since, lines are parallel. So, point of intersection of these lines does not exist.
(iv) (a)
(v) (a): Since the lines are parallel.
\(\therefore\) These equations have no solution i.e., the given system of linear equations is inconsistent. -
(i) (b): Algebraic representation of situation of day-I is 2x + y = 1600.
(ii) (a): Algebraic representation of situation of day- II is 4x + 2y = 3000 \(\Rightarrow\) 2x + y = 1500.
(iii) (c) : At x-axis, y = 0
\(\therefore\) At y = 0, 2x + y = 1600 becomes 2x = 1600
\(\Rightarrow\) x = 800
\(\therefore\) Linear equation represented by day- I intersect the x-axis at (800, 0).
(iv) (d) : At y-axis, x = 0
\(\therefore\) 2x + Y = 1500 \(\Rightarrow\) y = 1500
\(\therefore\) Linear equation represented by day-II intersect the y-axis at (0, 1500).
(v) (b): We have, 2x + y = 1600 and 2x + y = 1500
Since \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}} \text { i.e., } \frac{1}{1}=\frac{1}{1} \neq \frac{16}{15}\)
\(\therefore\) System of equations have no solution.
\(\therefore\) Lines are parallel.
Case Study Questions

























