CBSE 12th Standard Maths Subject Case Study Questions 2021
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 12 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Maths Subject Case Study Questions 2021
12th Standard CBSE
-
Reg.No. :
Maths
-
Deepa rides her car at 25 km/hr, She has to spend Rs. 2 per km on diesel and if she rides it at a faster speed of 40 km/hr, the diesel cost increases to Rs. 5 per km. She has Rs. 100 to spend on diesel. Let she travels x kms with speed 25 km/hr and y kms with speed 40 km/hr. The feasible region for the LPP is shown below:
Based on the above information, answer the following questions
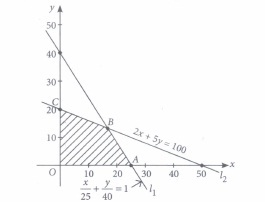
Based on the above information, answer the following questions.
(i) What is the point of intersection of line l1 and l2,\(\text { (a) }\left(\frac{40}{3}, \frac{50}{3}\right)\) \(\text { (b) }\left(\frac{50}{3}, \frac{40}{3}\right)\) \(\text { (c) }\left(\frac{-50}{3}, \frac{40}{3}\right)\) \(\text { (d) }\left(\frac{-50}{3}, \frac{-40}{3}\right)\) (ii) The corner points of the feasible region shown in above graph are
\(\text { (a) }(0,25),(20,0),\left(\frac{40}{3}, \frac{50}{3}\right)\) \(\text { (b) }(0,0),(25,0),(0,20)\) \(\text { (c) }(0,0),\left(\frac{40}{3}, \frac{50}{3}\right),(0,20)\) \(\text { (d) }(0,0),(25,0),\left(\frac{50}{3}, \frac{40}{3}\right),(0,20)\) (iii) If Z = x + y be the objective function and max Z = 30. The maximum value occurs at point
\(\text { (a) }\left(\frac{50}{3}, \frac{40}{3}\right)\) (b) (0, 0) (c) (25, 0) (d) (0, 20) (iv) If Z = 6x - 9y be the objective function, then maximum value of Z is
(a) -20 (b) 150 (c) 180 (d) 20 (v) If Z = 6x + 3y be the objective function, then what is the minimum value of Z?
(a) 120 (b) 130 (c) 0 (d) 150 (a) -
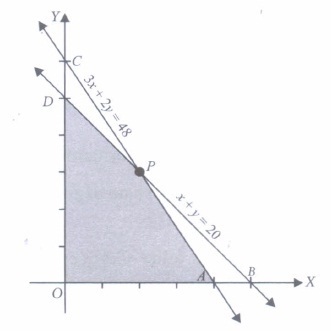
Suppose a dealer in rural area wishes to purpose a number of sewing machines. He has only Rs. 5760 to invest and has space for at most 20 items for storage. An electronic sewing machine costs him Rs. 360 and a manually operated sewing machine Rs. 240. He can sell an electronic sewing machine at a profit of Rs. 22 and a manually operated sewing machine at a profit of Rs. 18.
Based on the above information, answer the following questions.
(i) Let x and y denotes the number of electronic sewing machines and manually operated sewing machines purchased by the dealer. If it is assume that the dealer purchased atleast one of the given machines, then(a) x + y ≥ 0 (b) x + y < 0 (c) x + y > 0 (d) x + y ≤ 0 (ii) Let the constraints in the given problem is represented by the following inequalities
x + y ≤ 20
360x + 240y ≤ 5760
x, y ≥ 0
Then which of the following point lie in its feasible region.(a) (0, 24) (b) (8, 12) (c) (20, 2) (d) None of these (iii) If the objective function of the given problem is maximise z = 22x + 18y, then its optimal value occur at
(a) (0, 0) (b) (16, 0) (c) (8, 12) (d) (0, 20) (iv) Suppose the following shaded region APDO, represent the feasible region corresponding to mathematical formulation. of given problem. Then which of the following represent the coordinates of one of its corner points.
(a) (0, 24) (b) (12, 8) (c) (8, 12) (d) (6, 14) (v) If an LPP admits optimal solution at two consecutive vertices of a feasible region, then
(a) the required optimal solution is at the midpoint of the line joining two points. (b) the optimal solution occurs at every point on the line joining these two points. (c) the LPP under consideration is not solvable. (d) the LPP under consideration must be reconstructed. (a) -
A student Arun is running on a playground along the curve given by y = x2 + 7. Another student Manita standing at point (3, 7) on playground wants to hit Arun by paper ball when Arun is nearest to Manita .
Based on above information, answer the following questions.
(i) Arun's position at any value of x will be(a) x2,y-7 (b) (x2,y+7) (c) (x, x2 + 7) (d) (x2,x-7) (ii) Distance (say D) between Arun and Manita will be
(a) (x - 1)(2x2 + 2x + 3) (b) (x-3)2+x4 (c) \(\sqrt{(x-3)^{2}+x^{4}}\) (d) \(\sqrt{(x-1)\left(2 x^{2}+2 x+3\right)}\) (iii) For which real value(s) of x, first derivative of D2 w.r.t. 'x' will Vanish?
(a) 1 (b) 2 (c) 3 (d) 4 (iv) Find the position of Arun when Manita will hit the paper hall.
(a) (5, 32) (b) (1, 8) (c) (3, 7) (d) (3, 16) (v) The minimum value of D is
(a) 3 (b) \(\sqrt{3}\) (c) 5 (d) \(\sqrt{5}\) (a) -
Rohan, a student of class XII, visited his uncle's flat with his father. He observe that the window of the house is in the form of a rectangle surmounted by a semicircular opening having perimeter 10m as shown in the figure.
(i) If x and y represents the length and breadth of the rectangular region, then relation between x and y can be represented as(a) \(x+y+\frac{\pi}{2}=10\) \(x+2 y+\frac{\pi x}{2}=10\) (c) 2x + 2y = 10 (d) \(x+2 y+\frac{\pi}{2}=10\) (ii) The area (A) of the window can be given by
(a) \(A=x-\frac{x^{3}}{8}-\frac{x^{2}}{2}\) (b) \(A=5 x-\frac{x^{2}}{2}-\frac{\pi x^{2}}{8}\) (c) \(A=x+\frac{\pi x^{3}}{8}-\frac{3 x^{2}}{8}\) (d) \(A=5 x+\frac{x^{2}}{2}+\frac{\pi x^{2}}{8}\) (iii) Rohan is interested in maximizing the area of the whole window, for this to happen, the value of x should be
(a) \(\frac{10}{2-\pi}\) (b) \(\frac{20}{4-\pi}\) (c) \(\frac{20}{4+\pi}\) (d) \(\frac{10}{2+\pi}\) (iv) Maximum area of the window is
(a) \(\frac{30}{4-\pi}\) (b) \(\frac{30}{4+\pi}\) (c) \(\frac{50}{4-\pi}\) (d) \(\frac{50}{4+\pi}\) (v) For maximum value of A, the breadth of rectangular part of the window is
(a) \(\frac{10}{4+\pi}\) (b) \(\frac{10}{4-\pi}\) (c) \(\frac{20}{4+\pi}\) (d) \(\frac{20}{4-\pi}\) (a) -
A student is preparing for the competitive examinations LIC AAO, SSC CGL and Bank P.O. The probabilities that the student is selected independently in competitive examination of LIC AAO, SSC CGL and Bank P.O. are a, b and c respectively. Of these examinations, students has 50% chance of selection in at least one, 40% chance of selection in at least two and 30% chance of selection in exactly two examinations.

Based on the above information, answer the following questions.
(i) The value of a + b + c - ab - bc - ca + abc is(a) 0.3 (b) 0.5 (c) 0.7 (d) 0.6 (ii) The value of ab + bc + ac - 2abc is
(a) 0.5 (b) 0.3 (c) 0.4 (d) 0.6 (iii) The value of abc is
(a) 0.1 (b) 0.5 (c) 0.7 (d) 0.3 (iv) The value of ab + bc + dc is
(a) 0.1 (b) 0.6 (c) 0.5 (d) 0.3 (v) The value of a + b + c is
(a) 1 (b) 1.5 (c) 1.6 (d) 1.4 (a) -
Teams A, B, C went for playing a tug of war game. Teams A, B, C have attached a rope to a metal ring and is trying to pull the ring into their own area (team areas shown below).
Team A pulls with force F1 = \(\hat{4}+\hat{0} \hat{j}\) KN
Team B ⟶ F2 = \(-2 \hat{i}+4 \hat{j}\) KN
Team C ⟶ F3 = \(-3 \hat{i}-3 \hat{j}\) KN
Based on the above information, answer the following questions.
(i) Which team will win the game ?(a) Team B (b) Team A (c) Team C (d) No one (ii) What is the magnitude of the teams combined force ?
(a) 7 KN (b) 1.4 KN (c) 1.5 KN (d) 2 KN (iii) In what direction is the ring getting pulled?
(a) 2.0 radian (b) 2.5 radian (c) 2.4 radian (d) 3 radian (iv) What is the magnitude of the force of Team B?
(a) 2\(\sqrt 5\) KN (b) 6 KN (c) 2 KN (d) \(\sqrt 6\) KN (v) How many KN force is applied by Team A?
(a) 5 KN (b) 4 KN (c) 2 KN (d) 16 KN (a) -
Varun and Isha decided to play with dice to keep themselves busy at home as their schools are closed due to coronavirus pandemic. Varun throw a dice repeatedly until a six is obtained. He denote the number of throws required by X.

Based on the above information, answer the following questions.
(i) The probability that X = 2 equals(a) \(\frac{1}{6}\) (b) \(\frac{5}{6^2}\) (c) \(\frac{5}{3^6}\) (d) \(\frac{1}{6^3}\) (ii) The probability that X = 4 equals
(a) \(\frac{1}{6^4}\) (b) \(\frac{1}{6^6}\) (c) \(\frac{5^3}{6^4}\) (d) \(\frac{5}{6^4}\) (iii) The probability that X ≥ 2 equals
(a) \(\frac{25}{216}\) (b) \(\frac{1}{36}\) (c) \(\frac{5}{6}\) (d) \(\frac{25}{36}\) (iv) The value of P(X ≥ 6) is
(a) \(\frac{5^5}{6^4}\) (b) \(1-\frac{5^3}{6^5}\) (c) \(\frac{5^3 \times 61}{6^5}\) (d) \(\frac{5^3}{6^4}\) (v) The probability that X > 3 equals
(a) \(\frac{36}{25}\) (b) \(\frac{5^3}{6^5}\) (c) \(\frac{5}{6}\) (d) \(\frac{5^3}{6^3}\) (a) -
Ishaan left from his village on weekend. First, he travelled up to temple. After this, he left for the zoo. After this he left for shopping in a mall. The positions of Ishaan at different places is given in the following graph.
Based on the above information, answer the following questions.
(i) Position vector of B is(a) \(3 \hat{i}+5 \hat{j}\) (b) \(5 \hat{i}+3 \hat{j}\) (c) \(-5 \hat{i}-3 \hat{j}\) (d) \(-5 \hat{i}+3 \hat{j}\) (ii) Position vector of D is
(a) \(5 \hat{i}+3 \hat{j}\) (b) \(3 \hat{i}+5 \hat{j}\) (c) \(8 \hat{i}+9 \hat{j}\) (d) \(9 \hat{i}+8 \hat{j}\) (iii) Find the vector \(\overrightarrow{B C}\) in terms of \(\hat{i}, \hat{j}\).
(a) \( \hat{i}-2 \hat{j}\) (b) \( \hat{i}+2 \hat{j}\) (c) \(2\hat{i}+ \hat{j}\) (d) \(2\hat{i}- \hat{j}\) (iv) Length of vector \(\overrightarrow{A D}\) is
(a) \(\sqrt 67\) units (b) \(\sqrt 85\) units (c) 90 units (d) 100 units (v) If \(\vec{M}=4 \hat{\jmath}+3 \hat{k}\) , then its unit vector
(a) \(\frac{4}{5} \hat{j}+\frac{3}{5} \hat{k}\) (b) \(\frac{4}{5} \hat{j}-\frac{3}{5} \hat{k}\) (c) \(-\frac{4}{5} \hat{j}+\frac{3}{5}\hat{k}\) (d) \(-\frac{4}{5} \hat{j}-\frac{3}{5} \hat{k}\) (a) -
Consider the following equation of curve I' = 4x and straight line x + y = 3.
Based on the above information, answer the following questions.
(i) The line x + y = 3 cuts the x-axis and y-axis respectively at(a) (0, 2), (2, 0) (b) (3, 3), (0, 0) (c) (0, 3), (3, 0) (d) (3, 0), (0, 3) (ii) Point(s) of intersection of two given curves is (are)
(a) (1, -2), (-9, 6) (b) (2, 1), (-6, 9) (c) (1, 2), (9, -6) (d) None of these (iii) Which of the following shaded portion represent the area bounded by given curves?
(iv) Value of the integral \(\int_{-6}^{2}(3-y) d y\) is(a) 10 (b) 20 (c) 30 (d) 40 (v) Value of area bounded by given curves is
(a) 56 sq. units (b) \(\frac{63}{5} \text { sq; units }\) (c) \(\frac{64}{3} \text { sq. units }\) (d) 31 sq. units (a) -
Location of three houses of a society is represented by the points A(-1, 0), B(1, 3) and C(3, 2) as shown in figure. Based on the above information, answer the following questions
(i) Equation of line AB is(a) \(y=\frac{3}{2}(x+1)\) (b) \(y=\frac{3}{2}(x-1)\) (c) \(y=\frac{1}{2}(x+1)\) (d) \(y=\frac{1}{2}(x-1)\) (ii) Equation of line BC is
(a) \(y=\frac{1}{2} x-\frac{7}{2}\) (b) \(y=\frac{3}{2} x-\frac{7}{2}\) (c) \(y=\frac{-1}{2} x+\frac{7}{2}\) (d) \(y=\frac{3}{2} x+\frac{7}{2}\) (iii) Area of region ABCD is
(a) 2 sq. units (b) 4 sq. units (c) 6 sq. units (d) 8 sq. units (iv) Area of \(\Delta A D C\) is
(a) 4 sq. units (b) 8 sq. units (c) 16 sq. units (d) 32 sq. units (iv) Area of \(\Delta A B C\) is
(a) 3 sq. units (b) 4 sq. units (c) 5 sq. units (d) 6 sq. units (a) -
Three slogans on chart papers are to be placed on a school bulletin board at the points A, Band C displaying A (Hub of Learning), B (Creating a better world for tomorrow) and C (Education comes first). The coordinates of these points are (1, 4, 2), (3, -3, -2) and (-2, 2, 6) respectively.
Based on the above information, answer the following questions.
(i) Let \(\vec{a}\), \(\vec{b}\)and \(\vec{c}\) be the position vectors of points A, B and C respectively, then \(\vec{a}\) + \(\vec{b}\)+ \(\vec{c}\) is equal to(a) \(2 \hat{i}+3 \hat{j}+6 \hat{k} \) (b) \(2 \hat{i}-3 \hat{j}-6 \hat{k}\) (c) \(2 \hat{i}+8 \hat{j}+3 \hat{k} \) (d) \(2(7 \hat{i}+8 \hat{j}+3 \hat{k})\) (ii) Which of the following is not true?
(a) \(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}=\overrightarrow{0}\) (b) \(\overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{A C}=\overrightarrow{0}\) (c) \(\overrightarrow{A B}+\overrightarrow{ BC}-\overrightarrow{C A}=\overrightarrow{0}\) (d) \(\overrightarrow{A B}-\overrightarrow{C B}+\overrightarrow{C A}=\overrightarrow{0}\) (iii) Area of \(\Delta\)ABC is
(a) 19 sq. units (b) \(\sqrt 1937 sq. unit\) (c) \(\frac{1}{2}\sqrt 1937 sq. unit\) (d) \(\sqrt 1837 sq. unit\) (iv) Suppose, if the given slogans are to be placed on a straight line, then the value of \(|\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}|\) will be equal to
(a) -1 (b) -2 (c) 2 (d) 0 (v) If \(\vec{a}=2 \hat{i}+3 \hat{j}+6 \hat{k}\) then unit vector in the direction of vector \(\vec{a}\)is
(a) \(\frac{2}{7} \hat{i}-\frac{3}{7} \hat{j}-\frac{6}{7} \hat{k}\) (b) \(\frac{2}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{6}{7} \hat{k}\) (c) \(\frac{3}{7} \hat{i}+\frac{2}{7} \hat{j}+\frac{6}{7} \hat{k}\) (d) None of these (a) -
A football match is organised between students of class XII of two schools, say school A and school B. For which a team from each school is chosen. Remaining students of class XII of school A and B are respectively sitting on the plane represented by the equation \(\vec{r} \cdot(\hat{i}+\hat{j}+2 \hat{k})=5 \text { and } \vec{r} \cdot(\hat{i}-\hat{j}+\hat{k})=6\) ,to cheer up the team of their respective schools.

Based on the above information, answer the following questions.
(i) The cartesian equation of the plane on which students of school A are seated is(a) 2x - y +z = 8 (b) 2x + y + z = 8 (c) x + y + 2z = 5 (d) x + y + z = 5 (ii) The magnitude of the normal to the plane on which students of school B are seated, is
(a) \(\sqrt 5\) (b) \(\sqrt 6\) (c) \(\sqrt 3 \) (d) \(\sqrt 2\) (iii) The intercept form of the equation of the plane on which students of school B are seated, is
(a) \(\frac{x}{6}+\frac{y}{6}+\frac{z}{6}=1\) (b) \(\frac{x}{3}+\frac{y}{(-6)}+\frac{z}{6}=1\) (c) \(\frac{x}{3}+\frac{y}{6}+\frac{z}{6}=1\) (d) \(\frac{x}{3}+\frac{y}{6}+\frac{z}{3}=1\) (iv) Which of the following is a student of school B?
(a) Mohit sitting at (1, 2, 1) (b) Ravi sitting at (0,1,2) (c) Khushi sitting at (3, 1, 1) (d) Shewta sitting at (2, -1, 2) (v) The distance of the plane, on which students of school B are seated, from the origin is
(a) 6 units (b) \(\frac{1}{\sqrt{6}}\) units (c) \(\frac{5}{\sqrt{6}}\) units (d) \(\sqrt 6\) units (a) -
Consider the following equations of curves y = cos x, y = x + 1 and y = 0. On the basis of above information, answer the following questions.
(i) The curves y = cos x and y = x + 1 meet at(a) (1, 0) (b) (0, 1) (c) (1, 1) (d) (0,0) (ii) y = cos x meet the x-axis at
(a) \(\left(\frac{-\pi}{2}, 0\right)\) (b) \(\left(\frac{\pi}{2}, 0\right)\) (c) both (a) and (b) (d) None of these (iii) Value of the integral \(\int_{-1}^{0}(x+1) d x\) is
(a) \(\frac{1}{2}\) (b) \(\frac{2}{3}\) (c) \(\frac{3}{4}\) (d) \(\frac{1}{3}\) (iv) Value of the integral \(\int_{0}^{\pi / 2} \cos x d x\) is
(a) 0 (b) -1 (c) 2 (d) 1 (v) Area bounded by the given curves is
(a) \(\frac{1}{2} \mathrm{sq} . \text { unit }\) (b) \(\frac{3}{2} \text { sq. units }\) (c) \(\frac{3}{4} \text { sq. unit }\) (d) \(\frac{1}{4} \text { sq. unit }\) (a) -
Suppose the floor of a hotel is made up of mirror polished Kota stone. Also, there is a large crystal chandelier attached at the ceiling of the hotel. Consider the floor of the hotel as a plane having equation x - 2y + 2z = 3 and crystal chandelier at the point (3, -2, 1).

Based on the above information, answer the following questions.
(i) The d.r's of the perpendicular from the point (3, -2, 1) to the plane x - 2y + 2z = 3, is(a) < 1,2,2 > (b) < 1, - 2, 2 > (c) < 2,1,2 > (d) < 2, -1, 2 > (ii) The length of the perpendicular from the point (3, -2, 1) to the plane x - 2y + 2z = 3, is
(a) \(\frac{2}{3}\)units (b) 3 units (c) 2 units (d) none of these (iii) The equation of the perpendicular from the point (3, -2, 1) to the plane x - 2y + 2z = 3, is
(a) \(\frac{x-3}{1}=\frac{y-2}{-2}=\frac{z-1}{2}\) (b) \(\frac{x-3}{1}=\frac{y+2}{-2}=\frac{z-1}{2}\) (c) \(\frac{x+3}{1}=\frac{y+2}{-2}=\frac{z-1}{2}\) (d) none of these (iv) The equation of plane parallel to the plane x - 2y + 2z = 3, which is at a unit distance from the point (3, -2, 1) is
(a) x - 2y + 2z = 0 (b) x - 2y + 2z = 6 (c) x - 2y + 2z = 12 (d) Both (b) and (c) (v) The image of the point (3, -2, 1) in the given plane is
(a) \(\left(\frac{5}{3}, \frac{2}{3}, \frac{-5}{3}\right)\) (b) \(\left(\frac{-5}{3}, \frac{-2}{3}, \frac{5}{3}\right)\) (c) \(\left(\frac{-5}{3}, \frac{2}{3}, \frac{5}{3}\right)\) (d) none of these (a) -
A thermometer reading 800P is taken outside. Five minutes later the thermometer reads 60°F. After another 5 minutes the thermometer reads 50of At any time t the thermometer reading be TOP and the outside temperature be SoF.
Based on the above information, answer the following questions.
(i) If \(\lambda\) is positive constant of proportionality, then \(\frac{d T}{d t}\) is(a) \(\lambda(T-S)\) (b) \(\lambda(T+S)\) (c) \(\lambda T S\) (d) \(-\lambda(T-S)\) (ii) The value of T(S) is
(a) 300F (b) 40oF (c) 50oF (d) 60oF (iii) The value of T(10) is
(a) 50oF (b) 40oF (c) 50oF (d) 60oF (iv) Find the general solution of differential equation formed in given situation.
(a) logT=St+c (b) \(\log (T-S)=-\lambda t+c\) (c) log S = tT + c (d) \(\log (T+S)=\lambda t+c\) (v) Find the valiie of constant of integration c in the solution of differential equation formed in given situation.
(a) log (60 -S) (b) log (80 + S) (c) log (80 - S) (d) log (60 + S) (a)
Case Study Questions
*****************************************
CBSE 12th Standard Maths Subject Case Study Questions 2021 Answer Keys
-
(i) (b): Let B(x, y) be the point of intersection of the given lines
2x + 5y = 100 ....(i)
and \(\frac{x}{25}+\frac{y}{40}=1 \Rightarrow 8 x+5 y=20\)...(ii)
Solving (i) and (ii), we get
\(x=\frac{50}{3}, y=\frac{40}{3}\)
ஃ The point of intersection \(B(x, y)=\left(\frac{50}{3}, \frac{40}{3}\right)\)
(ii) (d): The corner points of the feasible region shown in the given graph are
\((0,0), A(25,0), B\left(\frac{50}{3}, \frac{40}{3}\right), C(0,20)\)
(iii) (a): Here Z = x + yCorner Points Value of Z = x + y (0,0) 0 (25,0) 25 \(\left(\frac{50}{3}, \frac{40}{3}\right)\) 30 ⇠ Maximum (0,20) 20 Thus, max Z = 30 occurs at point \(\left(\frac{50}{3}, \frac{40}{3}\right)\)
(iv) (b):Corner Points Value of Z = 6x - 9y (0,0) 0 (25,0) 150 ⇠ Maximum \(\left(\frac{50}{3}, \frac{40}{3}\right)\) -20 (0,20) -180 (v) (c):
Corner Points Value of Z = 6x + 3y (0,0) 0 ⇠ Maximum (25,0) 150 \(\left(\frac{50}{3}, \frac{40}{3}\right)\) 140 (0,20) 60 -
(i) (c)
(ii) (b): Since (8, 12) satisfy all the inequalities therefore (8, .1.2) is the point in its feasible region.
(iii) (c) : At (0, 0), z = 0
At (16, 0), z = 352
At (8, 12), z = 392
At (0, 20), z = 360
It can be observed that max z occur at (8, 12). Thus, z will attain its optimal value at (8, 12).
(iv) (c) : We have, x + y = 20 ... (i)
and 3x + 2y = 48.. (ii)
On solving (i) and (ii), we get
X = 8, y = 12.
Thus, the coordinates of P are (8,12) and hence (8, 12) is one of its corner points.
(v) (b): The optimal solution occurs at every point on the line joining these two points. -
(i) (c) : For all values of x, y = x2 + 7
\(\therefore\) Arun's position at any point of x will be (x, x2+ 7)
(ii) (c) : Distance between
Arun and Manita, i.e., D
\(=\sqrt{(x-3)^{2}+\left(x^{2}+7-7\right)^{2}}\)
\(=\sqrt{(x-3)^{2}+x^{4}}\)
(iii) (a) : We have \(D=\sqrt{(x-3)^{2}+x^{4}}\)
\(\therefore \quad D^{2}=(x-3)^{2}+x^{4}\)
Now, \(\frac{d}{d x}\left(D^{2}\right)=2(x-3)+4 x^{3}=0\)
\(\Rightarrow 4 x^{3}+2 x-6=0 \Rightarrow 2 x^{3}+x-3=0\)
\(\Rightarrow \quad(x-1)\left(2 x^{2}+2 x+3\right)=0\)
\(\therefore\) x = 1
(\(\therefore\) 2x2 + 2x + 3 = 0 will give imaginary values)
(iv) (d) : We have,\(D=\sqrt{(x-3)^{2}+x^{4}}\)
\(D^{\prime}(x)=\frac{2(x-3)+4 x^{3}}{2 \sqrt{(x-3)^{2}+x^{4}}}=0\)
\(\Rightarrow 2 x^{3}+x-3=0\)
\(\Rightarrow x=1\)
Clearly, D"(x) at x = 1 is > 0
\(\therefore\) Value of x for which Dwill be minimum is 1
For x = 1, y = 8.
Thus, the required position is (1, 8).
(v) (d) : Minimum value of \(D=\sqrt{(1-3)^{2}+(1)^{4}}\)
\(=\sqrt{4+1}=\sqrt{5}\) -
(i) (b) : Given, perimeter of window = 10 m
\(\therefore\) x + y + y + perimeter of semicircle = 10
\(\Rightarrow x+2 y+\pi \frac{x}{2}=10\)
(ii) (b) : \(A=x \cdot y+\frac{1}{2} \pi\left(\frac{x}{2}\right)^{2}\)
\(=x\left(5-\frac{x}{2}-\frac{\pi x}{4}\right)+\frac{1}{2} \frac{\pi x^{2}}{4}\left[\because \text { From }(\mathrm{i}), y=5-\frac{x}{2}-\frac{\pi x}{4}\right]\)
\(=5 x-\frac{x^{2}}{2}-\frac{\pi x^{2}}{4}+\frac{\pi x^{2}}{8}=5 x-\frac{x^{2}}{2}-\frac{\pi x^{2}}{8}\)
(iii) (c) : We have, \(A=5 x-\frac{x^{2}}{2}-\frac{\pi x^{2}}{8}\)
\(\Rightarrow \quad \frac{d A}{d x}=5-x-\frac{\pi x}{4}\)
Now, \(\frac{d A}{d x}=0 \Rightarrow 5=x+\frac{\pi x}{4}\)
\(\Rightarrow x(4+\pi)=20 \Rightarrow x=\frac{20}{4+\pi}\)
\(\left[\text { Clearly, } \frac{d^{2} A}{d x^{2}}<0 \text { at } x=\frac{20}{4+\pi}\right]\)
(iv) (d) : At \(x=\frac{20}{4+\pi}\)
\(A=5\left(\frac{20}{4+\pi}\right)-\left(\frac{20}{4+\pi}\right)^{2} \frac{1}{2}-\frac{\pi}{8}\left(\frac{20}{4+\pi}\right)^{2}\)
\(=\frac{100}{4+\pi}-\frac{200}{(4+\pi)^{2}}-\frac{50 \pi}{(4+\pi)^{2}}\)
\(=\frac{(4+\pi)(100)-200-50 \pi}{(4+\pi)^{2}}=\frac{400+100 \pi-200-50 \pi}{(4+\pi)^{2}}\)
\(=\frac{200+50 \pi}{(4+\pi)^{2}}=\frac{50(4+\pi)}{(4+\pi)^{2}}=\frac{50}{4+\pi}\)
(v) (a) : We have, \(y=5-\frac{x}{2}-\frac{\pi x}{4}=5-x\left(\frac{1}{2}+\frac{\pi}{4}\right)\)
\(=5-x\left(\frac{2+\pi}{4}\right)=5-\left(\frac{20}{4+\pi}\right)\left(\frac{2+\pi}{4}\right)\)
\(=5-5 \frac{(2+\pi)}{4+\pi}=\frac{20+5 \pi-10-5 \pi}{4+\pi}=\frac{10}{4+\pi}\) -
Let A be the event that the student is selected for LIC AAO, B be the event that the student is selected for SSC CGL and C be the event that the student is selected for Bank P.O.
Then, P(A) = a; P(B) = band P(C) = c
(i) (b): We have, \(P(A \cup B \cup C)=0.5\)
\(\Rightarrow \ 1-P(\overline{A \cup B \cup C})=0.5 \)
\(\Rightarrow 1-P(\bar{A} \cap \bar{B} \cap \bar{C})=0.5 \)
\(\Rightarrow 1-P(\bar{A}) \cdot P(\bar{B}) \cdot P(\bar{C})=0.5 \)
\(\Rightarrow\) 1 - (I - a) (1 - b) (1 - c) = 0.5
\(\Rightarrow\) 1 - [ (I - a - b + ab )(1 - c)] = 0.5
\(\Rightarrow\) 1 - [1 - c - a + ac - b + bc + ab - abc] = 0.5
\(\Rightarrow\) a + b + c - ab - bc - ca + abc = 0.5 .......(i)
(ii) (c): We have, P(selection in at least two competitive exams) = 0.4
\( \Rightarrow \ P(A \cap B \cap \bar{C})+P(\bar{A} \cap B \cap C)+P(A \cap \bar{B} \cap C)+ P(A \cap B \cap C)=0.4 \)
\(\Rightarrow\) ab(1 - c) + (1 - a)bc + a(1 - b)c + abc = 0.4
\(\Rightarrow\) ab - abc + bc - abc + ac - abc + abc = 0.4
\(\Rightarrow\) ab + bc + ac - 2abc= 0.4 ......................(ii)
(iii) (a) : We have, P(selection in exactly two examinations) = 0.3
\(\Rightarrow P(A \cap B \cap \bar{C})+P(\bar{A} \cap B \cap C)+P(A \cap \bar{B} \cap C)=0.3\)
\(\Rightarrow\) ab(1 - c) + (1 - a)bc + a(1 - b)c = 0.3
\(\Rightarrow\) ab + bc + ac - 3abc = 0.3 ...................(iii)
On subtracting (iii) from (ii), we get
abc = 0.1
(iv) (b): On substituting the value of abe in (ii), we get
ab + bc + ac = 0.6
(v) (a): On substituting the value of ab + bc + ac and
abc in (i), we get
a + b + c - 0.6 + 0.1 = 0.5
\(\Rightarrow\) a + b + c = 1 -
Here, \(\left|\vec{F}_{1}\right|=\sqrt{(4)^{2}+0^{2}}=4 \mathrm{KN}\)
\( \left|\vec{F}_{2}\right|=\sqrt{(-2)^{2}+4^{2}}=\sqrt{20} \mathrm{KN} \)
\(\left|\vec{F}_{3}\right|=\sqrt{(-3)^{2}+(-3)^{2}}=\sqrt{18} \mathrm{KN}\)
(i) (a): Since, \(\sqrt 20\) is larger. So, team B will win the game.
(ii) (b): Let F be the combined force
\(\therefore \vec{F}=\vec{F}_{1}+\vec{F}_{2}+\vec{F}_{3}=4 \hat{i}+0 \hat{j}-3 \hat{i}-3 \hat{j}-2 \hat{i}+4 \hat{j} \)
\(=-\hat{i}+\hat{j} \)
\(\therefore |\vec{F}|=\sqrt{(-1)^{2}+1^{2}}=\sqrt{2}=1.4 \mathrm{KN}\)
(iii) (c) : We have, \(\vec{F}=-\hat{i}+\hat{j}\)
\(\therefore \theta=\tan ^{-1}\left(\frac{F_{y}}{F_{x}}\right)=\tan ^{-1}\left(\frac{1}{-1}\right)=\frac{3 \pi}{4} \text { radian }\)
= 0.75 x 3.14 radian = 2.3555 radian ≈ 2.4 radian
(iv) (a): Magnitude of force of Team B = \(\sqrt 20\) KN
= 2\(\sqrt 5\) KN
(v) (b): 4 KN force is applied by team A. -
(i) (b): P(X = 2) = (Probability of not getting six at first throw) \(\times\) (Probability of getting six at second throw)
\(=\frac{5}{6} \times \frac{1}{6}=\frac{5}{6^{2}}\)
(ii) (c): P(X =4) = \(\frac{5}{6} \times \frac{5}{6} \times \frac{5}{6} \times \frac{1}{6}=\frac{5^{3}}{6^{4}}\)
(iii) (c) : P(X ≥ 2) = 1 - P(X < 2)
\(=1-P(X=1)=1-\frac{1}{6}=\frac{5}{6}\)
(iv) (a): \(P(X \geq 6)=\left(\frac{5}{6}\right)^{5} \times \frac{1}{6}+\left(\frac{5}{6}\right)^{6} \times \frac{1}{6}+\ldots \infty\)
\(=\frac{5^{5}}{6^{6}}\left[1+\frac{5}{6}+\left(\frac{5}{6}\right)^{2}+\ldots \infty\right]=\frac{5^{5}}{6^{6}}\left[\frac{1}{1-\frac{5}{6}}\right]=\left(\frac{5}{6}\right)^{5}\)
(v) (d): \(P(X \geq 4)=\left(\frac{5}{6}\right) \cdot \frac{1}{6}+\left(\frac{5}{6}\right)^{4} \cdot \frac{1}{6}+\ldots \ldots\)
\( =\frac{5^{3}}{6^{4}}\left[1+\left(\frac{5}{6}\right)+\left(\frac{5}{6}\right)^{2}+\ldots . .\right] \)
\(=\frac{5^{3}}{6^{4}}\left[\frac{1}{1-\left(\frac{5}{6}\right)}\right]=\left(\frac{5^{3}}{6^{4}}\right) \cdot 6=\frac{5^{3}}{6^{3}}\) -
(i) (b): Here (5, 3) are the coordinates of B.
\(\therefore\) P.V. of B = \(5 \hat{i}+3 \hat{j}\)
(ii) (d) : Here (9, 8) are the coordinates of D.
\(\therefore\) P.V. of D = \({9} \hat{i}+8 \hat{j}\)
(iii) (b) : P.V. of B = \(5 \hat{i}+3 \hat{j}\) and ஃ P.V. of C = \(6 \hat{i}+5 \hat{j}\)
\(\therefore \ \overrightarrow{B C}=(6-5) \hat{i}+(5-3) \hat{j}=\hat{i}+2 \hat{j}\)
(iv) (b): Since P.V. of A = \(2 \hat{i}+2 \hat{j}\) , P.V. of D = \({9} \hat{i}+8 \hat{j}\)
\( \therefore \overrightarrow{A D}=(9-2) \hat{i}+(8-2) \hat{j}=7 \hat{i}+6 \hat{j} \)
\(|\overrightarrow{A D}|^{2}=7^{2}+6^{2}=49+36=85 \)
\(\Rightarrow |\overrightarrow{A D}|=\sqrt{85} \text { units }\)
(v) (a): We have, \(\vec{M}=4 \hat{j}+3 \hat{k}\) ,
\( \therefore |\vec{M}|=\sqrt{4^{2}+3^{2}}=\sqrt{16+9}=\sqrt{25}=5 \)
\(\therefore \hat{M}=\frac{\vec{M}}{|\vec{M}|}=\frac{4 \hat{j}+3 \hat{k}}{5}=\frac{4}{5} \hat{j}+\frac{3}{5} \hat{k}\) -
(i) (d) : Line x + y = 3 cuts the x-axis and y-axis at (3, 0) and (0, 3) respectively
[Since, at x-axis, y = 0 and at y-axis, x = 0]
(ii) (c) : We have, y2 = 4x and x + y = 3
From (i) and (ii), we have y2 = 4(3 - y)
\(\Rightarrow y^{2}+4 y-12=0 \Rightarrow y^{2}+6 y-2 y-12=0\)
\(\Rightarrow y(y+6)-2(y+6)=0\)
\(\Rightarrow (y+6)(y-2)=0 \Rightarrow y=2, y=-6\)
From (ii), x = 3 - 2 = 1 or x = 3 + 6 = 9
\(\therefore\) Required points of intersection are (1, 2), (9, - 6)
(iii) (b) :
(iv) (d): \(\int_{-6}^{2}(3-y) d y=\left[3 y-\frac{y^{2}}{2}\right]_{-6}^{2}\)
\(=\left[6-\frac{4}{2}-\left[3(-6)-\frac{(-6)^{2}}{2}\right]\right]=4+36=40\)
(v) (c): Required area = \(\int_{-6}^{2}(3-y) d y-\int_{-6}^{2} \frac{y^{2}}{4} d y\)
\(=40-\frac{1}{4}\left[\frac{y^{3}}{3}\right]_{-6}^{2}=40-\frac{1}{4}\left[\frac{8}{3}-\frac{(-6)^{3}}{3}\right]\)
\(=40-\frac{2}{3}-\frac{216}{12}=\frac{480-8-216}{12}=\frac{256}{12}=\frac{64}{3} \mathrm{sq} . \text { units }\) -
(i) (a) : Equation of line AB is
\(y-0=\frac{3-0}{1+1}(x+1) \Rightarrow y=\frac{3}{2}(x+1)\)
(ii) (c) : Equation of line BC is \(y-3=\frac{2-3}{3-1}(x-1)\)
\(\Rightarrow y=-\frac{1}{2} x+\frac{1}{2}+3 \Rightarrow y=\frac{-1}{2} x+\frac{7}{2}\)
(iii) (d) : Area of region ABCD
= Area of \(\triangle A B E\) + Area of region BCDE
\(=\int_{-1}^{1} \frac{3}{2}(x+1) d x+\int_{1}^{3}\left(\frac{-1}{2} x+\frac{7}{2}\right) d x\)
\(=\frac{3}{2}\left[\frac{x^{2}}{2}+x\right]_{-1}^{1}+\left[\frac{-x^{2}}{4}+\frac{7}{2} x\right]_{1}^{3}\)
\(=\frac{3}{2}\left[\frac{1}{2}+1-\frac{1}{2}+1\right]+\left[\frac{-9}{4}+\frac{21}{2}+\frac{1}{4}-\frac{7}{2}\right]\)
= 3 + 5 = 8 sq. units
(iv) (a) : Equation of line AC is \(y-0=\frac{2-0}{3+1}(x+1)\)
\(\Rightarrow y=\frac{1}{2}(x+1)\)
\(\therefore \text { Area of } \Delta A D C=\int_{-1}^{3} \frac{1}{2}(x+1) d x=\left[\frac{x^{2}}{4}+\frac{1}{2} x\right]_{-1}^{3}\)
\(=\frac{9}{4}+\frac{3}{2}-\frac{1}{4}+\frac{1}{2}=4 \text { sq. units }\)
(v) (b) : Area of \(\Delta A B C\)= Area of region ABCD - Area of \(\Delta A C D=8-4=4 \mathrm{sq} . \text { units }\) -
(i) (a) : \(\vec{a}=\hat{i}+4 \hat{j}+2 \hat{k}, \vec{b}=3 \hat{i}-3 \hat{j}-2 \hat{k}\) and \(\vec{c}=-2 \hat{i}+2 \hat{j}+6 \hat{k}\)
\(\therefore \ \vec{a}+\vec{b}+\vec{c}=2 \hat{i}+3 \hat{j}+6 \hat{k}\)
(ii) (c): Using triangle law of addition in \(\Delta\)ABC, we get
\(\overrightarrow{A B}+\overrightarrow{B C}+\overrightarrow{C A}=\overrightarrow{0}\) which can be rewritten as
\(\overrightarrow{A B}+\overrightarrow{B C}-\overrightarrow{A C}=\overrightarrow{0} \text { or } \overrightarrow{A B}-\overrightarrow{C B}+\overrightarrow{C A}=\overrightarrow{0}\)
(iii) (c) : We have, A(1, 4, 2), B(3, -3, -2) and C(-2, 2, 6)
Now, \(\overrightarrow{A B}=\vec{b}-\vec{a}=2 \hat{i}-7 \hat{j}-4 \hat{k}\)
and \(\overrightarrow{A C}=\vec{c}-\vec{a}=-3 \hat{i}-2 \hat{j}+4 \hat{k}\)
\(\therefore \overrightarrow{A B} \times \overrightarrow{A C}=\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 2 & -7 & -4 \\ -3 & -2 & 4 \end{array}\right|\)
\(=\hat{i}(-28-8)-\hat{j}(8-12)+\hat{k}(-4-21)=-36 \hat{i}+4 \hat{j}-25 \hat{k}\)
Now, \(|\overrightarrow{A B} \times \overrightarrow{A C}|=\sqrt{(-36)^{2}+4^{2}+(-25)^{2}}\)
\(=\sqrt{1296+16+625}=\sqrt{1937}\)
\(\therefore \text { Area of } \Delta A B C=\frac{1}{2}|\overrightarrow{A B} \times \overrightarrow{A C}|=\frac{1}{2} \sqrt{1937} \text { sq. units }\)
(iv) (d): If the given points lie on the straight line, then the points will be collinear and so area of \( \Delta A B C=0 \)
\(\Rightarrow |\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}|=0\)
If a, b, c are the position vectors of the three vertices A, Band C of \( \Delta A B C \), then area of triangle
\(\left.=\frac{1}{2}|\vec{a} \times \vec{b}+\vec{b} \times \vec{c}+\vec{c} \times \vec{a}|\right]\)
(v) (b): Here, \( |\vec{a}| =\sqrt{2^{2}+3^{2}+6^{2}}=\sqrt{4+9+36} \)
\(=\sqrt{49}=7\)
\(\therefore\) Unit vector in the direction of vector \(\vec{a}\) is
\(\hat{a}=\frac{2 \hat{i}+3 \hat{j}+6 \hat{k}}{7}=\frac{2}{7} \hat{i}+\frac{3}{7} \hat{j}+\frac{6}{7} \hat{k}\) -
(i) (c): Clearly, the plane for students of school A is \(\vec{r} \cdot(\hat{i}+\hat{j}+2 \hat{k})=5,\) which can be rewritten as
\((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(\hat{i}+\hat{j}+2 \hat{k})=5\)
\(\Rightarrow \quad x+y+2 z=5\), which is the required cartesian equation.
(ii) (b): Clearly, the equation of plane for students of school B is \(\vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})=6,\) which is of the form \(\vec{r} \cdot \vec{n}=d\)
∴ Normal vector to the plane is, \(\vec{n}=2 \hat{i}-\hat{j}+\hat{k}\) and its magnitude is \(|\vec{n}|=\sqrt{2^{2}+(-1)^{2}+1^{2}}=\sqrt{6}\)
(iii) (b): The cartesian form is 2x - y + z = 6, which can be rewritten as
\(\frac{2 x}{6}-\frac{y}{6}+\frac{z}{6}=1 \Rightarrow \frac{x}{3}+\frac{y}{(-6)}+\frac{z}{6}=1\)
(iv) (c): Since, only the point (3, I, 1) satisfy the equation of plane representing seating position of students of school B, therefore Khushi is the student of school B.
(v) (d): Equation of plane representing students of school B is \(\vec{r} \cdot(2 \hat{i}-\hat{j}+\hat{k})=6,\) which is not in normal form, as \(|\vec{n}| \neq 1\)
On dividing both sides by \(\sqrt{2^{2}+(-1)^{2}+1^{2}}=\sqrt{6}\), we get \(\vec{r} \cdot\left(\frac{2}{\sqrt{6}} \hat{i}-\frac{1}{\sqrt{6}} \hat{j}+\frac{1}{\sqrt{6}} \hat{k}\right)=\frac{6}{\sqrt{6}}\)
which is of the form \(\vec{r} \cdot \hat{n}=d\)
Thus, the required distance is \(\sqrt 6\) units. -
(i) b : Curves y = cos x and y = x + 1 meet at point C(O, 1).
(ii) C : curve y=cosx meet the x axis at \(A^{\prime}\left(\frac{-\pi}{2}, 0\right)\) and \(A\left(\frac{\pi}{2}, 0\right)\) .
(iii) (a) : \(\int_{-1}^{0}(x+1) d x=\left[\frac{x^{2}}{2}+x\right]_{-1}^{0}=0-\left(\frac{1}{2}-1\right)=\frac{1}{2}\)
(iv) (d) : \(\int_{0}^{\pi / 2} \cos x d x=[\sin x]_{0}^{\pi / 2}=\sin \frac{\pi}{2}-\sin 0=1\)
(v) (b) : Required area \(\int_{-1}^{0}(x+1) d x+\int_{0}^{\pi / 2} \cos x d x\)
\(=\frac{1}{2}+1=\frac{3}{2} \text { sq. units }\) -
(i) (b) : Equation of plane is x - 2y + 2z = 3
∴ D.R's of normal to the plane are < 1, - 2, 2 >, which is also the D.R.'s of perpendicular from the point (3, -2, 1) to the given plane.
(ii) (c) : Required length = Perpendicular distance from (3, -2, 1) to the plane x - 2y + 2z = 3
\(=\left|\frac{3-2(-2)+2(1)-3}{\sqrt{1^{2}+(-2)^{2}+2^{2}}}\right|=\frac{6}{3}=2 \text { units }\)
(iii) (b) : The equation of perpendicular from the point (x1, y1, z1) to the plane ax + by + cz = d is given by
\(\frac{x-x_{1}}{a}=\frac{y-y_{1}}{b}=\frac{z-z_{1}}{c}\)
Here, x1 = 3, y1 = -2, z1= 1 and a = 1, b = -2, c = 2
∴ Required equation is \(\frac{x-3}{1}=\frac{y+2}{-2}=\frac{z-1}{2}\)
(iv) (d) : The equation of the plane parallel to the plane x - 2y + 2z - 3 = 0 is x - 2y + 2z + \(\lambda\) = 0
Now, distance of this plane from the point (3, -2, 1) is
\(\left|\frac{3+4+2+\lambda}{\sqrt{1^{2}+(-2)^{2}+2^{2}}}\right|=\left|\frac{9+\lambda}{3}\right|\)
But, this distance is given to be unity
\(\therefore|9+\lambda|=3 \Rightarrow \lambda+9=\pm 3 \Rightarrow \lambda=-6 \text { or }-12\)
Thus, required equation of planes are
x - 2y + 2z - 6 = 0 or x- 2y + 2z - 12 = 0
(v) (a): Let the coordinate of image of (3, -2, 1) be Q(r + 3, -2r - 2, 2r + 1)
Let R be the mid-point of PQ, then coordinate of R be \(\left(\frac{r+6}{2}, \frac{-2 r-4}{2}, r+1\right)\)
Since, R lies on the plane x - 2y + 2z = 3
\( \therefore \quad\left(\frac{r+6}{2}\right)-2\left(\frac{-2 r-4}{2}\right)+2(r+1)=3 \)
\(\Rightarrow \quad 9 r=-12 \Rightarrow r=-\frac{4}{3}\)
Thus, the coordinates of Q be \(\left(\frac{5}{3}, \frac{2}{3}, \frac{-5}{3}\right)\) -
(i) (d) :Given, at any time t the thermometer reading be ToF and the outside temperature be sop.
Then, by Newton's law of cooling, we have
\(\frac{d T}{d t} \propto(T-S) \Rightarrow \frac{d T}{d t}=-\lambda(T-S)\)
(ii) (d) : Since, after 5 minutes, thermometer reads 600F.
\(\therefore\) Value of T(5) = 600F
(iii) (a) : Clearly from given information, value of T( 10) is 50°F.
(iv) (b) : We have,\(\frac{d T}{d t}=-\lambda(T-S)\)
\(\Rightarrow \frac{d T}{T-S}=-\lambda d t \Rightarrow \int \frac{1}{T-S} d T=-\lambda \int d t\)
\(\Rightarrow \log (T-S)=-\lambda t+c\)
(v) (c) : Since, at t = 0, T = 80°
Case Study Questions






































