CBSE 12th Standard Maths Subject Case Study Questions With Solution 2021 Part - II
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 12 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Maths Subject Case Study Questions With Solution 2021 Part - II
12th Standard CBSE
-
Reg.No. :
Maths
-
Three car dealers, say A, Band C, deals in three types of cars, namely Hatchback cars, Sedan cars, SUV cars. The sales figure of 2019 and 2020 showed that dealer A sold 120 Hatchback, 50 Sedan, 10 SUV cars in 2019 and 300 Hatchback, 150 Sedan, 20 SUV cars in 2020; dealer B sold 100 Hatchback, 30 Sedan,S SUV cars in 2019 and 200 Hatchback, 50 Sedan, 6 SUV cars in 2020; dealer C sold 90 Hatchback, 40 Sedan, 2 SUV cars in 2019 and 100 Hatchback, 60 Sedan,S SUV cars in 2020.
Based on the above information, answer the following questions.
(i) The matrix summarizing sales data of 2019 is
(ii) The matrix summarizing sales data of 2020 is
(iii) The total number of cars sold in two given years, by each dealer, is given by the matrix
(iv) The increase in sales from 2019 to 2020 is given by the matrix
(v) If each dealer receive profit of Rs. 50000 on sale of a Hatchback, Rs. 100000 on sale of a Sedan and Rs. 200000 on sale of a SUV (v) then amount of profit received in the year 2020 by each dealer is given by the matrix.
(a) -
Three schools A, Band C organized a mela for collecting funds for helping the rehabilitation of flood victims. They sold hand made fans, mats and plates from recycled material at a cost of Rs. 25, Rs.100 and Rs.50 each. The number of articles sold by school A, B, C are given below.
Artilcle\School A B C Fans 40 25 35 Mats 50 40 50 Plates 20 30 40 Based on above information, answer the following questions.
(i) If P be a 3 x 3 matrix represent the sale of handmade fans, mats and plates by three schools A, Band C, then
(ii) If Q be a 3 x 1 matrix represent the sale prices (in Rs) of given products per unit, then
(iii) The funds collected by school A by selling the given articles is(a) Rs. 7000 (b) Rs. 6125 (c) Rs. 7875 (d) Rs. 8000 (iv) The funds collected by school B by selling the given articles is
(a) Rs. 5125 (b) Rs. 6125 (c) Rs. 7125 (d) Rs. 8125 (v) The total funds collected for the required purpose is
(a) Rs. 20000 (b) Rs. 21000 (c) Rs. 30000 (d) Rs. 35000 (a) -
The upward speed v(t) of a rocket at time t is approximated by \(\begin{equation} v(t)=a t^{2}+b t+c, 0 \leq t \leq 100 \end{equation}\) ,where a, band c are constants. It has been found that the speed at times t = 3, t = 6 and t = 9 seconds are respectively 64, 133 and 208 miles per second.
If \(\begin{equation} \left(\begin{array}{ccc} 9 & 3 & 1 \\ 36 & 6 & 1 \\ 81 & 9 & 1 \end{array}\right)^{-1}=\frac{1}{18}\left(\begin{array}{ccc} 1 & -2 & 1 \\ -15 & 24 & -9 \\ 54 & -54 & 18 \end{array}\right) \end{equation}\) ,then answer the following questions
(i) The value of b + c is(a) 20 (b) 21 (c) 3/4 (d) 4/3 (ii) The value of a + c is
(a) 1 (b) 20 (c) 4/3 (d) none of these (iii) v(t) is given by
(a) t2+20t+l (b) \(\begin{equation} \frac{1}{3} t^{2}+20 t+1 \end{equation}\) (c) \(\begin{equation} t^{2}+\frac{1}{3} t+20 \end{equation}\) (d) P + t + 1 (iv) The speed at time t = 15 seconds is
(a) 346 miles/see (b) 356 miles/see (c) 366 miles/see (d) 376 miles/see (v) The time at which the speed of rocket is 784 miles/see is
(a) 20 seconds (b) 30 seconds (c) 25 seconds (d) 27 seconds (a) -
Minor of an element aij of a determinant is the determinant obtained by deleting its ith row and /h column in aij lies and is denoted by Mij.
Cofactor of an element aij'denoted by Aij,is defined by \(\begin{equation} A_{i j}=(-1)^{i+j} M_{i j} \end{equation}\), where Mij is minor of aij.
Also, the determinant of a square matrix A is the sum of the products of the elements of any row (or column with their corresponding cofactors.
For example if \(\begin{equation} A=\left[a_{i j}\right]_{3 \times 3}, \text { then }|A|=a_{11} A_{11}+a_{12} A_{12}+a_{13} A_{13} \end{equation}\) .
Based on the above information, answer the following questions
(i) Find the sum of the cofactors of all the elements of \(\begin{equation} \left|\begin{array}{cc} 1 & -2 \\ 4 & 3 \end{array}\right| \end{equation}\)(a) 1 (b) -2 (c) 4 (d) 1 (ii) Find the minor of a21 of \(\begin{equation} \left|\begin{array}{ccc} 5 & 6 & -3 \\ -4 & 3 & 2 \\ -4 & -7 & 3 \end{array}\right| \end{equation}\)
(a) 3 (b) -3 (c) 39 (d) -39 (iii) In the determinant \(\begin{equation} \left|\begin{array}{ccc} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{array}\right| \end{equation}\) find the value of a32·A32
(a) 27 (b) -110 (c) 110 (d) -27 (iv) If \(\begin{equation} \Delta=\left|\begin{array}{lll} 5 & 3 & 8 \\ 2 & 0 & 1 \\ 1 & 2 & 3 \end{array}\right| \end{equation}\), find the value of a32·A32 .
(a) -10 (b) -7 (c) 10 (d) 7 (v) If \(\begin{equation} \Delta=\left|\begin{array}{ccc} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{array}\right| \end{equation}\), then find the value of \(\begin{equation} |\Delta| \end{equation}\).
(a) 26 (b)28 (c) 72 (d) 46 (a) -
If a real valued function f(x) is finitely derivable at any point of its domain, it is necessarily continuous at that point. But its converse need not be true.
For example, every polynomial. constant function are both continuous as well as differentiable and inverse trigonometric functions are continuous and differentiable in its domains etc.
Based on the above information, answer the following questions.
(i) If \(\begin{equation} f(x)=\left\{\begin{array}{l} x, \text { for } x \leq 0 \\ 0, \text { for } x>0 \end{array}\right. \end{equation}\) , then at x = 0(a) f(x) is differentiable and continuous (b) j(x) is neither continuous nor differentiable (c) f(x) is continuous but not differentiable (d) none of these (ii) If \(\begin{equation} f(x)=|x-1|, x \in R \end{equation}\) ,then at x= 1
(a) f(x) is not continuous (b) f(x) is continuous but not differentiable (c) f(x) is continuous and differentiable (d) none of these (iii) f(x) = x3 is
(a) continuous but not differentiable at x = 3 (b) continuous and differentiable at x = 3 (c) neither continuous nor differentiable at x = 3 (d) none of these (iv) f(x) = [sin x], then which of the following is true?
(a) j(x) is continuous and differentiable at x = o. (b) j(x) is discontinuous at x = o. (c) j(x) is continuous at x = 0 but not differentiable (d) fix) is differentiable but not continuous at \(\begin{equation} x=\pi / 2 \end{equation}\) (v) If f(x) = sin-1x, \(\begin{equation} -1 \leq x \leq 1 \end{equation}\), then
(a) f(x) is both continuous and differentiable (b) f(x) is neither continuous nor differentiable. (c) f(x) is continuous but not differentiable (d) None of these (a) -
If a relation between x and y is such that y cannot be expressed in terms of x, then y is called an implicit function of x.
When a given relation expresses y as an implicit function of x and we want to find \(\begin{equation} \frac{d y}{d x} \end{equation}\).then
we differentiate every term of the given relation w.r.t. x. remembering that a term in y is first differentiated w.r.t. y and then multiplied by \(\begin{equation} \frac{d y}{d x} \end{equation}\).
Based on the above information, find the value of \(\begin{equation} \frac{d y}{d x} \end{equation}\) in each of the following questions
(i) x3+x2y+xy2+y3=81(a) \(\begin{equation} \frac{\left(3 x^{2}+2 x y+y^{2}\right)}{x^{2}+2 x y+3 y^{2}} \end{equation}\) (b) \(\begin{equation} \frac{-\left(3 x^{2}+2 x y+y^{2}\right)}{x^{2}+2 x y+3 y^{2}} \end{equation}\) (c) \(\begin{equation} \frac{\left(3 x^{2}+2 x y-y^{2}\right)}{x^{2}-2 x y+3 y^{2}} \end{equation}\) (d) \(\begin{equation} \frac{3 x^{2}+x y+y^{2}}{x^{2}+x y+3 y^{2}} \end{equation}\) (ii) xy = c- y
(a) \(\begin{equation} \frac{x-y}{(1+\log x)} \end{equation}\) (b) \(\begin{equation} \frac{x+y}{(1+\log x)} \end{equation}\) (c) \(\begin{equation} \frac{x-y}{x(1+\log x)} \end{equation}\) (d) \(\begin{equation} \frac{x+y}{x(1+\log x)} \end{equation}\) (iii) esiny = xy
(a) \(\begin{equation} \frac{-y}{x(y \cos y-1)} \end{equation}\) (b) \(\begin{equation} \frac{y}{y \cos y-1} \end{equation}\) (c) \(\begin{equation} \frac{y}{y \cos y+1} \end{equation}\) (d) \(\begin{equation} \frac{y}{x(y \cos y-1)} \end{equation}\) (iv) sin2 x + cos2y = 1
(a) \(\begin{equation} \frac{\sin 2 y}{\sin 2 x} \end{equation}\) (b) \(\begin{equation} -\frac{\sin 2 x}{\sin 2 y} \end{equation}\) (c) \(\begin{equation} -\frac{\sin 2 y}{\sin 2 x} \end{equation}\) (d) \(\begin{equation} \frac{\sin 2 x}{\sin 2 y} \end{equation}\) (v) \(\begin{equation} y=(\sqrt{x})^{\sqrt{x}} \end{equation}\)
(a) \(\begin{equation} \frac{-y^{2}}{x(2-y \log x)} \end{equation}\) (b) \(\begin{equation} \frac{y^{2}}{2+y \log x} \end{equation}\) (c) \(\begin{equation} \frac{y^{2}}{x(2+y \log x)} \end{equation}\) (d) \(\begin{equation} \frac{y^{2}}{x(2-y \log x)} \end{equation}\) (a) -
The Government declare that farmers can get Rs.300 per quintal for their onions on 1st July and after that,the price will be dropped by Rs. 3 per quintal per extra day.
Shyams father has 80 quintal of onions in the field on 1st July and he estimates that crop is increasing at the rate of 1 quintal per day.
Based on the above information, answer the following questions.
(i) If x is the number of days after 1st July, then price and quantity ofonion respectively can be expressed as(a) Rs. (300 - 3x), (80 + x) quintals (b) Rs. (300 - 3x), (80 - x) quintals (c) Rs. (300 + x), 80 quintals (d) None of these (ii) Revenue R as a function of x can be represented as
(a) R(x) = 3x2 - 60x - 24000 (b) R(x) = -3x2 + 60x + 24000 (c) R(x) = 3x2 + 40x - 16000 (d) R(x) = 3x2- 60x - 14000 (iii) Find the number of days after 1stJuly, when Shyams father attain maximum revenue.
(a) 10 (b) 20 (c) 12 (d) 22 (iv) On which day should Shyam's father harvest the onions to maximise his revenue?
(a) 11thuly (b) 20th July (c) 12th July (d) 22nd July (v) Maximum revenue is equal to
(a) Rs. 20,000 (b) Rs. 24,000 (c) Rs. 24,300 (d) Rs. 24,700 (a) -
Linear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations.
Based on the above information, answer the following questions.
(i) The optimal value of the objective function is attained at the points(a) on X-axis (b) on Y-axis (c) which are corner points of the feasible region (d) none of these (ii) The graph of the inequality 3x + 4y < 12 is
(a) half plane that contains the origin (b) half plane that neither contains the origin nor the points of the line 3x + 4y =12. (c) whole XOY-plane excluding the points on line 3x + 4y = 12 (d) none of these (iii) The feasible region for an LPP is shown in the figure. Let Z = 2x + 5y be the objective function. Maximum of Z occurs at
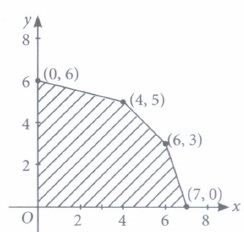
(a) (7,0) (b) (6,3) (c) (0,6) (d) (4,5) (iv) The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is
(a) p = q (b) p = 2q (c) q=2p (d) q=3p (v) The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20,40), (60,20), (60, 0). The objective function is Z = 4x + 3y. Compare the quantity in Column A and Column B
Column A Column B Maximum of Z 325 (a) The quantity in column A is greater (b) The quantity in column B is greater (c) The two quantities are equal (d) The relationship cannot be determined on the basis of the information supplied (a) -
A tin can manufacturer designs a cylindrical tin can for a company making sanitizer and disinfector. The tin can is made to hold 3 litres of sanitizer or disinfector.
Based on the above in formation, answer the following questions.
(i) If r cm be the radius and h em be the height of the cylindrical tin can, then the surface area expressed as a function of r as(a) \(2 \pi r^{2}\) (b) \(\sqrt{\frac{500}{\pi}} \mathrm{cm}\) (c) \(\sqrt[3]{\frac{1500}{\pi}} \mathrm{cm}\) (d) \(2 \pi r^{2}+\frac{6000}{r}\) (ii) The radius that will minimize the cost of the material to manufacture the tin can is
(a) \(\sqrt[3]{\frac{600}{\pi}} \mathrm{cm}\) (b) \(\sqrt{\frac{500}{\pi}} \mathrm{cm}\) (c) \(\sqrt[3]{\frac{1500}{\pi}} \mathrm{cm}\) (d) \(\sqrt{\frac{1500}{\pi}} \mathrm{cm}\) (iii) The height thatt will minimize the cost of the material to manufacture the tin can is
(a) \(\sqrt[3]{\frac{1500}{\pi}} \mathrm{cm}\) (b) \(2 \sqrt[3]{\frac{1500}{\pi}} \mathrm{cm}\) (c) \(\sqrt{\frac{1500}{\pi}}\) (d) \(2 \sqrt{\frac{1500}{\pi}}\) (iv) If the cost of material used to manufacture the tin can is Rs.100/m2 and \(\sqrt[3]{\frac{1500}{\pi}} \approx 7.8\) then minimum cost is approximately
(a) Rs. 11.538 (b) Rs. 12 (c) Rs. 13 (d) Rs. 14 (v) To minimize the cost of the material used to manufacture the tin can, we need to minimize the
(a) volume (b) curved surface area (c) total surface area (d) surface area of the base (a) -
Suppose a dealer in rural area wishes to purpose a number of sewing machines. He has only Rs. 5760 to invest and has space for at most 20 items for storage. An electronic sewing machine costs him Rs. 360 and a manually operated sewing machine Rs. 240. He can sell an electronic sewing machine at a profit of Rs. 22 and a manually operated sewing machine at a profit of Rs. 18.
Based on the above information, answer the following questions.
(i) Let x and y denotes the number of electronic sewing machines and manually operated sewing machines purchased by the dealer. If it is assume that the dealer purchased atleast one of the given machines, then(a) x + y ≥ 0 (b) x + y < 0 (c) x + y > 0 (d) x + y ≤ 0 (ii) Let the constraints in the given problem is represented by the following inequalities
x + y ≤ 20
360x + 240y ≤ 5760
x, y ≥ 0
Then which of the following point lie in its feasible region.(a) (0, 24) (b) (8, 12) (c) (20, 2) (d) None of these (iii) If the objective function of the given problem is maximise z = 22x + 18y, then its optimal value occur at
(a) (0, 0) (b) (16, 0) (c) (8, 12) (d) (0, 20) (iv) Suppose the following shaded region APDO, represent the feasible region corresponding to mathematical formulation. of given problem. Then which of the following represent the coordinates of one of its corner points.
(a) (0, 24) (b) (12, 8) (c) (8, 12) (d) (6, 14) (v) If an LPP admits optimal solution at two consecutive vertices of a feasible region, then
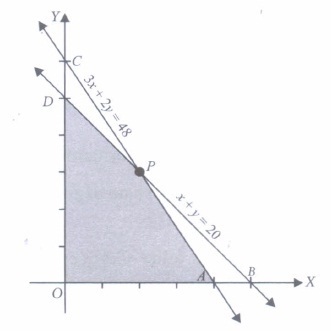
(a) the required optimal solution is at the midpoint of the line joining two points. (b) the optimal solution occurs at every point on the line joining these two points. (c) the LPP under consideration is not solvable. (d) the LPP under consideration must be reconstructed. (a) -
Nitin wants to construct a rectangular plastic tank for his house that can hold 80 ft 3 of water. The top of the tank is open. The width of tank will be 5 ft but the length and heights are variables. Building the tank cost Rs.20 per sq. foot for the base and Rs. 10 per square foot for the side.
Based on the above information, answer the following questions.(i) In order to make a least expensive water tank, Nitin need to minimize its
(a) Volume (b) Base (c) Curved surface area (d) Cost (ii) Total cost of tank as a function of h can' be' represented as
(a) c(h) = 100 h - 320 - 1600lh (b) (h) = 100 h - 320 h - 720 h2 (c) c(h) = 100 + 220 h + 1600 h2 (d) \(c(h)=100 h+320+\frac{1600}{h}\) (iii) Range of h is
(a) (3,5) (b) \((0, \infty)\) (c) (0,8) (d) (0,3) (iv) Value of h at which c(h) is minimum, is
(a) 4 (b) 5 (c) 6 (d) 6.7 (v) The cost ofleast expensive tank is
(a) Rs. 1020 (b) Rs. 1100 (c) Rs. 1120 (d) Rs. 1220 (a) -
A doctor is to visit a patient. From the past experience, it is known that the probabilities that he will come by cab, metro, bike or by other means of transport are respectively 0.3, 0.2, 0.1 and 0.4. The probabilities that he will be late are 0.25, 0.3, 0.35 and 0.1 if he comes by cab, metro, bike and other means of transport respectively.

Based on the above information, answer the following questions.
(i) When the doctor arrives late, what is the probability that he comes by metro?\((a) \ \frac{5}{4}\) \((b) \ \frac{2}{7}\) \((c) \ \frac{5}{21}\) \((d) \ \frac{1}{6}\) (ii) When the doctor arrives late, what is the probability that he comes by cab?
\((a) \ \frac{4}{21}\) \((b) \ \frac{1}{7}\) \((c) \ \frac{5}{14}\) \((d) \ \frac{2}{21}\) (iii) When the doctor arrives late, what is the probability that he comes by bike?
\((a) \ \frac{5}{21}\) \((b) \ \frac{4}{7}\) \((c) \ \frac{5}{6}\) \((d) \ \frac{1}{6}\) (iv) When the doctor arrives late, what is the probability that he comes by other means of transport?
\((a) \ \frac{6}{7}\) \((b) \ \frac{5}{14}\) \((c) \ \frac{4}{21}\) \((d) \ \frac{2}{7}\) (v) What is the probability that the doctor is late by any means?
\((a) \ 1\) \((b) \ 0\) \((c) \ \frac{1}{2}\) \((d) \ \frac{1}{4}\) (a) -
A card is lost from a pack of 52 cards. From the remaining cards two cards are drawn at random.

Based on the above information, answer the following questions.
(i) The probability of drawing two diamonds, given that a card of diamond is missing, isa) \(\frac{21}{425}\) (b) \(\frac{22}{425}\) (c) \(\frac{23}{425}\) (d) None of these (ii) The probability of drawing two diamonds, given that a card of heart is missing, is
a) \(\frac{26}{425}\) (b) \(\frac{22}{425}\) (c) \(\frac{19}{425}\) (d) \(\frac{23}{425}\) (iii) Let A be the event of drawing two diamonds from remaining 51 cards and E1, E2, E3 and E4 be the events that lost card is of diamond, club, spade and heart respectively, then the approximate value of \(\sum_{i=1}^{4} P\left(A \mid E_{i}\right) \text { is }\)
a) 0.17 (b) 0.24 (c) 0.25 (d) 0.18 (iv) All of a sudden, missing card is found and, then two cards are drawn simultaneously without replacement. Probability that both drawn cards are king is
a) \(\frac{1}{52}\) (b) \(\frac{1}{221}\) (c) \(\frac{1}{121}\) (d) \(\frac{2}{221}\) (v) If two cards are drawn from a well shuffled pack of 52 cards, one by one with replacement, then probability of getting not a king in 1st and 2nd draw is
a) \(\frac{144}{169}\) (b) \(\frac{12}{169}\) (c) \(\frac{64}{169}\) (d) None of these (a) -
To teach the application of probability a maths teacher arranged a surprise game for 5 of his students namely Archit, Aadya, Mivaan, Deepak and Vrinda. He took a bowl containing tickets numbered 1 to 50 and told the students go one by one and draw two tickets simultaneously from the bowl and replace it after noting the numbers.

Based on the above information, answer the following questions
(i) Teacher ask Vrinda, what is the probability that both tickets drawn by Archit shows even number?(a) 1/50 (b) 12/49 (c) 13/49 (d) 15/49 (ii) Teacher ask Mivaan, what is the probability that both tickets drawn by Aadya shows odd number?
a) 1/50 (b) 2/49 (c) 12/49 (d) 5/49 (iii) Teacher ask Deepak, what is the probability that tickets drawn by Mivaan, shows a multiple of 4 on one ticket and a multiple 5 on other ticket?
a) 14/245 (b) 16/245 (c) 24/245 (d) None of these (iv) Teacher ask Archit, what is the probability that tickets are drawn by Deepak, shows a prime number on one ticket and a multiple of 4 on other ticket?
a) 3/245 (b) 17/245 (c) 18/245 (d) 36/245 (v) Teacher ask Aadya, what is the probability that tickets drawn by Vrinda, shows an even number on first ticket and an odd' number on second ticket?
a) 15/98 (b) 25/98 (c) 35/98 (d) none of these (a) -
A magazine company in a town has 5000 subscribers on its list and collects fix charges of Rs. 3000 per year from each subscriber. The company proposes to increase the annual charges and it is believed that for every increase of Rs. 1, one subscriber will discontinue service.
Based on the above information, answer the following questions.
(i) If x denote the amount of increase in annual charges, then revenue R, as a function of x can be represented as(a) R(x) = 3000 x 5000 x x (b) R(x) = (3000 - 2x) (5000 + 2x) (c) R(x) = (5000 + x) (3000 - x) (d) R(x) = (3000 + x) (5000 - x) (ii) If magazine company increases Rs.500 as annual charges, then R is equal to
(a) 400 (b) 1600 (c) Both (a) and (b) (d) None of these (iv) What amount of increase in annual charges will bring maximum revenue?
(a) Rs.1000 (b) Rs.2000 (c) Rs.3000 (d) Rs. 4000 (v) Maximum revenue is equal to
(a) Rs. 15000000 (b) Rs. 16000000 (c) Rs. 20500000 (d) Rs. 25000000 (a)
Case Study Questions
*****************************************
CBSE 12th Standard Maths Subject Case Study Questions With Solution 2021 Part - II Answer Keys
-
(i) (b) : In 2019,dealer A sold 120 Hatchback, 50 Sedan and 10 SUV; dealer B sold 100 Hatchback, 30 Sedan and 5 SUV and dealer C sold 90 Hatchback, 40 Sedan and 2 SUV
\(\therefore\) Required matrix, say P, is given by
(ii) (a) : In 2020,
dealer A sold 300 Hatchback, 150 Sedan, 20 SUV
dealer B sold 200 Hatchback, 50 sedan, 6 SUV
dealer C sold 100 Hatchback, 60 sedan,S SUV
\(\therefore\) Required matrix, say Q, is given by
(iii) (c) : Total number of cars sold in two given years, by each dealer, is given by
(iv) (c): The increase in sales from 2019 to 2020 is given by
(v) (c) : The amount of profit in 2020 received by each dealer is given by the matrix
\(\begin{array}{c} A \\ B \\ C \end{array}\left[\begin{array}{c} 15000000+15000000+4000000 \\ 10000000+5000000+1200000 \\ 5000000+6000000+1000000 \end{array}\right]\)
\(\begin{array}{r} A \\ =B \\ C \end{array}\left[\begin{array}{l} 34000000 \\ 16200000 \\ 12000000 \end{array}\right]\) -
(i) (a) : Clearly,
(ii) (d) : Since Q is a 3 x 1 matrix, therefore
(iii) (a) : Clearly, total funds collected by each school is given by the matrix.
\(P Q=\left[\begin{array}{ccc} 40 & 50 & 20 \\ 25 & 40 & 30 \\ 35 & 50 & 40 \end{array}\right]\left[\begin{array}{c} 25 \\ 100 \\ 50 \end{array}\right]\)
\(=\left[\begin{array}{c} 1000+5000+1000 \\ 625+4000+1500 \\ 875+5000+2000 \end{array}\right]=\left[\begin{array}{l} 7000 \\ 6125 \\ 7875 \end{array}\right]\)
\(\therefore\) Funds collected by school A is Rs. 7000
Funds collected by school B is Rs. 6125
Pimds collected by school C is Rs. 7875
(iv) (b)
(v) (b) : Total funds collected for the required purpose
= Rs. (7000 + 6125 + 7875) = Rs. 21000 -
Since v(3) = 64, v(6) = 133 and v(9) = 208, we get the following system of linear equations
9a + 3b + c = 64
36a + 6b + c = 133
81a + 9b + c = 208
This can be written in matrix form as
\(\begin{equation} \left[\begin{array}{ccc} 9 & 3 & 1 \\ 36 & 6 & 1 \\ 81 & 9 & 1 \end{array}\right]\left[\begin{array}{l} a \\ b \\ c \end{array}\right]=\left[\begin{array}{c} 64 \\ 133 \\ 208 \end{array}\right] \end{equation}\)
or AX = B
Since,\(\begin{equation} A^{-1}=\frac{1}{18}\left(\begin{array}{ccc} 1 & -2 & 1 \\ -15 & 24 & -9 \\ 54 & -54 & 18 \end{array}\right) \end{equation}\)
\(\begin{equation} \therefore \quad X=\left[\begin{array}{l} a \\ b \\ c \end{array}\right]=A^{-1} B=\frac{1}{18}\left(\begin{array}{ccc} 1 & -2 & 1 \\ -15 & 24 & -9 \\ 54 & -54 & 18 \end{array}\right)\left(\begin{array}{c} 64 \\ 133 \\ 208 \end{array}\right) \end{equation}\)
\(\begin{equation} =\frac{1}{18}\left(\begin{array}{c} 64-266+208 \\ -960+3192-1872 \\ 3456-7182+3744 \end{array}\right)=\frac{1}{18}\left(\begin{array}{c} 6 \\ 360 \\ 18 \end{array}\right)=\left(\begin{array}{c} 1 / 3 \\ 20 \\ 1 \end{array}\right) \end{equation}\)
Thus,\(\begin{equation} a=\frac{1}{3} \end{equation}\) ,b = 20 and c = 1
(i) (b)
(ii) (c)
(iii) (b) : \(\begin{equation} v(t)=\frac{1}{3} t^{2}+20 t+1 \end{equation}\)
(iv) (d) : Clearly, required speed = v(15)
\(\begin{equation} =\frac{1}{3} \times 225+20 \times 15+1 \end{equation}\)
= 75 + 300 + 1 = 376 miles per second
(v) (d) : Consider, v(t) = 784
\(\begin{equation} \Rightarrow \frac{1}{3} t^{2}+20 t+1=784 \end{equation}\)
\(\begin{equation} \Rightarrow \end{equation}\) t2 + 60t = 2349
\(\begin{equation} \Rightarrow \end{equation}\) t2+ (87 - 27)t - 2349 = 0
\(\begin{equation} \Rightarrow \end{equation}\) t(t + 87) - 27(t + 87) = 0
\(\begin{equation} \Rightarrow \end{equation}\) (t - 27)(t + 87) = 0
\(\begin{equation} \Rightarrow \end{equation}\) = 27 seconds [\(\therefore\) Time can't be negative] -
(i) (a) : Let \(\begin{equation} \Delta=\left|\begin{array}{cc} 1 & -2 \\ 4 & 3 \end{array}\right| \end{equation}\)
Cofactor of 1 = 3, cofactor of -2 =-4
Cofactor of 4 = 2, cofactor of 3 = 1
\(\therefore\) Required sum = 3 - 4 + 2 + 1 = 2
(ii) (b) : Let \(\begin{equation} \Delta=\left|\begin{array}{ccc} 5 & 6 & -3 \\ -4 & 3 & 2 \\ -4 & -7 & 3 \end{array}\right| \end{equation}\)
Minor of \(\begin{equation} a_{21}=\left|\begin{array}{cc} 6 & -3 \\ -7 & 3 \end{array}\right|=18-21=-3 \end{equation}\)
(iii) (c) : Let \(\begin{equation} \Delta=\left|\begin{array}{ccc} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{array}\right| \end{equation}\)
Clearly, a32 = 5
and A32 = cofactor of a32 in \(\begin{equation} \Delta=(-1)^{3+2}\left|\begin{array}{ll} 2 & 5 \\ 6 & 4 \end{array}\right| \end{equation}\)
= (-1)(8-30) = 22
\(\begin{equation} \therefore \end{equation}\) a32·A32 = 5 x 22 = 110
(iv) (d) : Here, \(\begin{equation} \Delta=\left|\begin{array}{lll} 5 & 3 & 8 \\ 2 & 0 & 1 \\ 1 & 2 & 3 \end{array}\right| \end{equation}\)
\(\therefore\) Minor of \(\begin{equation} a_{23}=\left|\begin{array}{ll} 5 & 3 \\ 1 & 2 \end{array}\right|=10-3=7 \end{equation}\)
(v) (b) : Here,\(\begin{equation} \Delta=\left|\begin{array}{ccc} 2 & -3 & 5 \\ 6 & 0 & 4 \\ 1 & 5 & -7 \end{array}\right| \end{equation}\)
\(\begin{equation} A_{11}=(-1)^{1+1}\left|\begin{array}{cc} 0 & 4 \\ 5 & -7 \end{array}\right|=1(0-20)=-20 \end{equation}\)
\(\begin{equation} A_{12}=(-1)^{1+2}\left|\begin{array}{cc} 6 & 4 \\ 1 & -7 \end{array}\right|=-1(-42-4)=46 \end{equation}\)
\(\begin{equation} A_{13}=(-1)^{1+3}\left|\begin{array}{ll} 6 & 0 \\ 1 & 5 \end{array}\right|=1(30-0)=30 \end{equation}\)
\(\begin{equation} \therefore \quad \Delta=a_{11} A_{11}+a_{12} a_{12}+a_{13} A_{13} \end{equation}\)
= 2(-20) -3(46) + 5(30) = -28
\(\begin{equation} \Rightarrow|\Delta|=28 \end{equation}\) -
(i) (c)
(ii) (b)
(iii) (b)
(iv) (b)
(v) (a) -
(i) (b) : x3 + x2y+ xy2+y3= 81
\(\begin{equation} \Rightarrow 3 x^{2}+x^{2} \frac{d y}{d x}+2 x y+2 x y \frac{d y}{d x}+y^{2}+3 y^{2} \frac{d y}{d x}=0 \end{equation}\)
\(\begin{equation} \Rightarrow \left(x^{2}+2 x y+3 y^{2}\right) \frac{d y}{d x}=-3 x^{2}-2 x y-y^{2} \end{equation}\)
\(\begin{equation} \Rightarrow \frac{d y}{d x}=\frac{-\left(3 x^{2}+2 x y+y^{2}\right)}{x^{2}+2 x y+3 y^{2}} \end{equation}\)
(ii) (c) : xy = ex-y⇒y log x = x - y
\(\begin{equation} \Rightarrow y \times \frac{1}{x}+\log x \cdot \frac{d y}{d x}=1-\frac{d y}{d x} \end{equation}\)
\(\begin{equation} \Rightarrow \frac{d y}{d x}[\log x+1]=1-\frac{y}{x} \Rightarrow \frac{d y}{d x}=\frac{x-y}{x[1+\log x]} \end{equation}\)
(iii) (d) : \(\begin{equation} e^{\sin y}=x y \Rightarrow \sin y=\log x+\log y \end{equation}\)
\(\begin{equation} \Rightarrow \cos y \frac{d y}{d x}=\frac{1}{x}+\frac{1}{y} \frac{d y}{d x} \Rightarrow \frac{d y}{d x}\left[\cos y-\frac{1}{y}\right]=\frac{1}{x} \end{equation}\)
\(\begin{equation} \Rightarrow \frac{d y}{d x}=\frac{y}{x(y \cos y-1)} \end{equation}\)
(iv) (d) : sin2x + cos2y = 1
\(\begin{equation} \Rightarrow \quad 2 \sin x \cos x+2 \cos y\left(-\sin y \frac{d y}{d x}\right)=0 \end{equation}\)
\(\begin{equation} \Rightarrow \frac{d y}{d x}=\frac{-\sin 2 x}{-\sin 2 y}=\frac{\sin 2 x}{\sin 2 y} \end{equation}\)
(v) (d) : \(\begin{equation} y=(\sqrt{x})^{\sqrt{x}} \quad \Rightarrow y=(\sqrt{x})^{y} \end{equation}\)
\(\begin{equation} \Rightarrow \log y=y(\log \sqrt{x}) \Rightarrow \log y=\frac{1}{2}(y \log x) \end{equation}\)
\(\begin{equation} \Rightarrow \frac{1}{y} \frac{d y}{d x}=\frac{1}{2}\left[y \times \frac{1}{x}+\log x\left(\frac{d y}{d x}\right)\right] \end{equation}\)
\(\begin{equation} \Rightarrow \frac{d y}{d x}\left\{\frac{1}{y}-\frac{1}{2} \log x\right\}=\frac{1}{2} \frac{y}{x} \end{equation}\)
\(\begin{equation} \Rightarrow \frac{d y}{d x}=\frac{y}{2 x} \times \frac{2 y}{(2-y \log x)}=\frac{y^{2}}{x(2-y \log x)} \end{equation}\) -
(i) (a) : Let x be the number of extra days after 1st July.
\(\therefore\) Price = Rs.(300 - 3Xx) = Rs.(300 - 3x)
Quantity = 80 quintals + x(1 quintal per day)
= (80 + x) quintals
(ii) (b) : R(x) = Quantity x Price
= (80 + x) (300 - 3x) = 24000 - 240x + 300x -3x2
= 24000 + 60x - 3x2
(iii) (a) : We have, R(x) = 24000 + 60x - 3x2
\(\begin{equation} \Rightarrow R^{\prime}(x)=60-6 x \Rightarrow R^{\prime \prime}(x)=-6 \end{equation}\)
For R(x) to be maximum, R'(x) = 0 and R"(x) < 0
\(\begin{equation} \Rightarrow 60-6 x=0 \Rightarrow x=10 \end{equation}\)
(iv) (a) : Shyams father will attain maximum revenue after 10 days.
So, he should harvest the onions after 10 days of 1st July i.e., on 11th July.
(v) (c) : Maximum revenue is collected by Shyams father when x = 10
\(\therefore\) Maximum revenue = R(10)
= 24000 + 60(10) - 3(10)2 = 24000 + 600 - 300 = 24300 -
(i) (c): When we solve an L.P.P. graphically, the optimal (or optimum) value of the objective function is attained at corner points of the feasible region.
(ii) (d): From the graph of 3x + 4y < 12 it is clear that it contains the origin but not the points on the line 3x + 4y = 12.
(iii) (d): Maximum of objective function occurs at corner points.Corner Points Value of Z = 2x + 5y (0,0) 0 (7,0) 14 (6,3) 27 (4,5) 33 ⇠ Maximum (0,6) 30 (iv) (d): Value of Z = px + qy at (15, 15) = 15p + 15q and that at (0, 20) = 20 q. According to given condition, we have
15p + 15q = 20q \(\Rightarrow\) 15p = 5q \(\Rightarrow\) q = 3p
(v) (b): Construct the following table of values of the objective function:Corner Points Value of Z = 4x + 3y (0,0) 4 × 0 + 3 × 0 = 0 (0,40) 4 x 0 + 3 x 40 = 120 (20,40) 4 x 20 + 3 x 40 = 200 (60,20) 4 x 60 + 3 x 20 = 300 ⇠ Maximum (60,0) 4 x 60 + 3 x 0 = 240 -
(i) (d) : Given, r cm is the radius and h cm is the height of required cylindrical can
Given that, volume = 3 l= 3000 cm3 \(\left(\because 1 l=1000 \mathrm{~cm}^{3}\right)\)
\(\Rightarrow \pi r^{2} h=3000 \Rightarrow h=\frac{3000}{\pi r^{2}}\)
Now, the surface area, as a function of r is given by
\(S(r)=2 \pi r^{2}+2 \pi r h=2 \pi r^{2}+2 \pi r\left(\frac{3000}{\pi r^{2}}\right)\)
\(=2 \pi r^{2}+\frac{6000}{r}\)
(ii) (c) : Now, \(S(r)=2 \pi r^{2}+\frac{6000}{r}\)
\(\Rightarrow S^{\prime}(r)=4 \pi r-\frac{6000}{r^{2}}\)
To find criti£al points, put S'(r) = 0
\(\Rightarrow \frac{4 \pi r^{3}-6000}{r^{2}}=0\)
\(\Rightarrow r^{3}=\frac{6000}{4 \pi} \Rightarrow r=\left(\frac{1500}{\pi}\right)^{1 / 3}\)
Also, \(\left.S^{\prime \prime}(r)\right|_{r=} \sqrt[3]{\frac{1500}{\pi}}=4 \pi+\frac{12000 \times \pi}{1500}\)
\(=4 \pi+8 \pi=12 \pi>0\)
Thus, the critical point is the point of minima.
(iii) (b) : The cost of material for the tin can is minimized when \(r=\sqrt[3]{\frac{1500}{\pi}} \mathrm{cm}\) and the height is \(\frac{3000}{\pi\left(\sqrt[3]{\frac{1500}{\pi}}\right)^{2}}=2 \sqrt[3]{\frac{1500}{\pi}} \mathrm{cm} .\) .
(iv) (a) : We have,minimum surface area = \(\frac{2 \pi r^{3}+6000}{r}\) .
\(=\frac{2 \pi \cdot \frac{1500}{\pi}+6000}{\sqrt[3]{\frac{1500}{\pi}}}=\frac{9000}{7.8}=1153.84 \mathrm{~cm}^{2}\)
Cost of 1 m2 material = Rs.100
\(\therefore \ \text { Cost of } 1 \mathrm{~cm}^{2} \text { material }=Rs. \frac{1}{100}\)
\(\therefore \ \text { Minimum cost }=Rs. \frac{1153.84}{100}=Rs. 11.538\)
(v) (c) : To minimize the cost we need to minimize the total surface area. -
(i) (c)
(ii) (b): Since (8, 12) satisfy all the inequalities therefore (8, .1.2) is the point in its feasible region.
(iii) (c) : At (0, 0), z = 0
At (16, 0), z = 352
At (8, 12), z = 392
At (0, 20), z = 360
It can be observed that max z occur at (8, 12). Thus, z will attain its optimal value at (8, 12).
(iv) (c) : We have, x + y = 20 ... (i)
and 3x + 2y = 48.. (ii)
On solving (i) and (ii), we get
X = 8, y = 12.
Thus, the coordinates of P are (8,12) and hence (8, 12) is one of its corner points.
(v) (b): The optimal solution occurs at every point on the line joining these two points. -
(i) (d) : In order to make least expensive water tank, Nitin need to minimize its cost.
(ii) (d) : Let 1ft be the length and h ft be the height of the tank. Since breadth is equal to 5 ft. (Given)
\(\therefore\) Two sides will be 5h sq. feet and two sides will be
1h sq. feet. So, the total area of the sides is (10 h + 2 1h)ft2
Cost of the sides is Rs.10 per sq. foot. So, the cost to build the sides is (10h + 21h) x 10 = Rs.(100h + 20lh)
Also, cost of base = (5l) x 20 = Rs. 100 l
\(\therefore\) Total cost of the tank in Rs. is given by
c = 100 h + 20 I h + 100 l
Since, volume of tank = 80ft3
\(\therefore \quad 5 l h=80 \mathrm{ft}^{3} \quad \therefore l=\frac{80}{5 h}=\frac{16}{h}\)
\(\therefore \quad c(h)=100 h+20\left(\frac{16}{h}\right) h+100\left(\frac{16}{h}\right)\)
\(=100 h+320+\frac{1600}{h}\)
(iii) (b) : Since, all side lengths must be positive
\(\therefore \quad h>0\) and \(\frac{16}{h}>0\)
Since, \(\frac{16}{h}>0, \text { whenever } h>0\)
\(\therefore \text { Range of } h \text { is }(0, \infty)\)
(iv) (a) : To minimize cost, \(\frac{d c}{d h}=0\)
\(\Rightarrow \quad 100-\frac{1600}{h^{2}}=0\)
\(\Rightarrow 100 h^{2}=1600 \Rightarrow h^{2}=16 \Rightarrow h=\pm 4\)
\(\Rightarrow h=4\) [\(\therefore\) height can not be negative]
(v) (c) : Cost of least expensive tank is given by
\(c(4)=400+320+\frac{1600}{4}\)
= 720 + 400 = Rs. 1120 -
Let E be the event that the doctor visit the patient late and let A1, A2, A3, A4 be the events that the doctor comes by cab, metro, bike and other means of transport respectively.
\(P\left(A_{1}\right)=0.3, P\left(A_{2}\right)=0.2, P\left(A_{3}\right)=0.1, P\left(A_{4}\right)=0.4\)
P(E I A1) = Probability that the doctor arriving late when he comes by cab = 0.25
Similarly, P ( E I A2) = 0.3, P (E I A3) = 0.35 and P ( E I A3) = 0.1
(i) (b): P(A2 | E) = Probability that the doctor arriving late and he comes by metro
\(=\frac{P\left(A_{2}\right) P\left(E \mid A_{2}\right)}{\sum P\left(A_{i}\right) P\left(E \mid A_{i}\right)}\)
\(=\frac{(0.2)(0.3)}{(0.3)(0.25)+(0.2)(0.3)+(0.1)(0.35)+(0.4)(0.1)}\)
\(=\frac{0.06}{0.21}=\frac{2}{7}\)
(ii) (c): P(A1 | E) = Probability that the doctor arriving late and he comes by cab
\(=\frac{P\left(A_{1}\right) P\left(E \mid A_{1}\right)}{\Sigma P\left(A_{i}\right) P\left(E \mid A_{i}\right)}\)
\(=\frac{(0.3)(0,25)}{(0.3)(0.25)+(0.2)(0.3)+(0.1)(0.35)+(0.4)(0.1)}\)
\(=\frac{0.075}{0.21}=\frac{5}{14}\)
(iii) (d): P(A3| E) = Probability that the doctor arriving late and he comes by bike
\(=\frac{P\left(A_{3}\right) P\left(E \mid A_{3}\right)}{\sum P\left(A_{i}\right) P\left(E \mid A_{i}\right)}\)
\(=\frac{(0.1)(0.35)}{(0.3)(0.25)+(0.2)(0.3)+(0.1)(0.35)+(0.4)(0.1)}\)
\(=\frac{0.035}{0.21}=\frac{1}{6}\)
(iv) (c): P(A4 | E) = Probability that the doctor arriving late and he comes by other means of transport
\(=\frac{P\left(A_{4}\right) P\left(E \mid A_{4}\right)}{\Sigma P\left(A_{i}\right) P\left(E \mid A_{i}\right)}\)
\(=\frac{(0.4)(0.1)}{(0.3)(0.25)+(0.2)(0.3)+(0.1)(0.35)+(0.4)(0.1)}\)
\(=\frac{0.04}{0.21}=\frac{4}{21}\)
(v) (a): Probability that the doctor is late by any means
\(=\frac{2}{7}+\frac{5}{14}+\frac{1}{6}+\frac{4}{21}=1\) -
(i) (b): Required probability = \(\frac{{ }^{12} C_{2}}{{ }^{51} C_{2}}\)
\(=\frac{12 \times 11}{51 \times 50}=\frac{22}{425}\)
(ii) (a): Required probability = \(\frac{{ }^{13} C_{2}}{{ }^{51} C_{2}}=\frac{13 \times 12}{51 \times 50}=\frac{26}{425}\)
(iii) (b): Clearly, P(A l E1) = \(\frac{{ }^{12} C_{2}}{{ }^{51} C_{2}}=\frac{22}{425}\)
\(P\left(A \mid E_{2}\right)=\frac{{ }^{13} C_{2}}{{ }^{51} C_{2}}=\frac{26}{425} \)
\(P\left(A \mid E_{3}\right)=P\left(A \mid E_{4}\right)=\frac{26}{425}\)
\(\therefore \sum_{i=1}^{4} P\left(A \mid E_{i}\right)=\frac{22}{425}+\frac{26}{425}+\frac{26}{425}+\frac{26}{425}=\frac{100}{425}=0.24\)
(iv) (b): P(getting both king) = \(\frac{{ }^{4} C_{2}}{{ }^{52} C_{2}}=\frac{4 \times 3}{52 \times 51}=\frac{1}{221}\)
(v) (a): P(drawing a king) = \(\frac{4}{52}=\frac{1}{13}\)
\( \therefore \quad P(\text { not drawing a king })=1-\frac{1}{13}=\frac{12}{13} \)
\(\therefore \quad \text { Required probability }=\frac{12}{13} \times \frac{12}{13}=\frac{144}{169}\) -
(i) (b): Total number of tickets = 50
Let event A = First ticket shows even number and B = Second ticket shows even number
Now, P(Both tickets show even number) = P(A)・P(B | A)
\(=\frac{25}{50} \cdot \frac{24}{49}=\frac{12}{49}\)
(ii) (c): Let the event A = First ticket shows odd number and B = Second ticket shows odd number
P (Both tickets show odd number)
\(=\frac{25}{50} \times \frac{24}{49}=\frac{12}{49}\)
(iii) (c): Required probability = P(one number is a multiple of 4 and other is a multiple of 5)
= P(multiple of 5 on first ticket and multiple of 4 on second ticket) + P(multiple of 4 on first ticket and multiple of 5 on second ticket)
\(=\frac{10}{50} \cdot \frac{12}{49}+\frac{12}{50} \times \frac{10}{49}=\frac{12}{245}+\frac{12}{245}=\frac{24}{245}\)
(iv) (d): Required probability = P(one ticket with prime number and other ticket with a multiple of 4)
\(=2\left(\frac{15}{50} \times \frac{12}{49}\right)=\frac{36}{245}\)
(v) (b): Let the event A = First ticket shows even number and B = Second ticket shows odd number.
Now, P(First ticket shows an even number and second ticket shows an odd number) = P(A)・P(B | A)
\(=\frac{25}{50} \times \frac{25}{49}=\frac{25}{98}\) -
(i) (d) : If x be the amount of increase in annual charges, then number of subscriber reduces to 5000 - x.
\(\therefore\) Revenue, R(x) = (3000 + x) (5000 - x)
\(=15000000+2000 x-x^{2}, 0
(ii) (a) : Clearly, at x = 500
R(500) = 15000000 + 2000(500) - (500)2
= 15000000 + 1000000 - 250000 = Rs.15750000
(iii) (c) : Since, 15000000 + 2000x - x2 = 15640000 (Given)
\(\Rightarrow x^{2}-2000 x+640000=0\)
\(\Rightarrow \quad x^{2}-1600 x-400 x+640000=0\)
\(\Rightarrow x(x-1600)-400(x-1600)=0 \Rightarrow x=400,1600\)
(iv) (a) : \(\frac{d R}{d x}=2000-2 x\) and \(\frac{d^{2} R}{d x^{2}}=-2<0\)
For maximum revenue, \(\frac{d R}{d x}=0 \Rightarrow x=1000\)
\(\therefore\) Required amount = Rs. 1000
(v) (b) : Maximum revenue = R(1000)
= (3000 + 1000) (5000 - 1000)
= 4000 x 4000 = ~ 16000000
Case Study Questions






































