CBSE 12th Standard Physics Subject Case Study Questions With Solution 2021 Part - I
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 12 , and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Case Study Questions With Solution 2021 Part - I
12th Standard CBSE
-
Reg.No. :
Physics
-
Coulomb's law states that the electrostatic force of attraction or repulsion acting between two stationary point charges is given by
\(F=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)

where F denotes the force between two charges q1 and q2 separated by a distance r in free space, Eo is a constant known as permittivity of free space. Free space is vacuum and may be taken to be air practically.
If free space is replaced by a medium, then Eo is replaced by (Eok) or (EoEr)where k is known as dielectric constant or relative permittivity.
(i) In coulomb's law, F = \(k \frac{q_{1} q_{2}}{r^{2}}\), then on which of the following factors does the proportionality constant k depends?(a) Electrostatic force acting between the two charges (b) Nature of the medium between the two charges (c) Magnitude of the two charges (d) Distance between the two charges (ii) Dimensional formula for the permittivity constant Eo of free space is
\(\text { (a) }\left[\mathrm{ML}^{-3} \mathrm{~T}^{4} \mathrm{~A}^{2}\right]\) \(\text { (b) }\left[M^{-1} L^{3} T^{2} A^{2}\right]\) \(\text { (c) }\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{~A}^{2}\right]\) \(\text { (d) }\left[M L^{-3} T^{4} A^{-2}\right]\) (iii) The force of repulsion between two charges of 1 C each, kept 1 m apart in vaccum is
\(\text { (a) } \frac{1}{9 \times 10^{9}} \mathrm{~N}\) \(\text { (b) }\left[M^{-1} L^{3} T^{2} A^{2}\right]\) \(\text { (c) } 9 \times 10^{7} \mathrm{~N}\) \(\text { (d) } \frac{1}{9 \times 10^{12}} \mathrm{~N}\) (iv) Two identical charges repel each other with a force equal to 10 mgwt when they are 0.6 m apart in air. (g = 10 ms-2). The value of each charge is
(a) 2 mC (b) 2 x10-7 mC (c) 2 nC (d) 2\(\mu \)C (v) Coulomb's law for the force between electric charges most closely resembles with
(a) law of conservation of energy (b) Newton's law of gravitation (c) Newton's 2nd law of motion (d) law of conservation of charge (a) -
The potential at any observation point P of a static electric field is defined as the work done by the external agent (or negative of work done by electrostatic field) in slowly bringing a unit positive point charge from infinity to the observation point. Figure shows the potential variation along the line of charges. Two point charges Q1 and Q2 lie along a line at a distance from each other.
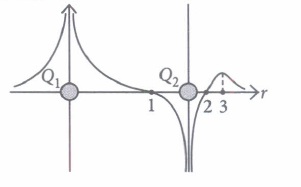
(i) At which of the points 1, 2 and 3 is the electric field is zero?(a) 1 (b) 2 (c) 3 (d) Both (a) and (b) (ii) The signs of charges Q1 and Q2 respectively are
(a) positive and negative (b) negative and positive (c) positive and positive (d) negative and negative
(iii) Which of the two charges Q1 and Q2 is greater in magnitude?(a) Q2 (b) Q1 (c) Same (d) Can't determined (iv) Which of the following statement is not true?
(a) Electrostatic force is a conservative force (b) Potential energy of charge q at a point is the work done per unit charge in bringing a charge from any point to infinity (c) When two like charges lie infinite distance apart, their potential energy is zero. (d) Both (a) and (c). (v) Positive and negative point charges of equal magnitude are kept at \(\left(0,0, \frac{a}{2}\right)\) and \(\left(0,0, \frac{-a}{2}\right)\) respectively.
The work done by the electric field when another positive point charge is moved from (-a, 0, 0) to (0, a, 0) is(a) positive (b) negative (c) zero (d) depends on the path connecting the initial and final positions (a) -
Emf of a cell is the maximum potential difference between two electrodes of the cell when no current is drawn from the cell. Internal resistance is the resistance offered by the electrolyte of a cell when the electric current flows through it. The internal resistance of a cell depends upon the following factors;
(i) distance between the electrodes
(ii) nature and temperature of the electrolyte
(iii) nature of electrodes
(iv) area of electrodes.
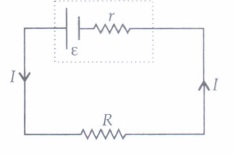
For a freshly prepared cell, the value of internal resistance is generally low and goes on increasing as the cell is put to more and more use. The potential difference between the two electrodes of a cell in a closed circuit is called terminal potential difference and its value is always less than the emf of the cell in a closed circuit. It can be written as V = E - Jr.
(i) The terminal potential difference of two electrodes of a cell is equal to emf of the cell when\(\text { (a) } I \neq 0\) (b) I=0 (c) both (a) and (b) (d) neither (a)nor (b) (ii) A cell of emf E and internal resistance r gives a current of 0.5 A with an external resistance of \(12 \Omega\) and a current of 0.25 A with an external resistance of \(25 \Omega\) .What is the value of internal resistance of the cell?
\(\text { (a) } 5 \Omega\) \(\text { (b) } 1 \Omega\) \(\text { (c) } 7 \Omega\) \(\text { (d) } 3 \Omega\) (iii) Choose the wrong statement.
(a) Potential difference across the terminals of a cell in a closed circuit is always less than its emf. (b) Internal resistance of a cell decrease with the decrease in temperature of the electrolyte. (c) Potential difference versus current graph for a cell is a straight line with a -ve slope (d) Terminal potential difference of the cell when it is being charged is given as V = E + Ir. (iv) An external resistance R is connected to a cell of internal resistance r, the maximum current flows in the external resistance, when
(a) R = r (b) R < r (c) R> r (d) R=l/r (v) IF external resistance connected to a cell has been increased to 5 times, the potential difference across the terminals of the cell increases from 10 V to 30 V. Then, the emf of the cell is
(a) 30 V (b) 60V (c) 50 V (d) 40 V (a) -
The path of a charged particle in magnetic field depends upon angle between velocity and magnetic field.If velocity \(\vec{v}\) is at angle \(\theta\) to \(\vec{B}\) component of velocity parallel to magnetic field \((v \cos \theta)\) remains constant and component of velocity perpendicular to magnetic field \((v \sin \theta)\) is responsible for circular motion, thus the charge particle moves in a helical path.
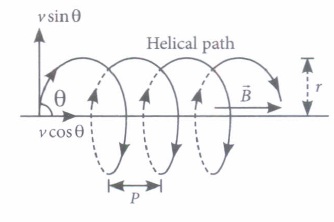
The plane of the circle is perpendicular to the magnetic field and the axis of the helix is parallel to the magnetic field. The charged particle. moves along helical path touching the line parallel to the magnetic field passing through the starting point after each rotation.
Radius of circular path is \(r=\frac{m v \sin \theta}{1 v_{q} B}\)
Hence the resultant path of the charged particle will be a helix, with its axis along the direction of \(\vec{B}\) as shown in figure.
(i) When a positively charged particle enters into a uniform magnetic field with uniform velocity, its trajectory can be (i) a straight line (ii) a circle (iii) a helix.(a) (i) only (b) (i) or (ii) (c) (i) or (iii) (d) anyone of (i), (ii) and (iii) (ii) Two charged particles A and B having the same charge, mass and speed enter into a magnetic field in such a way that the initial path of A makes an angle of 30° and that of B makes an angle of 90° with the field. Then the trajectory of
(a) B will have smaller radius of curvature than that of A (b) both will have the same curvature (c) A will have smaller radius of curvature than that of B (d) both will move along the direction of their original velocities. (iii) An electron having momentum 2.4 x 10-23kg m/ s enters a region of uniform magnetic field of 0.15 T. The field vector makes an angle of 30° with the initial velocity vector of the electron. The radius of the helical path of the electron in the field shall be
(a) 2 mm (b) 1 mm \(\text { (c) } \frac{\sqrt{3}}{2} \mathrm{~mm}\) (d) 0.5 mm (iv) The magnetic field in a certain region of space is given by \(\vec{B}=8.35 \times 10^{-2} \hat{i}\) T. A proton is shot into the field with velocity \(\vec{v}=\left(2 \times 10^{5} \hat{i}+4 \times 10^{5} \hat{j}\right) \mathrm{m} / \mathrm{s}\) The proton follows a helical path in the field. The distance moved by proton in the x-direction during the period of one revolution in the yz-plane will be
(Mass of proton = 1.67 x 10-27kg)(a) 0.053 m (b) 0.136 m (c) 0.157 m (d) 0.236 m (v) The frequency of revolution of the particle is
\(\text { (a) } \frac{m}{q B}\) \(\text { (b) } \cdot \frac{q B}{2 \pi m}\) \(\text { (c) } \frac{2 \pi R}{v \cos \theta}\) \(\text { (d) } \frac{2 \pi R}{v \sin \theta}\) (a) -
By analogy to Gauss's law of electrostatics, we can write Gauss's law of magnetism as \(\oint \vec{B} \cdot d \vec{s}=\mu_{0} m_{\text {inside }}\) where \(\oint \vec{B} \cdot d \vec{s}\) is the magnetic flux and \(m_{\text {inside }}\) is the net pole strength inside the closed surface.
We do not have an isolated magnetic pole in nature. At least none has been found to exist till date. The smallest unit of the source of magnetic field is a magnetic dipole where the net magnetic pole is zero. Hence, the net magnetic pole enclosed by any closed surface is always zero. Correspondingly, the flux of the magnetic field through any closed surface is zero.
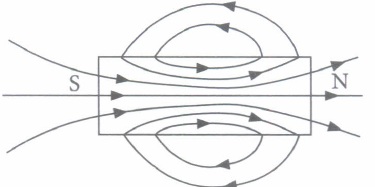
(I) Consider the two idealised systems
(i) a parallel plate capacitor with large plates and small separation and
(ii) a long solenoid oflength L >> R, radius of cross-section.
In (i) \(\vec{E}\) is ideally treated as a constant between plates and zero outside. In (ii) magnetic field is constant inside the solenoid and zerq outside. These idealised assumptions, however, contradict fundamental laws as below(a) case (i) contradicts Gauss's law for electrostatic fields (b)case (ii) contradicts Gauss's aw for magnetic fields \(\text { (c) case (i) agrees with } \oint \vec{E} \cdot \overrightarrow{d l}=0 \text { . }\) \(\text { (d) case (ii) contradicts } \oint \vec{H} \cdot \overrightarrow{d l}=I_{e n}\) (ii) The net magnetic flux through any closed surface, kept in a magnetic field is
(a) zero \(\text { (b) } \frac{\mu_{0}}{4 \pi}\) \(\text { (c) } 4 \pi \mu_{0}\) \(\text { (d) } \frac{4 \mu_{0}}{\pi}\) (iii) A closed surface S encloses a magnetic dipole of magnetic moment 2ml. The magnetic flux emerging from the surface is
\(\text { (a) } \mu_{0} m\) (b) zero \(\text { (c) } 2 \mu_{0} m\) \(\text { (d) } \frac{2 m}{\mu_{0}}\) (iv) Which of the following is not a consequence of Gauss's law?
(a) The magnetic poles always exist as unlike pairs of equal strength. (b) If several magnetic lines of force enter in a closed surface, then an equal number of lines of force must leave that surface (c) There are abundant sources or sinks of the magnetic field inside a closed surface (d) Isolated magnetic poles do not exist (v) The surface integral of a magnetic field over a surface
(a) is proportional to mass enclosed (b) is proportional to charge enclosed (c) is zero (d) equal to its magnetic flux through that surface. (a) -
Mutual inductance is the phenomenon of inducing emf in a coil, due to a change of current in the neighbouring coil. The amount of mutual inductance that links one coil to another depends very much on the relative positioning of the two coils, their geometry and relative separation between them. Mutual inductance between the two coils increases \(\mu_{r}\) times if the coils are wound over an iron core of relative permeability \(\mu_{r}\).
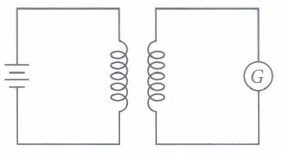
(I) A short solenoid of radius a, number of turns per unit length nI' and length L is kept coaxially inside a very long solenoid of radius b, numbdr of turns per unit length n2• What is the mutual inductance of the system?\(\text { (a) } \mu_{0} \pi b^{2} n_{1} n_{2} L\) \(\text { (b) } \mu_{0} \pi a^{2} n_{1} n_{2} L^{2}\) \(\text { (c) } \mu_{0} \pi a^{2} n_{1} n_{2} L\) \(\text { (d) } \mu_{0} \pi b^{2} n_{1} n_{2} L^{2}\) (ii) If a change in current of 0.01 A in one coil produces a change in magnetic flux of 2 x l0-2 weber in another coil, then the mutual inductance between coils is
(a) 0 (b) 0.5 H (c) 2 H (d) 3 H (iii) Mutual inductance of two coils can be increased by
(a) decreasing the number of turns in the coils (b) increasing the number of turns in the coils (c) winding the coils on wooden cores (d) none of these (iv) When a sheet of iron is placed in between the two co-axial coils, then the mutual inductance between the coils will
(a) increase (b) decrease (c) remains same (d) cannot be predicted (v) The SI unit of mutual inductance is
(a) ohm (b) mho (c) henry (d) none of these (a) -
The power averaged over one full cycle of a.c. is known as average power. It is also known as true power
\(P_{\mathrm{av}}=V_{\mathrm{rms}} I_{\mathrm{rms}} \cos \phi=\frac{V_{0} I_{0}}{2} \cos \phi\)
Root mean square or simply rms watts refer to continuous power
A circuit containing a 80.mH inductor and a \(60 \mu \mathrm{F}\) capacitor in series is connected to a 230 V, 50 Hz supply. The resistance of the circuit is negligible.
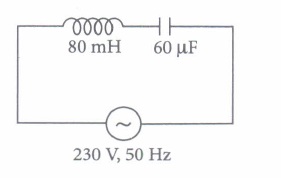
(i) The value of current amplitude is(a) 15 A (b) 11.63 A (c) 17.65 A (d) 6.33 A (ii) Find rms value.
(a) 6 A (b) 5.25 A (c) 8.23 A (d) 7.52A (iii) The average power transferred to inductor is
(a) zero (b) 7W (c) 2.5 W (d) 5 W (iv) The average power transferred to the capacitor is
(a) 5 W (b) zero (c) 11 W (d) 15 W (v) What is the total average power absorbed by the circuit?
(a) zero (b) 10W (c) 2.5 W (d) 15W (a) -
A stationary charge produces only an electrostatic field while a charge in uniform motion produces a magnetic field, that does not change with time. An oscillating charge is an example of accelerating charge. It produces an oscillating magnetic field, which in turruproduces an oscillating electric fields and so on. The oscillating electric and magnetic fields regenerate each other as a wave which propagates through space.
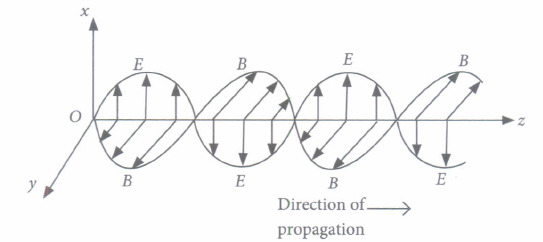
(i) Magnetic field in a plane electromagnetic wave is given by \(\vec{B}=B_{0} \sin (k x+\omega t) \hat{j} \mathrm{~T}\) Expression for corresponding electric field will be (Where C is speed of light.)\((a) \vec{E}=-B_{0} c \sin (k x+\omega t) \hat{k} \mathrm{~V} / \mathrm{m}\) \((b) \vec{E}=B_{0} c \sin (k x-\omega t) \hat{k} \mathrm{~V} / \mathrm{m}\) \((c) \vec{E}=\frac{B_{0}}{c} \sin (k x+\omega t) \hat{k} \mathrm{~V} / \mathrm{m}\) \((d) \vec{E}=B_{0} c \sin (k x+\omega t) \hat{k} \mathrm{~V} / \mathrm{m}\) (ii) The electric field component of a monochromatic radiation is given by \(\vec{E}=2 E_{0} \hat{i} \cos k z \cos \omega t\) .Its magnetic field \(\vec{B}\) is then given by
\((a) \frac{2 E_{0}}{c} \hat{j} \cos k z \cos \omega t\) \((b) \frac{2 E_{0}}{c} \hat{j} \sin k z \cos \omega t\) \((c) \frac{2 E_{0}}{c} \hat{j} \sin k z \sin \omega t\) \((d) -\frac{2 E_{0}}{c} \hat{j} \sin k z \sin \omega t\) (iii) A plane em wave of frequency 25 MHz travels in a free space along x-direction. At a particular point in space and time, \(E=(6.3 \hat{j}) \mathrm{V} / \mathrm{m}\) What is magnetic field at that time?
\((a) 0.095 \mu \mathrm{T}\) \((b) 0.124 \mu \mathrm{T}\) \((c) 0.089 \mu \mathrm{T}\) \((d) 0.021 \mu \mathrm{T}\) (iv) A plane electromagnetic wave travelling along the x-direction has a wavelength of 3 mm. The variation in the electric field occurs in the y-direction with an amplitude 66 V m-1. The equations for the electric and magnetic fields as a function of x and t are respectively
\((a) E_{y}=33 \cos \pi \times 10^{11}\left(t-\frac{x}{c}\right), B_{z}=1.1 \times 10^{-7} \cos \pi \times 10^{11}\left(t-\frac{x}{c}\right)\) \((b) E_{y}=11 \cos 2 \pi \times 10^{11}\left(t-\frac{x}{c}\right), \quad B_{y}=11 \times 10^{-7} \cos 2 \pi \times 10^{11}\left(t-\frac{x}{c}\right)\) \((c) E_{x}=33 \cos \pi \times 10^{11}\left(t-\frac{x}{c}\right), \quad B_{x}=11 \times 10^{-7} \cos \pi \times 10^{11}\left(t-\frac{x}{c}\right)\) \((d) E_{y}=66 \cos 2 \pi \times 10^{11}\left(t-\frac{x}{c}\right), \quad B_{z}=2.2 \times 10^{-7} \cos 2 \pi \times 10^{11}\left(t-\frac{x}{c}\right)\) (v) A plane electromagnetic wave travels in free space along x-axis. At a particular point in space, the electric field along y-axis is 9.3 V m-1. The magnetic induction (B) along z-axis is
(a) 3.1 x 10-8 T (b) 3 x 10-5 T (c) 3 x 10-6 T (d) 9.3 x 10-6 T (a) -
A compound microscope is an optical instrument used for observing highly magnified images of tiny objects. Magnifying power of a compound microscope is defined as the ratio of the angle subtended at the eye by the final image to the angle subtended at the eye by the object, when both the final image and the object are situated at the least distance of distinct vision from the eye. It can be given that:\(m=m_{e} \times m_{o}\) where me is magnification
produced by eye lens and mo is magnification produced by objective lens. Consider a compound microscope that consists of an objective lens of focal length 2.0 cm and an eyepiece of focal length 6.25 cm separated by a distance of 15 cm.
(i) The object distance for eye-piece, so that final image is formed at the least distance of distinct vision, will be(a) 3.45 cm (b) 5.cm (c) 1.29 cm (d) 2.59 cm (ii) How far from the objective should an object be placed in order to obtain the condition described in part(i)?
(a) 4.5 cm (b) 2.5 cm (c) 1.5 cm (d) 3.0 cm (iii) What is the magnifying power of the microscope in case ofleast distinct vision?
(a) 20 (b) 30 (c) 40 (d) 10 (iv) The intermediate image formed by the objective of a compound microscope is
(a) real, inverted and magnified (b) real, erect, and magnified (c) virtual, erect and magnified (d) virtual, inverted and magnified (v) The magnifying power of a compound microscope increases with
(a) the focal length of objective lens is increased and that of eye lens is decreased (b) the focal length of eye lens is increased and that of objective lens is decreased (c) focal lengths of both objects and eye-piece are increased (d) focal lengths of both objects and eye-piece are decreased. (a) -
When light from a monochromatic source is incident on a single narrow slit, it gets diffracted and a pattern of alternate bright and dark fringes is obtained on screen, called "Diffraction Pattern" of single slit. In diffraction pattern of single slit, it is found that
(I) Central bright fringe is ·of maximum intensity and the intensity of any secondary bright fringe decreases with increase in its order.
(II) Central bright fringe is twice as wide as any other secondary bright or dark fringe .
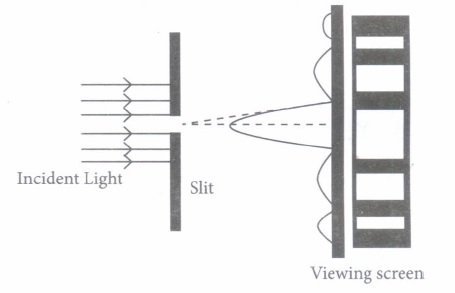
(i) A single slit of width 0.1 mm is illuminated by a parallel beam of light of wavelength 6000 A and diffraction bands are observed on a screen 0.5 m from the slit. The distance of the third dark band from the central bright band is(a) 3 mm (b) 1.5 mm (c) 9 mm (d) 4.5 mm (ii) In Fraunhofer diffraction pattern, slit width is 0.2 mm and screen is at 2 m away from the lens. If wavelength of light used is 5000 \(\lambda\) then the distance between the first minimum on either side the central maximum is
(a) 10-1 m (b) 10-2 m (c) 2 x 10-2 m (d) 2 x 10-1 m (iii) Light of wavelength 600 nm is incident normally on a slit of width 0.2 mm. The angular width of central maxima in the diffraction pattern is (measured from minimum to minimum)
(a) 6 x 10-3 rad (b) 4 x 10-3 rad (c) 2.4 x 10-3 rad (d) 4.5 x 10-3 rad (iv) A diffraction pattern is obtained by using a beam of red light. What will happen, if the red light is replaced by the blue light?
(a) bands disappear (b) bands become broader and farther apart (c) no change will take place (d) diffraction bands become narrower and crowded together. (v) To observe diffraction, the size of the obstacle
(a) should be A/2, where A is the wavelength. (b) should be of the order of wavelength. (c) has no relation to wavelength. (d) should be much larger than the wavelength. (a) -
If we allow radiations of a fixed frequency to fall on plate and the accelerating potential difference between the two electrodes is kept fixed, then the photoelectric current is found to increase linearly with the intensity of incident radiation. Here, radiation pressure is P = \(\left(\frac{1+e}{C}\right) I\). As, atmosphere pressure at sea level is 105Pa. If the intensity of light of a given wavelength, is increased, there is an increase in the number of photons incident on a given area in a given time. But the energy of each photon remain the same.
(i) The number of photons hitting the cone second\(\text { (a) } \pi R^{2} I / 2 E\) \(\text { (b) } 2 \pi R^{2} I / E\) \(\text { (c) } \pi R^{2} I / 4 E\) \(\text { (d) } \pi R^{2} I / E\) (ii) A radiation of energy E falls normally on a perfect reflecting surface. The momentum transferred to the surface is
\(\text { (a) } \frac{E}{c}\) \(\text { (b) } \frac{2 E}{c}\) \(\text { (c) } E c\) \(\text { (d) } \frac{E}{c^{2}}\) (iii) Which one is correct?
\(\text { (a) } E^{2}=p^{2} c^{2}\) \(\text { (b) } E^{2}=p^{2} c\) \(\text { (c) } E^{2}=p^{2}\) \(\text { (d) } E^{2}=\frac{p^{2}}{c^{2}}\) (iv) The incident intensity on a horizontal surface at sea level from the Sun is about 1 k W m-2. Assuming that 50% of this intensity is reflected and 50% is absorbed, determine the radiation pressure on this horizontal surface.
(a) 8.2 x 10-2 Pa (b) 5 x 10-6 Pa (c) 3 x 10-5 Pa (d) 6 x 10-5 Pa (v) Find the ratio of radiation pressure to atmospheric pressure P0 about 1 x 105 Pa at sea level.
(a) 5 x 10-11 (b) 4 x 10-8 (c) 6 x 10-12 (d) 8 x 10-11 (a) -
Hydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr, this electron moves in a stationary orbit. When this electron & I is in the stationary orbit, it emits no electromagnetic radiation. The angular momentum of the electron is quantized, i.e., mvr = \((n h / 2 \pi)\) where m = mass of the electron, v = velocity of the electron in the orbit, r = radius of the orbit and n = 1,2, 3, .... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is \(\lambda\)y we find that \(\frac{1}{\lambda}=R\left[\frac{1}{J^{2}}-\frac{1}{K^{2}}\right]\) where R is Rydberg's constant.
On a different planet, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P = 2n(h/2\(\pi\) ), i.e., an even multiple of (h/2\(\pi\)).
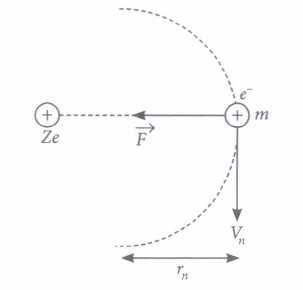
(i) The minimum permissible radius of the orbit will be\(\text { (a) } \frac{2 \varepsilon_{0} h^{2}}{m \pi e^{2}}\) \(\text { (b) } \frac{4 \varepsilon_{0} h^{2}}{m \pi e^{2}}\) \(\text { (c) } \frac{\varepsilon_{0} h^{2}}{m \pi e^{2}}\) \(\text { (d) } \frac{\varepsilon_{0} h^{2}}{2 m \pi e^{2}}\) (ii) In our world, the velocity of electron is V0 when the hydrogen atom is in the ground state. The velocity of electron in this state on the other .planet should be
(a) V0 (b) V0/2 (c) V0/4 (d) V0/8 (iii) In our world, the ionization potential energy of a hydrogen atom is 13.6 ev On the other planet, this ionization potential energy will be
(a) 13.6 eV (b) 3.4 eV (c) 1.5 eV (d) 0.85 eV (iv) Check the correctness of the following statements about the Bohr model of hydrogen atom
(i) The acceleration of the electron in n = 2 orbit is more than that in n = 1 orbit.
(ii) The angular momentum of the electron in n = 2 orbit is more than that in n = 1 orbit.
(iii) The kinetic energy of the electron in n = 2 orbit is less than that in n = 1 orbit.(a) Only (iii) and (i) are correct. (b) Only (i) and (ii) are correct. (c) Only (ii) and (iii) are correct. (d) All the statements are correct (v) In Bohr's model of hydrogen atom, let PE represent potential energy and TE the total energy. In going to a higher orbit
(a) PE increases, TE decreases (b) PE decreases, TE increases (c) PE increases, TE increases (d) PE decreases, TE decreases (a) -
The density of nuclear matter is the ratio of the mass of a nucleus to its volume. As the volume of a nucleus is directly proportional to its mass number A, so the density of nuclear matter is independent of the size of the nucleus. Thus, the nuclear matter behaves like a liquid of constant density. Different nuclei are like drops of this liquid, of different sizes but of same density.
Let A be the mass number and R be the radius of a nucleus. If m is the average mass of a nucleon, then
Mass of nucleus = mA
\(\text { Volume of nucleus }=\frac{4}{3} \pi R^{3}=\frac{4}{3} \pi\left(R_{0} A^{1 / 3}\right)^{3}=\frac{4}{3} \pi R_{0}^{3} A\)
\(\text { Nuclear density, } \rho_{\mathrm{nu}}=\frac{\text { Mass of nucleus }}{\text { Volume of nucleus }} \text { or } \rho_{\mathrm{nu}}=\frac{m A}{\frac{4}{3} \pi R_{0}^{3} A}=\frac{3 m}{4 \pi R_{0}^{3}}\)
Clearly, nuclear density is independent of mass number A or the size of the nucleus. The nuclear mass density is of the order 1017 kg m-3. This density is very large as compared to the density of ordinary matter, say water, for which p = 1.0 x 103 kg m-3.
(i) The nuclear radius of \({ }_{8}^{16} \mathrm{O}\) is 3 X 10-15 m. The density of nuclear matter is(a) 2.9 x 1034 kg m-3 (b) 1.2 x 1017kg m-3 (c) 16 x 1027kg m-3 (d) 2.4 x 1017kg m-3 (ii) What is the density of hydrogen nucleus in SI units? Given Ro = 1.1 fermi and mp = 1.007825 amu
(a) 2.98 x 1017kg m-3 (b) 3.0 x 1034 kg m-3 (c) 1.99 x 1011 kg m-3 (d) 7.85 x 1017kg m-3 (iii) Density of a nucleus is
(a) more for lighter elements and less for heavier elements. (b) more for heavier elements and less for lighter elements (c) very less compared to ordinary matter (d) a constant (iv) The nuclear mass of \({ }_{26}^{56} \mathrm{Fe}\) is 55.85 amu. The its nuclear density is
(a) 5.0 x 1019kg m-3. (b) 1.5 x 1019kg m-3 (c) 2.9 x 1017kg m-3 (d) 9.2 x 1026kg m-3 (v) If the nucleus of \({ }_{13}^{27} \mathrm{Al}\) has a nuclear radius of about 3.6 fm, then \({ }_{52}^{125} \mathrm{Te}\) would have its radius approximately as
(a) 9.6 fm (b) 12 fm (c) 4.8 fm (d) 6 fm (a) -
From Bohr's atomic model, we know that the electrons have well defined energy levels in an isolated atom. But due to interatomic interactions in a crystal, the electrons of the outer shells are forced to have energies different from those in isolated atoms. Each energy level splits into a number of energy levels forming a continuous band.The gap between top of valence band and bottom of the conduction band in which no allowed energy levels for electrons can exist is called energy gap.
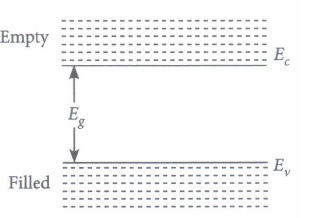
(i) In an insulator energy band gap is(a) Eg = 0 (b) Eg< 3eV (c) Eg > 3eV (d) None of the above (ii) In a semiconductor, separation between conduction and valence band is of the order of
(a) 0 eV (b) 1 eV (c) 10 eV (d) 50 eV (iii) Based on the band theory of conductors, insulators and semiconductors, the forbidden gap is smallest in
(a) conductors (b) insulators (c) semiconductors (d) All of these (iv) Carbon, silicon and germanium have four valence electrons each. At room temperature which one of the following statements is most appropriate?
(a) The number of free electrons for conduction is significant only in Si and Ge but small in C. (b) The number of free conduction electrons is significant in C but small in Si and Ge. (c) The number of free conduction electrons is negligibly small in all the three. (d) The number offree electrons for conduction is significant in all the three. (v) Solids having highest energy level partially filled with electrons are
(a) semiconductor (b) conductor (c) insulator (d) none of these (a) -
Solar cell is a p-n junction diode which converts solar energy into electric energy. It is basically a solar energy converter. The upper layer of solar cell is of p- type semiconductor and very thin so that the incident light photons may easily reach the p-n junction. On the top face of p-layer, the metal finger electrodes are prepared in order to have enough spacing between the fingers for the lights to reach the p-n junction through p-layer.
(i) The schematic symbol of solar cell is
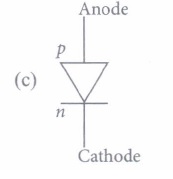
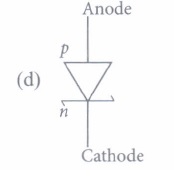
(ii) The p-n jqnction which generates an emf when solar radiations fall an it, with no external bias applied,is a
(a) light emitting diode (b) photodiode (c) solar cell (d) None of these (iii) For satellites the source of energy is
(a) Solar cell (b) Fuel cell (c) Edison cell (d) None of these (iv) Which of the following material is used in solar cell?
(a) Barium (b) Silicon (c) Silver (d) Selenium (v) The efficiency of a solar cell may be in the range
(a) 2 to 5% (b) 10 to 15% (c) 30 to 40% (d) 70 to 80% (a)
Part A
*****************************************
CBSE 12th Standard Physics Subject Case Study Questions With Solution 2021 Part - I Answer Keys
-
(i) (b): The proportionality constant k depends on the nature of the medium between the two charges.
(ii) (c): \({ As, }\left[\varepsilon_{0}\right]=\frac{1}{4 \pi F} \cdot \frac{q_{1} q_{2}}{r^{2}} =\frac{[\mathrm{AT}]^{2}}{\left[\mathrm{M} \mathrm{L} \mathrm{T}^{-2}\right]\left[\mathrm{L}^{2}\right]} \)
\(=\left\lfloor\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{~A}^{2}\right]\)
(iii) (b)
(iv) (d): \(F=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{d^{2}}\)
\(\therefore\left(10 \times 10^{-3}\right) \times 10=\frac{\left(9 \times 10^{9}\right) \times q^{2}}{(0.6)^{2}}\)
\(\text { or } \ q^{2}=\frac{10^{-1} \times 0.36}{9 \times 10^{9}}=4 \times 10^{-12}\)
\(\text { or } \ q=2 \times 10^{-6} \mathrm{C}=2 \mu \mathrm{C}\)
(v) (b) -
(I) (c) : As \(\frac{-d V}{d r}=E_{r}\) the negative of the slope of V versus r curve represents the component of electric field along r. Slope of curve is zero only at point 3. Therefore, the electric field vector is zero at point 3.
(ii) (a) : Near positive charge, net potential is positive and near a negative charge, net potential is negative. Thus, charge Q1 is positive and Q2 is negative.
(iii) (b) : From the figure, it can be seen that net potential due to two charges is positive everywhere in the region left to charge Q1. Therefore the magnitude of potential due to charge Q1 is greater than due to Q2.
(iv) (b)
(v) (c) : It can be seen that potential at the points both A and B are zero. When the charge is moved from A to B, work done by the electric field on the charge will be zero.
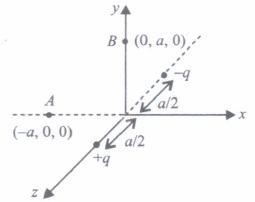
-
(i) (b)
(ii) (b): As \(I=\frac{\varepsilon}{R+r}\)
In first case,\(I=0.5 \mathrm{~A} ; R=12 \Omega\)
\(0.5=\frac{\varepsilon}{12+r} \Rightarrow \varepsilon=6.0+0.5 r\) ....(i)
In second case \(I=0.25 \mathrm{~A} ; R=25 \Omega\)
\(\varepsilon=6.25+0.25 r\) ...(ii)
From equation (i) and (ii), r = \(1 \Omega\)
(iii) (b)
(iv) (a): Current in the circuit \(I=\frac{E}{R+r}\)
Power delivered to the resistance R is
\(P=I^{2} R=\frac{E^{2} R}{(R+r)^{2}}\)
It is maximum when \(\frac{d P}{d R}=0\)
\(\frac{d P}{d R}=E^{2}\left[\frac{(r+R)^{2}-2 R(r+R)}{(r+R)^{4}}\right]=0\)
\(\text { or } \quad(r+R)^{2}=2 R(r+R) \text { or } R=r\)
(v) (b): For first case, \(\frac{\varepsilon}{R+r}=\frac{10}{R}\) ...(i)
For second case, \(\frac{\varepsilon}{5 R+r}=\frac{30}{5 R}\)
Dividing (i) by (ii), we get r = 5R
From (i), \(\frac{E}{R+5 R}=\frac{10}{R}\)
E = 60 V -
(i) (d)
(ii) (a): Using \(q v B \sin \theta=\frac{m v^{2}}{r}\)
\(r \propto \frac{1}{\sin \theta}\) for the same values of m, v, q and B
\(\therefore \frac{r_{A}}{r_{B}}=\frac{\sin 90^{\circ}}{\sin 30^{\circ}}=2 \text { or } r_{A}=2 r_{B} \text { or } r_{B}<r_{A}\)
(iii) (d): The radius of the helical path of the electron in the uniform magnetic field is
\(r=\frac{m v_{\perp}}{e B}=\frac{m v \sin \theta}{e B}=\frac{\left(2.4 \times 10^{-23} \mathrm{~kg} \mathrm{~m} / \mathrm{s}\right) \times \sin 30^{\circ}}{\left(1.6 \times 10^{-19} \mathrm{C}\right) \times 0.15 \mathrm{~T}}\)
\(=5 \times 10^{-4} \mathrm{~m}=0.5 \times 10^{-3} \mathrm{~m}=0.5 \mathrm{~mm}\)
(iv) (c): Here \(\vec{B}=8.35 \times 10^{-2} \hat{i} \mathrm{~T}\)
\(\vec{v}=2 \times 10^{5} \hat{i}+4 \times 10^{5} \hat{j} \mathrm{~m} / \mathrm{s}, m=1.67 \times 10^{-27} \mathrm{~kg}\)
Pitch of the helix (i.e., the linear distance moved along the magnetic field in one rotation) is given by
Pitch of the helix \(=\frac{2 \pi m v_{\|}}{q B}\)
\(=\frac{2 \times 3.14 \times 1.67 \times 10^{-27} \times 2 \times 10^{5}}{1.6 \times 10^{-19} \times 8.35 \times 10^{-2}}=0.157 \mathrm{~m}\)
(v) (b): Period of revolution
\(T=\frac{2 \pi R}{v \sin \theta} \Rightarrow T=\frac{2 \pi\left(\frac{m v \sin \theta}{q B}\right)}{v \sin \theta} \Rightarrow T=\frac{2 \pi m}{q B}\)
\(\therefore \text { Frequency, } v=\frac{1}{T}=\frac{q B}{2 \pi m}\) -
(i) (b): According to Gauss's law in magnetism \(\oint \vec{B} \cdot \overrightarrow{d S}=0\) which implies that number of magnetic field lines entering the Gaussian surface is equal to the number of magnetic field lines leaving it. Therefore, case (ii) is not possible.
(ii) (a): The net magnetic flux through a closed surface will be zero, i.e. \(\oint \vec{B} \cdot d \vec{s}=0\) because there are no magnetic monopoles.
(iii) (b)
(iv) (c): Gauss's law indicates that there are no sources or sinks of the magnetic field inside a closed surface. In other words, there a~e no free magnetic charges.
(v) (d): The surface integral of a magnetic field over a surface gives magnetic flux through that surface. -
(i) (c) :The mutual inductance ofthe system is \(M=\mu_{0} n_{1} n_{2} \pi a^{2} L\)
(ii) (c): Here \(\phi_{B}=2 \times 10^{-2} \mathrm{~Wb}, I=0.01 \mathrm{~A}\)
As \(\phi_{B}=M I\)
\(\therefore\) Mutual inductance between two coils is \(M=\frac{\phi_{B}}{I}=\frac{2 \times 10^{-2} \mathrm{~Wb}}{0.01 \mathrm{~A}}=2 \mathrm{H}\)
(iii) (b) : Mutual inductance of coils \(M=\frac{\mu_{0} \mu_{r} N_{1} N_{2} A}{l}\)
It is clear that mutual inductance of coils can be increased by increasing the number of turns in the coils.
(iv) (a) : We know that the mutual inductance depends (directly proportional) on the permeability of the medium surrounding the coils. When the permeability of the medium is increased by inserting a sheet of iron, then the mutual inductance between the coils also increases.
(v) (c) -
(I) (b): Inductance, L = 80 mH = 80 x 10-3 H
Capacitance, C = \(60 \mu \mathrm{F}=60 \times 10^{-6} \mathrm{~F}, V=230 \mathrm{~V}\)
Frequency, u = 50 Hz
\(\omega=2 \pi v=100 \pi \mathrm{rad} \mathrm{s}^{-1}\)
Peak voltage \(V_{0}=V \sqrt{2}=230 \sqrt{2} \mathrm{~V}\)
Maximum current is given by, \(I_{0}=\frac{V_{0}}{\left(\omega L-\frac{1}{\omega C}\right)}\)
\(I_{0}=\frac{230 \sqrt{2}}{\left(100 \pi \times 80 \times 10^{-3}-\frac{1}{100 \pi \times 60 \times 10^{-6}}\right)}\)
Amplitude of maximum current, Io = 11.63 A
(ii) (c): rms value of current,
\(I=\frac{I_{0}}{\sqrt{2}}=\frac{-11.63}{\sqrt{2}}=-8.23 \mathrm{~A}\)
Negative sign appears as \(\omega L<\frac{1}{\omega C}\)
(iii) (a): Average power consumed by the inductor is zero because of phase difference of \(\frac{\pi}{2}\) between voltage and current through inductor.
(iv) (b): Average power consumed by the capacitor is zero because of phase difference of \(\frac{\pi}{2}\) between voltage and current through capacitor
(v) (a) -
(i) (d): Given \(\vec{B}=B_{0} \sin (k x+\omega t) \hat{j} \mathrm{~T}\)
The relation between electric and magnetic field is,
\(c-\frac{E}{B} \text { or } E-c B\)
The electric field component is perpendicular to the direction of propagation and the direction of magnetic field. Therefore, the electric field component along z-axis is obtained as
\(\vec{E}=c B_{0} \sin (k x+\omega t) \hat{k} \mathrm{~V} / \mathrm{m}\)
(ii) (c): \(\frac{d E}{d z}=-\frac{d B}{d t}\)
\(\frac{d E}{d z}=-2 E_{0} k \sin k z \cos \omega t=-\frac{d B}{d t} \)
\(d B=+2 E_{0} k \sin k z \cos \omega t d t \)
\(B=+2 E_{0} k \sin k z \int \cos \omega t d t=+2 E_{0} \frac{k}{\omega} \sin k z \sin \omega t \)
\(\frac{E_{0}}{B_{0}}=\frac{\omega}{k}=c \)
\(B=\frac{2 E_{0}}{c} \sin k z \sin \omega t \ \therefore \ \vec{B}=\frac{2 E_{0}}{c} \sin k z \sin \omega t \hat{j}\)
E is along y-direction and the wave propagates along x-axis,
\(\therefore\) B should be in a direction perpendicular to both x-and y-axis
(iii) (d): Here, \(E=6.3 \hat{j} ; c=3 \times 10^{8} \mathrm{~m} / \mathrm{s}\)
The magnitude of B is
\(B_{z}=\frac{E}{c}=\frac{6.3}{3 \times 10^{8}}=2.1 \times 10^{-8} \mathrm{~T}=0.021 \mu \mathrm{T}\)
(iv) (d): Here, \(E_{0}=66 \mathrm{Vm}^{-1}, E_{y}=66 \cos \omega\left(t-\frac{x}{c}\right)\)
\(\lambda=3 \mathrm{~mm}=3 \times 10^{-3} \mathrm{~m}, k=\frac{2 \pi}{\lambda} \)
\(\frac{\omega}{k}=c \Rightarrow \omega=c k=3 \times 10^{8} \times \frac{2 \pi}{3 \times 10^{-3}} \)
\(\text {or } \ \omega=2 \pi \times 10^{11} \)
\(\therefore \quad E_{y}=66 \cos 2 \pi \times 10^{11}\left(t-\frac{x}{c}\right) \)
\(B_{z}=\frac{E_{y}}{c}=\left(\frac{66}{3 \times 10^{8}}\right) \cos 2 \pi \times 10^{11}\left(t-\frac{x}{c}\right) \)
\(=2.2 \times 10^{-7} \cos 2 \pi \times 10^{11}\left(t-\frac{x}{c}\right)\)
(v) (a): At a particular point, E = 9.3 V m-1
\(\therefore\) Magnetic iel at the same point \(=\frac{9.3}{3 \times 10^{8}}\)
= 3.1 x 10-8 T -
(i) (b): Here, \(f_{0}=2.0, f_{e}=6.25 \mathrm{~cm}, u_{0}=?\)
When the final image is obtained at the least distance of distinct vision:
Ve = - 25 cm
\(\text {As } \frac{1}{v_{e}}-\frac{1}{u_{e}}=\frac{1}{f_{e}} \)
\(\therefore \ \frac{1}{u_{e}}=\frac{1}{v_{e}}-\frac{1}{f_{e}}=\frac{1}{-25}-\frac{1}{6.25} \)
\(=\frac{-1-4}{25}=\frac{-5}{25}=-\frac{1}{5} \)
\(\text {or } u_{e}=-5 \mathrm{~cm}\)
(ii) (b): Distance between objective and eye-piece = 15cm
\(\therefore\) Distance of the image from objective is
\(v_{0}=15-5=10 \mathrm{~cm} \)
\(\therefore \quad \frac{1}{u_{0}}=\frac{1}{v_{0}}-\frac{1}{f_{0}}=\frac{1}{10}-\frac{1}{2}=\frac{1-5}{10}=-\frac{2}{5} \)
\(\text {or } \ u_{0}=-\frac{5}{2}=-2.5 \mathrm{~cm}\)
\(\therefore\) Distance of object from objective = 2.5 cm
(iii) (a): Magnifying power
\(m=m_{0} \times m_{e}=\frac{v_{0}}{u_{0}}\left(1+\frac{D}{f_{e}}\right)=\frac{10}{2.5}\left(1+\frac{25}{6.25}\right)=20\)
(iv) (a): The intermediate image formed, by the objective of a compound microscope is real, inverted and magnified.
(v) (d) -
(i) (c) : Here \(d=0.1 \mathrm{~mm}, \lambda=6000 \dot A, D=0.5 \mathrm{~m}\)
For third dark band \(d \sin \theta=3 \lambda ; \sin \theta=\frac{3 \lambda}{d}=\frac{y}{D}\)
\(y=\frac{3 D \lambda}{d}=\frac{3 \times 0.5 \times 6 \times 10^{-7}}{0.1 \times 10^{-3}}=9 \times 10^{-3} \mathrm{~m}=9 \mathrm{mn}\)
(ii) (b): Given \(d=0.2 \mathrm{~mm}=0.2 \times 10^{-3} \mathrm{~m}, D=2 \mathrm{~m}\)
\(\lambda=5000 \dot A=5 \times 10^{-7} \mathrm{~m}\)
The distance between the first minimum on other side of the central maximum
\(x=\frac{2 \lambda D}{d}=\frac{2 \times 5 \times 10^{-7} \times 2}{0.2 \times 10^{-3}} \Rightarrow x=10^{-2} \mathrm{~m}\)
(iii) (a): Here \(\lambda=600 \mathrm{nm}=6 \times 10^{-7} \mathrm{~m}\)
\(a=0.2 \mathrm{~mm}=2 \times 10^{-4} \mathrm{~m}, \theta=?\)
Angular width of central maxima
\(\theta=\frac{2 \lambda}{a}=\frac{2 \times 6 \times 10^{-7}}{2 \times 10^{-4}}=6 \times 10^{-3} \mathrm{rad}\)
(iv) (d) : When red light is replaced by blue light (\(\lambda\)B < \(\lambda\)R) the diffraction pattern bands becomes narrow and crowded together.
(v) (b) : To observe diffraction, the size of the obstacle should be of the order of wavelength. -
(i) (d): Power of light received by the cone \(=I\left(\pi R^{2}\right)\)
Let number of photons hitting the cone per second is n.
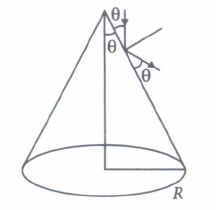
Then, \(n E=I \pi R^{2} \Rightarrow n=\pi R^{2} I / E\)
(ii) (b): Initial moment \(p_{i}=\frac{E}{c}\)
For a perfectly selecting surface
Final momentum \(p_{f}=\frac{-E}{c}\)
\(\Delta p=p_{f}-p_{i}=\frac{-E}{c}-\frac{E}{c}=\frac{-2 E}{c}\)
Hence a momentum \(\frac{2 E}{c}\) is transferred to the reflecting surface.
(iii) (a): According to the theory of relatively,
\(E=m c^{2}=m c . c=p c\)
\(\text { or } \quad E^{2}=p^{2} c^{2}\)
where p is the momentum of a photon.
(iv) (b): I = 1 kWm-2
As, 50% of light is reflected, thus e = 0.5
Radiation pressure \(P=\frac{(1+e) I}{c}\)
\(\therefore \quad P=\frac{(1+0.5) \times 1000}{3 \times 10^{8}}=5 \times 10^{-6} \mathrm{~Pa}\)
(v) (a) : \(\frac{P_{\mathrm{rad}}}{P_{0}}=\frac{5 \times 10^{-6}}{1 \times 10^{5}}=5 \times 10^{-11}\) -
(i) (b): \(\text { On other planet }: m v r=2 n \frac{h}{2 \pi} \Rightarrow v=\frac{n h}{\pi m r}\)
\(\frac{m v^{2}}{r}=\frac{1}{4 \pi \varepsilon_{0}} \frac{e^{2}}{r^{2}} \Rightarrow \frac{m n^{2} h^{2}}{n^{2} m^{2} r^{3}}=\frac{1}{4 \pi \varepsilon_{0}} \frac{e^{2}}{r^{2}}\)
Putting n = 1, we get r \( =\frac{4 h^{2} \varepsilon_{0}}{m \pi e^{2}}\)
(ii) (b): \(\text {On our planet: } v_{0}=\frac{e^{2}}{2 \varepsilon_{0} n h}\)
\(\text {On other planet : } v=\frac{e^{2}}{2 \varepsilon_{0}(2 n) h}=\frac{v_{0}}{2}\)
(iii) (b): On our planet \(E_{n}=-\frac{13.6}{n^{2}}\)
On other planet \(E_{n}^{\prime}=-\frac{13.6}{(2 n)^{2}}\)
\(\Rightarrow \quad E_{n}^{\prime}=\frac{E_{n}}{4}=-3.4 \mathrm{eV}\)
(iv) (c): Centripetal acceleration = mv2/r Further, as n increases, r also increases. Therefore, centripetal acceleration for n = 2 is less than that for n = 1. So, statement (i) is wrong. Statement (ii) and (iii) are correct.
(v) (c): Potential energy = -C/r2 and total energy = -Rhc/n2. With higher orbit, both rand n increase. So, both become less negative; hence both increase. -
(i) (d) : Here R = 3 X 10-15 m
Nuclear mass = 16 amu = 16 x 1.66 x 10-27 kg
\(\rho_{\mathrm{nu}}=\frac{\text { Nuclear mass }}{\text { Nuclear volume }}=\frac{16 \times 1.66 \times 10^{-27}}{\frac{4}{3} \pi\left(3 \times 10^{-15}\right)^{3}}\)
\(=2.359 \times 10^{17} \mathrm{~kg} \mathrm{~m}^{-3} \simeq 2.4 \times 10^{17} \mathrm{~kg} \mathrm{~m}^{-3}\)
(ii) (a): Density,
\(\rho=\frac{3 m_{p}}{4 \pi R_{0}^{3}}=\frac{3 \times 1.007825 \times 1.66 \times 10^{-27}}{4 \times \frac{22}{7} \times\left(1.1 \times 10^{-15}\right)^{3}}\)
\(=2.98 \times 10^{17} \mathrm{~kg} \mathrm{~m}^{-3}\)
(iii) (d) : \(\text { Density }=\frac{\text { Mass }}{\text { Volume }}=\frac{A m_{p}}{\frac{4}{3} \pi\left(R_{o} A^{1 / 3}\right)}\)
\(=\frac{m_{p}}{\frac{4}{3} \pi R_{0}^{3}}\)
\(\text { where } m_{P}=1.6 \times 10^{-27} \mathrm{~kg}^{3}\)
\(=2.3 \times 10^{17} \mathrm{~kg} \mathrm{~m}^{-3} \text {, which is a constant }\)
(iv) (c): Given, mass of mFe = 55.85 amu
= 55.85 x 1.66 x 10-27 kg = 9.27 x 10-26 kg
Nuclear radius = \(R_{0} A^{1 / 3}=1.1 \times 10^{-15} \times(56)^{1 / 3} \mathrm{~m}\)
\(\rho_{\mathrm{nu}}=\frac{\text { Nuclear mass }}{\text { Nuclear volume }}=\frac{m_{\mathrm{Fe}}}{\frac{4}{3} \pi R^{3}}\) \([\because A=56]\)
\(=\frac{9.27 \times 10^{-26}}{\frac{4 \pi}{3} \times\left(1.1 \times 10^{-15}\right)^{3} \times 56}=2.9 \times 10^{17} \mathrm{~kg} \mathrm{~m}^{-3}\)
(v) (d): Here, A1 = 27, A2 = 125, R1 = 3.6 fm
\(\text { As, } \frac{R_{2}}{R_{1}}=\left(\frac{A_{2}}{A_{1}}\right)^{1 / 3}=\left(\frac{125}{27}\right)^{1 / 3}=\frac{5}{3}\)
\(\therefore \quad R_{2}=\frac{5}{3} R_{1}=\frac{5}{3} \times 3.6=6 \mathrm{fm}\) -
(i) (c) :In insulator, energy band gap is > 3 eV
(ii) (b) : In conductor, separation between conduction and valence bands is zero and in insulator, it is greater than 1 eV. Hence in semiconductor the separation between conduction and valence band is 1 eV.
(iii) (a): According to band theory the forbidden gap in conductors Eg = 0, in insulators Eg > 3 eV and in semiconductors Eg < 3 eV.
(iv) (a): The four valence electrons of C, Si and Ge lie respectively in the second, third and fourth orbit.Hence energy required to take out an electron from these atoms (i.e. ionisation energy Eg) will be least for Ge, followed by Si and highest for C. Hence, the number of free electrons for conduction in Ge and Si are significant but negligibly small for C.
(v) (b) -
(i) (a)
(ii) (c)
(iii) (a) : Solar cells are the source of energy for satellites.
(iv) (b) : Silicon is used in solar cell.
(v) (b) : 10 to 15%.
Part A






































