CBSE 12th Standard Physics Subject Electric Charges And Fields Chapter Case Study Questions With Solution 2021
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 12 , and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Physics Subject Electric Charges And Fields Case Study Questions With Solution 2021
12th Standard CBSE
-
Reg.No. :
Physics
-
Coulomb's law states that the electrostatic force of attraction or repulsion acting between two stationary point charges is given by
\(F=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{r^{2}}\)

where F denotes the force between two charges q1 and q2 separated by a distance r in free space, Eo is a constant known as permittivity of free space. Free space is vacuum and may be taken to be air practically.
If free space is replaced by a medium, then Eo is replaced by (Eok) or (EoEr)where k is known as dielectric constant or relative permittivity.
(i) In coulomb's law, F = \(k \frac{q_{1} q_{2}}{r^{2}}\), then on which of the following factors does the proportionality constant k depends?(a) Electrostatic force acting between the two charges (b) Nature of the medium between the two charges (c) Magnitude of the two charges (d) Distance between the two charges (ii) Dimensional formula for the permittivity constant Eo of free space is
\(\text { (a) }\left[\mathrm{ML}^{-3} \mathrm{~T}^{4} \mathrm{~A}^{2}\right]\) \(\text { (b) }\left[M^{-1} L^{3} T^{2} A^{2}\right]\) \(\text { (c) }\left[\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{~A}^{2}\right]\) \(\text { (d) }\left[M L^{-3} T^{4} A^{-2}\right]\) (iii) The force of repulsion between two charges of 1 C each, kept 1 m apart in vaccum is
\(\text { (a) } \frac{1}{9 \times 10^{9}} \mathrm{~N}\) \(\text { (b) }\left[M^{-1} L^{3} T^{2} A^{2}\right]\) \(\text { (c) } 9 \times 10^{7} \mathrm{~N}\) \(\text { (d) } \frac{1}{9 \times 10^{12}} \mathrm{~N}\) (iv) Two identical charges repel each other with a force equal to 10 mgwt when they are 0.6 m apart in air. (g = 10 ms-2). The value of each charge is
(a) 2 mC (b) 2 x10-7 mC (c) 2 nC (d) 2\(\mu \)C (v) Coulomb's law for the force between electric charges most closely resembles with
(a) law of conservation of energy (b) Newton's law of gravitation (c) Newton's 2nd law of motion (d) law of conservation of charge (a) -
In 1909, Robert Millikan was the first to find the charge of an electron in his now-famous oil-drop experiment. In that experiment, tiny oil drops were sprayed into a uniform electric field between a horizontal pair of oppositely charged plates. The drops were observed with a magnifying eyepiece, and the electric field was adjusted so that the upward force on some negatively charged oil drops was just sufficient to balance the downward force of gravity. That is, when suspended, upward force qE just equaled Mg. Millikan accurately measured the charges on many oil drops and found the values to be whole number multiples of 1.6 x 10-19 C the charge of the electron. For this, he won the Nobel prize.
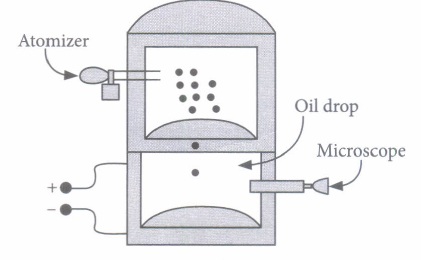
(i) If a drop of mass 1.08 x 10-14 kg remains stationary in an electric field of 1.68 x 105 N C-I, then the charge of this drop is(a) 6.40 x 10-19 C (b) 3.2 x 10-19 C (c) 1.6 X 10-19 C (d) 4.8 x 10-19 C (ii) Extra electrons on this particular oil drop (given the presently known charge of the electron) are
(a) 4 (b) 3 (c) 5 (d) 8 (iii) A negatively charged oil drop is prevented from falling under gravity by applying a vertical electric field 100 V m-1.If the mass of the drop is 1.6 X 10-3 g, the number of electrons carried by the drop is (g= 10 m s-2)
(a) 1018 (b) 1015 (c) 1012 (d) 109 (iv) The important conclusion given by Millikan's experiment about the charge is
(a) charge is never quantized (b) charge has no definite value (c) charge is quantized (d) charge on oil drop always increases. (v) If in Millikan's oil drop experiment, charges on drops are found to be \(8 \mu \mathrm{C}, 12 \mu \mathrm{C}, 20 \mu \mathrm{C}\) then quanta of charge is
\(\text { (a) } 8 \mu \mathrm{C}\) \(\text { (b) } 20 \mu \mathrm{C}\) \(\text { (c) } 12 \mu \mathrm{C}\) \(\text { (d) } 4 \mu \mathrm{C}\) (a) -
Gauss's law and Coulomb's law, although expressed in different forms, are equivalent ways of describing the relation between charge and electric field in static conditions. Gauss's law is \(\varepsilon_{0} \phi=q_{\text {encl }}\), when
qencl is the net charge inside an imaginary closed surface called Gaussian surface. \(\phi=\oint \vec{E} \cdot d \vec{A}\) gives the electric flux through the Gaussian surface. The two equations hold only when the net charge is in vacuum or air.
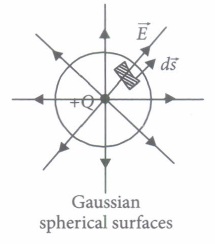
(I) If there is only one type of charge in the universe, then \((\vec{E} \rightarrow \text { Electric field, } d \vec{s} \rightarrow \text { Area vector })\)(a) \(\oint \vec{E} \cdot d \vec{s} \neq 0\) on any surface (b) \(\oint \vec{E} \cdot d \vec{s}\) could not be defined (c) \(\oint \vec{E} \cdot d \vec{s}=\infty\) if charge is inside (d) \(\oint \vec{E} \cdot d \vec{s}=0\) if charge is outside, \(\oint \vec{E} \cdot d \vec{s}=\frac{q}{\varepsilon_{0}}\) if charge is inside (ii) What is the nature of Gaussian surface involved in Gauss law of electrostatic?
(a) Magnetic (b) Scalar (c) Vector (d) Electrical (iii) A charge 10 \(\mu \)C is placed at the centre of a hemisphere of radius R = 10 cm as shown. The electric flux through the hemisphere (in MKS units) is

(a) 20 x 105 (b) 10 x 105 (c) 6 x 105 (d) 2 x 105 (iv) The electric flux through a closed surface area S enclosing charge Q is \(\phi\). If the surface area is doubled, then the flux is
\(\text { (a) } 2 \phi\) \(\text { (b) } \phi / 2\) \(\text { (c) } \phi / 4\) \(\text { (d) } \phi\) (v) A Gaussian surface encloses a dipole. 'The electric flux through this surface is
\(\text { (a) } \frac{q}{\varepsilon_{0}}\) \(\text { (b) } \frac{2 q}{\varepsilon_{0}}\) \(\text { (c) } \frac{q}{2 \varepsilon_{0}}\) (d) zero (a) -
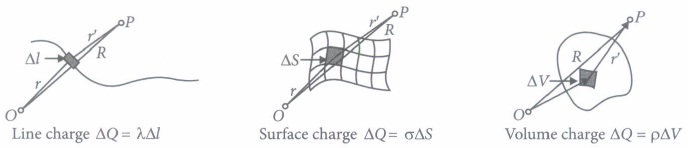
In practice, we deal with charges much greater in magnitude than the charge on an electron, so we can ignore the quantum nature of charges and imagine that the charge is spread in a region in a continuous manner. Such a charge distribution is known as continuous charge distribution. There are three types of continuous charge distribution : (i) Line charge distribution (ii) Surface charge distribution (iii) Volume charge distribution as shown in figure.
(I) Statement 1 : Gauss's law can't be used to calculate electric field near an electric dipole.
Statement 2 : Electric dipole don't have symmetrical charge distribution.(a) Statement 1 and statement 2 are true (b) Statement 1 is false but statement 2 is true (c) Statement 1 is true but statement 2 is false (d) Both statements are false (ii) An electric charge of 8.85 X 10-13 C is placed at the centre of a sphere of radius 1 m. The electric flux through the sphere is
(a) 0.2 N C-1 m2 (b) 0.1 N C-1 m2 (c) 0.3 N C-1 m2 (d) 0.01 N C-1 m2 (iii) The electric field within the nucleus is generally observed to be linearly dependent on r. So,
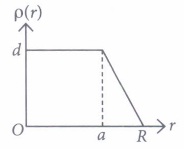
(a) a=O \(\text { (b) } a=\frac{R}{2}\) (c) a=-R \(\text { (d) } a=\frac{2 R}{3}\) (iv) What charge would be required to electrify a sphere of radius 25 cm so as to get a surface charge density of \(\frac{3}{\pi} \mathrm{C} \mathrm{m}^{-2} ?\)
(a) 0.75 C (b) 7.5 C (c) 75 C (d) zero (v) The SI unit of linear charge density is
(a) Cm (b) Cm-1 (c) C m-2 (d) C m-3 (a) -
Surface charge density is defined as charge per unit surface area of surface charge distribution. i.e., \(\sigma=\frac{d q}{d S}\) Two large. thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs having magnitude of 17.0 x 10-22 C m-2 as shown. The intensity of electric field at a point is \(E=\frac{\sigma}{\varepsilon_{0}}\) where \(\varepsilon_{0}\) = permittivity of free space.
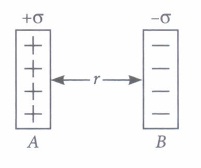
(i) E in the outer region of the first plate is\(\text { (a) } 17 \times 10^{-22} \mathrm{~N} / \mathrm{C}\) \(\text { (b) } 1.5 \times 10^{-25} \mathrm{~N} / \mathrm{C}\) \(\text { (c) } 1.9 \times 10^{-10} \mathrm{~N} / \mathrm{C}\) (d) zero (ii) E in the outer region of the second plate is
\(\text { (a) } 17 \times 10^{-22} \mathrm{~N} / \mathrm{C}\) \(\text { (b) } 1.5 \times 10^{-15} \mathrm{~N} / \mathrm{C}\) \(\text { (c) } 1.9 \times 10^{-10} \mathrm{~N} / \mathrm{C}\) (d) zero (iii) E between the plates is
\(\text { (a) } 17 \times 10^{-22} \mathrm{~N} / \mathrm{C}\) \(\text { (b) } 1.5 \times 10^{-15} \mathrm{~N} / \mathrm{C}\) \(\text { (c) } 1.9 \times 10^{-10} \mathrm{~N} / \mathrm{C}\) (d) zero (iv) The ratio of E from right side of B at distances 2 cm and 4 ern, respectively is
(a) 1: 2 (b) 2: 1 (c) 1: 1 \(\text { (d) } 1: \sqrt{2}\) (v) In order to estimate the electric field due to a thin finite plane metal plate, the Gaussian surface considered is
(a) spherical (b) cylindrical (c) straight line (d) none of these (a)
Part A
*****************************************
CBSE 12th Standard Physics Subject Electric Charges And Fields Case Study Questions With Solution 2021 Answer Keys
-
(i) (b): The proportionality constant k depends on the nature of the medium between the two charges.
(ii) (c): \({ As, }\left[\varepsilon_{0}\right]=\frac{1}{4 \pi F} \cdot \frac{q_{1} q_{2}}{r^{2}} =\frac{[\mathrm{AT}]^{2}}{\left[\mathrm{M} \mathrm{L} \mathrm{T}^{-2}\right]\left[\mathrm{L}^{2}\right]} \)
\(=\left\lfloor\mathrm{M}^{-1} \mathrm{~L}^{-3} \mathrm{~T}^{4} \mathrm{~A}^{2}\right]\)
(iii) (b)
(iv) (d): \(F=\frac{1}{4 \pi \varepsilon_{0}} \frac{q_{1} q_{2}}{d^{2}}\)
\(\therefore\left(10 \times 10^{-3}\right) \times 10=\frac{\left(9 \times 10^{9}\right) \times q^{2}}{(0.6)^{2}}\)
\(\text { or } \ q^{2}=\frac{10^{-1} \times 0.36}{9 \times 10^{9}}=4 \times 10^{-12}\)
\(\text { or } \ q=2 \times 10^{-6} \mathrm{C}=2 \mu \mathrm{C}\)
(v) (b) -
(i) (a): As, \(q E=m g \Rightarrow q=\frac{1.08 \times 10^{-14} \times 9.8}{1.68 \times 10^{5}}\)
\(=6.4 \times 10^{-19} \mathrm{C}\)
(ii) (a): \(q=n e \text { or } \Rightarrow n=\frac{6.4 \times 10^{-19}}{1.6 \times 10^{-19}}=4\)
(iii) (c) : For the drop to be stationary,
Force on the drop due to electric field = Weight of the drop
qE=mg
\(q=\frac{m g}{E}=\frac{1.6 \times 10^{-6} \times 10}{100}=1.6 \times 10^{-7} \mathrm{C}\)
Number of electrons carried by the drop is
\(n=\frac{q}{e}=\frac{1.6 \times 10^{-7} \mathrm{C}}{1.6 \times 10^{-19} \mathrm{C}}=10^{12}\)
(iv) (c)
(v) (d): Millikan's experiment confirmed that the charges are quantized, i.e., charges are small integer multiples of the base value which is charge on electron. The charges on the drops are found to be multiple of 4. Hence, the quanta of charge is 4 \(\mu \)C. -
(I) (d): If there is only one type of charge in the universe then it will produce electric field somehow. Hence Gauss's law is valid.
(ii) (c)
(iii) (c) : According to Gauss's theorem,
Electric flux through the sphere = \(\frac{q}{\varepsilon_{0}}\)
\(\therefore\) Electric flux through the hemisphere = \(\frac{1}{2} \frac{q}{\varepsilon_{0}}\)
= \(\frac{10 \times 10^{-6}}{2 \times 8.854 \times 10^{-12}}=0.56 \times 10^{6} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-1}\)
\(\approx 0.6 \times 10^{6} \mathrm{Nm}^{2} \mathrm{C}^{-1}=6 \times 10^{5} \mathrm{~N} \mathrm{~m}^{2} \mathrm{C}^{-1}\)
(iv) (d): As flux is the total number of lines passing through the surface, for a given charge, it is always the charge enclosed \(Q / \varepsilon_{0}\).If area is doubled, the flux remains the same.
(v) (d): As net charge on a dipole is \((-q+q)=0\)
Thus, when a gaussian surface encloses a dipole, as per Gauss's theorem, electric flux through the surface,
\(\oint \vec{E} \cdot d \vec{S}=\frac{q}{\varepsilon_{0}}=0\) -
(i) (a): Gauss's law is applicable for any closed surface. Gauss's law is most useful in situation where the charge distribution has spherical or cylindrical symmetry or is distributed uniformly over the plane.
Whereas electric dipole is a system of two equal and opposite point charges separated by a very small and finite distance.
So both statements are correct.
(ii) (b): According to Gauss's law, the electric flux through the sphere is
\(\phi=\frac{q_{\mathrm{in}}}{\varepsilon_{0}}=\frac{8.85 \times 10^{-13} \mathrm{C}}{8.85 \times 10^{-12} \mathrm{C}^{2} \mathrm{~N}^{-1} \mathrm{~m}^{-2}}=0.1 \mathrm{~N} \mathrm{C}^{-1} \mathrm{~m}^{2}\)
(iii) (c) : For uniformly volume charge density,
\(E=\frac{\rho r}{3 \varepsilon_{0}}\)
\(E \propto r\)
(iv) (a): r = 25 ern = 0.25 m \(\sigma=\frac{3}{\pi} \mathrm{C} / \mathrm{m}^{2}\)
As, \(\sigma=\frac{q}{4 \pi r^{2}} \Rightarrow q=4 \pi \times(0.25)^{2} \times \frac{3}{\pi}=0.75 \mathrm{C}\)
(v) (b): The line charge density at a point on a line is the charge per unit length of the line at that point
\(\lambda=\frac{d q}{d L}\)
Thus, the SI unit for \(\lambda \text { is } \mathrm{Cm}^{-1} \text {. }\) -
(i) (d):There are two plates A and B having surface charge densities,
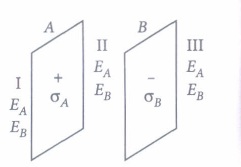
\(\sigma_{A}=17.0 \times 10^{-22} \mathrm{C} / \mathrm{m}^{2}\)
on A and \(\sigma_{B}=-17.0 \times 10^{-22} \mathrm{C} / \mathrm{m}^{2}\) on B, respectively.
According to Gauss' theorem, if the plates have same surface charge density but having opposite signs, then the electric field in region I is zero.
\(E_{\mathrm{I}}=E_{A}+E_{B}=\frac{\sigma}{2 \varepsilon_{0}}+\left(-\frac{\sigma}{2 \varepsilon_{0}}\right)=0\)
(ii) (d): The electric field in region III is also zero
\(E_{\mathrm{III}}=E_{A}+E_{B}=\frac{\sigma}{2 \varepsilon_{0}}+\left(-\frac{\sigma}{2 \varepsilon_{0}}\right)=0\)
(iii) (c) : In region II or between the plates, the electric field
\(E_{\mathrm{II}}=E_{A}-E_{B}=\frac{\sigma}{2 \varepsilon_{0}}+\frac{\sigma}{2 \varepsilon_{0}}\)
\(=\frac{\sigma\left(\sigma_{A} \text { or } \sigma_{B}\right)}{\varepsilon_{0}}=\frac{17.0 \times 10^{-22}}{8.85 \times 10^{-12}}\)
\(E=1.9 \times 10^{-10} \mathrm{~N} \mathrm{C}^{-1}\)
(iv) (c): Since, electric field due to an infinite-plane sheet of charge does not depend on the distance of observation point from the plane sheet of charge. So, for the given distances, the ratio of E will be 1 : 1.
(v) (b): In order to estimate the electric field due to a thin finite plane metal plate, we take a cylindrical cross-sectional area A and length 2r as the gaussian surface.
Part A






































