Class 11th Physics - Motion in a Plane Case Study Questions and Answers 2022 - 2023
By QB365 on 08 Sep, 2022
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 11 Physics Subject - Motion in a Plane, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
QB365 - Question Bank Software
Motion in a Plane Case Study Questions With Answer Key
11th Standard CBSE
-
Reg.No. :
Physics
-
Physical quantities are broadly classified into vectors and scalars. Physical quantities which have a sense of direction are known as vectors, these are categorised as polar and axial. Vectors cannot be added by simple laws of algebra but by adopting vector algebra. Resultant of two or more vectors could be zero depending upon their magnitude and direction. When resultant of three vectors are zero or null then Lami's theorem is applicable. Vector substraction is similar to addition where vector addition of one vector and negative vector of other is done. In our daily life vector addition and vector substraction is very important as far as application of mechanical force is concerned.
(i) Define vector physical quantity. Give example.
(ii) Distinguish between Polar and Axial vectors. Give example
(iii) What are unit vector and null vector?
(iv) State Lami's theorem of equilibrium of three vectors.
(v) State triangle law of vector addition.(a) -
An aeroplane is flying with velocity \(\vec{v}_{p}\) (= 100 ms-1) towards east, with respect to ground through motionless air and \(\vec{v}_{w}\) is the wind velocity with respect to ground. The total velocity of aeroplane is \(\vec{v}=\overrightarrow{v_{p}}+\overrightarrow{v_{w}}\). The magnitude of the velocity is often called speed. The heading of the plane is the direction in which the nose of the plane points. Infact, it is the direction in which the engine propels the plane. Resultant velocity and direction is the vector sum of different components of velocity, while relative velocity is the velocity of one with respect to another obtained by vector substraction.
(i) What is resultant velocity of plane if the wind velocity is towards south with respect to ground at 25 ms-1?
(ii) Define relative velocity? How it is determined?
(iii) If the wind blows with velocity 25 ms-1 northwards, then by which angle the plane velocity is deflected from east?
(iv) Vectors cannot be added algebraically. Why?
(v) Mention the condition when the magnitude of vectors \(\overline{\mathbf{A}}-\overline{\mathbf{B}}\)and \(\overline{\mathbf{A}}+\overline{\mathbf{B}}\) is same.(a) -
Projectile is the name given to a body thrown with some initial velocity with the horizontal direction and then allowed to move in two dimensions under the action of gravity alone, without being propelled by any engine or fuel. A projectile moves under the combined effect of two velocities: one a uniform velocity in the horizontal direction and other a uniformly changing velocity. It is observed that path of projectile which is known as trajectory is parabolic in shape.
(i) Does the time of flight, horizontal range and maximum height depend on the mass of the projectile?
(ii) State the relation between the maximum height attained by the projectile and the maximum range.
(iii) What is the angle between velocity and acceleration at the highest point of projectile path?
(iv) A body is projected with velocity u at angle e with the horizontal, what would be the angle and speed of projectile when it strike at the ground at same horizontal plane from which it is projected?
(v) What are the angles of projection for same initial velocity of projection at which horizontal range of the projectile is same?
(vi) Write the equation of the path of projectile, projected at angle e with initial velocity u, from a horizontal plane.(a) -
If a body moves in circle with a constant speed, then the magnitude of the velocity is constant but the direction of the velocity vector is changing all the time. Thusvelocity is changing with time. Therefore the motion of the body is accelerated. The acceleration is directed towards the centre of the circle and is called centripetal acceleration ac. If m is the mass of the body then the centripetal force is Fc = mac·
(i) What is effect on the linear momentum, angular momentum and kinetic energy of body, moving uniformly in circular path?
(ii) What is the magnitude and direction of ac of body moving in circular path of radius r with speed v?
(iii) A stone of mass m is tied to a string is whirled in circular path of radius r in horizontal plane at a constant speed v. What is the angle between velocity and acceleration? Also determine the tension in the string.
(iv) State the relation between linear velocity (v) and angular velocity (ω) of body moving in circular path of radius r,
(v) What would be the direction of motion of stone if at certain time its string get broken?
(vi) In a non-uniform circular motion with tangential acceleration at and radial acceleration ar. What would be the resultant acceleration?(a)
Case Study
*****************************************
Answers
Motion in a Plane Case Study Questions With Answer Key Answer Keys
-
(i) Physical quantity which have magnitude along with a sense of direction and must obey laws of vector algebra (addition) are known as vectors e.g., force, velocity, displacement etc.
(ii) Polar vectors: are those which have a starting point or point of application e.g., displacement. Axial vectors: These are those vectors which represent rotational effect and act along the axis of rotation in accordance with right-hand screw rule. e.g., angular velocity, torque, angular momentum.
(iii) Unit vector of a given vector is a vector of unit magnitude and has the same direction as that of the given vector \(\hat{A}=\frac{\vec{A}}{A}\)
While a null vector is the resultant of two equal and opposite vectors. It has arbitrary direction and zero magnitude.
(iv) Lami's theorem states that if three vectors acting at a point are in equilibrium then each vector is proportional to the sine of the angle between the other two vectors i.e.,
\(\frac{\mathrm{A}}{\sin \alpha}=\frac{\mathrm{B}}{\sin \beta}=\frac{\mathrm{C}}{\sin \gamma}\)
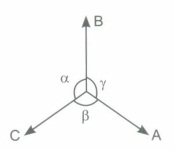
(v) It states that if two vectors acting on a particle at the same time are represented in magnitude and direction by the two sides of a triangle taken in same order then their resultant vector is represented in magnitude and direction by the third side of the triangle taken in opposite order. -
(i) Here vp = 100 ms-1 , vw = 25 ms-1, θ = 90
then total speed of plane \(v=\sqrt{v_{p}^{2}+v_{w}^{2}}=\sqrt{100^{2}+25^{2}}\) > 100 ms-1
(ii) Relative velocity of one body is with respect to other is obtained by vector subtraction. For example relative velocity of plane w.r.t. wind is \(\overrightarrow{v_{p w}}=\overrightarrow{v_{p}}-\overrightarrow{v_{w}}\).
(iii)
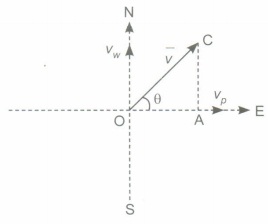
The resultant velocity of plane will be along OC, as shown
\( \tan \theta =\frac{\mathrm{AC}}{\mathrm{OA}}=\frac{v_{w}}{\mathrm{~V}_{p}}=\frac{25}{100} \)
\(\text { or } \quad \theta =\tan ^{-1} \frac{25}{100} \)
(iv) It is so because, the vectors possess direction as well as magnitude.
(v) \(\overline{\mathbf{A}}-\overline{\mathbf{B}}=\overline{\mathbf{A}}+\overline{\mathbf{B}}\), Magnitude is the same when θ between \(\overline{\mathrm{A}}\) and \(\overline{\mathrm{B}}\) is 90°.
\(\text { Since } R=\sqrt{A^{2}+B^{2} \pm 2 A B \cos \theta}\). -
(i) Projectile motion is independent of mass, it only depends on angle of projection and initial velocity of projection.
(ii) The maximum height attained by projectile is equal to one fourth of its maximum range.
(iii) At the highest point of projectile path the component of velocity becomes zero, therefore angle between acceleration acting vertically downward and horizontal component of velocity becomes 90°.
(iv) Since projectile follow a prabolic path, it strike back on same horizontal plane with same initial velocity and with same angle at which it was projected.
(v) At complimentary angles of projection i.e., θ and 90 - θ, the horizontal range is same.
(vi) \(y=x \tan \theta-\frac{g x^{2}}{2 u^{2} \cos ^{2} \theta}\) -
(i) Kinetic energy of body remain constant, while linear momentum and angular momentum change uniformly with respect to time.
(ii) \(a_{c}=\frac{v^{2}}{r},\) acting radialy toward centre of the circular path.
(iii) Velocity is tangential to path therefore it is perpendicular to acceleration acting radially toward centre. Tension in the string is equal to centripetal force \(T=\frac{m v^{2}}{r}\).
(iv) \(\vec{v}=\bar{w} \times \bar{r}\),i.e., angular velocity is perpendicular to plane of circular path and along the axis - as per right hand screw rule.
(v) Stone will move along tangent to the circular path, since velocity is along tangent to path.
(vi) \(a=\sqrt{a_{r}^{2}+a_{\mathrm{T}}^{2}}\), since \(\bar{a}_{r} \text { and } \bar{a}_{\mathrm{T}}\) are perpendicular to each other.
Case Study



































