Class 11th Physics - Work, Energy and Power Case Study Questions and Answers 2022 - 2023
By QB365 on 08 Sep, 2022
QB365 provides a detailed and simple solution for every Possible Case Study Questions in Class 11 Physics Subject - Work, Energy and Power, CBSE. It will help Students to get more practice questions, Students can Practice these question papers in addition to score best marks.
QB365 - Question Bank Software
Work, Energy and Power Case Study Questions With Answer Key
11th Standard CBSE
-
Reg.No. :
Physics
-
Mechanical energy exists in two forms: Kinetic energy and Potential energy. Kinetic energy is the energy possesed by a body by virtue of motion. Potential energy is the energy possessed by the body by virtue of its position or configuration. These two forms of energy are interconvertible. If no other form of energy is involved in a process, the sum of kinetic energy and potential energy always remains constant.
(i) State law of conservation of mechanical energy.
(ii) State two particles having mass m1 and m2 , both have equal linear momenta. What is the ratio of their kinetic energies?
(iii) Two particles of masses m1 and m2 have equal kinetic energies. What is the ratio of their linear momenta?
(iv) A particle of mass m has half the kinetic energy of another particle of mass m/2. If the speed of the heavier particle is increased by 2 ms-1, its new kinetic energy equals the original kinetic energy of the lighter particle. What is the ratio of the original speeds of the lighter and heavier Particle?
(v) A uniform rod of mass m and length I is made to stand vertically on one end. What is the potential energy of the rod in this position?
(vi) Give an example where a force does work on a body but fails to change its K-E.
(vii) Does K-E depend upon the direction of motion involved? Can it be negative? Does its value depend on frame of refrence?(a) -
Work is said to be done by a force acting on a body, provided the body is displaced actually in any direction except in a direction perpendicular to the direction of the force-mathematically, \(W=\bar{F} \cdot \bar{s}=F s \cos \theta\) whereas energy is the capacity of a body to do the work and Power is the rate at which the body do the work.
\(P=\frac{\mathrm{W}}{t}=\frac{\overline{\mathrm{F}} \cdot \bar{s}}{t}=\overline{\mathrm{F}} \cdot \bar{v}\)
Both, work and energy are measured in Joule while power is measured in watt.
(i) A box is pushed through 4.0 m across a floor offering 100 N resistance. Determine the work done by the applied force.
(ii) In the above question, determine the work done by the resistive force and by the gravity.
(iii) A truck draws a tractor of mass 1000 kg at a steady rate of 20 ms-1 on a level road. The tension in the coupling is 2000 N. What is the power spent on the tractor?
(iv) Determine the work done on the tractor in one minute?(a) -
The work done by a constant force acting on a body is given by \(W=\bar{F} \cdot \bar{r}, \text { where } \bar{F}\) is the force vector and \(\bar{r}\) is displacement vector. the displacement vector \(\bar{r}=\bar{r}_{2}-\bar{r}_{1}\) where r 1 is the initial position vector and \(\bar{r}_{2}\) is the final position vector. If the force is variable, the work done in moving a body from a Position \(\bar{r}\) to a position \(\bar{r}_{2}\) is given by \(W=\int_{v}^{r_{2}} \bar{F} \cdot d \bar{r}, \text { where } d \bar{r} \) is an infinitesimally small displacement.
(i) A particle is moved from a position \(\bar{r}_{1}=(3 \hat{i}+\)\(2 \hat{j}-4 \hat{k})\) metre to position \(\bar{r}_{2}=(5 \hat{i}+6 \hat{j}+9\)\(\hat{\boldsymbol{k}})\) metre under the action of a force \(\overline{\boldsymbol{F}}=\mathbf{(} \hat{\boldsymbol{i}}+\) \(\mathbf{3} \hat{\boldsymbol{j}}+\hat{\boldsymbol{k}})\) newton. Determine the net work done.
(ii) A body of mass m is projected from a tower of height h at angle \(\theta\) above the horizontal. Determine the workdone by the gravitational force during the time it takes to hit the ground.
(iii) A body of mass m is projected from the ground with a velocity u at an angle \(\theta\) above the horizontal. Determine the work done by the gravitational force in time \(t=\frac{u \sin \theta}{g}\)
(iv) In the above question if \(\theta\) = 45°, then determine the gravitational force in time t = \( \frac{2 u \sin \theta}{g} \)
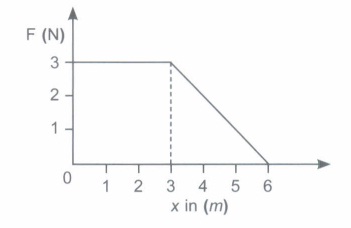
(v) A force F acting on an object varies with distance x as shown in Fig. Force is in Nand x is m. Determine the work done by the force in moving the object from x = 0 to x = 6 m.
(vi) The Potential energy of a 1kg particle free to move along the x-axis is given by \( V(x)=\left(\frac{x^{4}}{4}-\frac{x^{2}}{2}\right) \mathrm{J} \) .The total mechanical energy of the particle is 2J. Determine the maximum speed of the particle in m/s.(a) -
In a conservative force field, we can find the component of force from the potential energy at a point in the field. A positive force means repulsion and a negative force means attraction. From the given potential energy function U (r) we can find the equilibrium position where force is zero. Suppose the potential energy at a distance r from centre of the field is given as
\( \mathrm{U}(r)=\frac{A}{r^{2}}-\frac{B}{r} \)Where A and B are positive constants.
(i) What should be the nature of the field as per conclusion drawn from the form of given potential energy?
(ii) Determine the work done to move the particle from equilibrium to infinity.
(iii) If K.E of a body becomes 4 times of its initial value, then what would be new linear momentum?
(iv) Determine the percentage change in K.E of a body if momentum of a body increases by 0.01 %
(v) What does it meant by unstable equilibrium of a particle? Write condition for unstable equilibrium.
(vi) What are conservative forces?(a) -
A ball P moving with a velocity u strikes an identical stationary ball Q such that after the collision, the direction of motion of balls P and Q makes an angle 30° with the original direction of motion of ball P as shown.
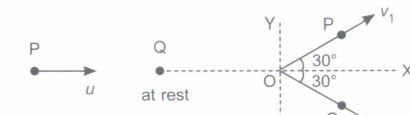
(i) Determine the speed V1 of ball P after collision.
(ii) Determine the ratio of the total kinetic energy of the balls after collision to that before collision.
(iii) Determine the ratio of velocity V1 and v 2 after the collision in terms of coefficient of restitution e.
(iv) A ball hits a floor and rebounds after an inelastic collision. What change would occur in total energy, kinetic energy and momentum of ball?(a)
Case Study
*****************************************
Answers
Work, Energy and Power Case Study Questions With Answer Key Answer Keys
-
(i) Total mechanical energy of a system is conserved if the forces doing work on it are conservative i.e., Individually kinetic energy K and the potential energy V(x) may vary from point to point, but their sum is constant throughout.
(ii) Since \(K=\frac{1}{2} m v^{2}=\frac{p^{2}}{2 m} ; \frac{K_{1}}{K_{2}}=\frac{m_{2}}{m_{1}}\)
(iii) Since Linear momentum \(p=\sqrt{2 m \mathrm{~K}}\)
\(\frac{p_{1}}{p_{2}}=\sqrt{\frac{m_{1}}{m_{2}}}\)
(iv) If v and v' be the original speed of the heavier and the lighter particles respectively.
\(\frac{1}{2} m v^{2}=\frac{1}{2} \times\left\{\frac{1}{2}\left(\frac{m}{2}\right) v^{\prime 2}\right\}\)
\(\therefore \ v^{2}=\frac{v^{\prime 2}}{4} \text { or } v^{\prime}=2 v\)
(v) Potential energy in the vertical position = work done is raising if from horizontal position to vertical position. Since the entire mass of the rod is concentrated at centre of mass which is raised through a height \(\frac{h}{2}\) therefore workdone = mgh = \(m g \frac{l}{2}\)
(vi) When a body is dragged on a rough horizontal surface with a constant velocity work is done against friction but K-E = constant.
(vii) No, Kinetic energy does not depend on the direction of motion and it K.E cannot be negative. The magnitude of K.E depends upon the frame of Refrence. -
(i) W = Fs cos \(\theta\) = 100 x 4 cos 0° = 400 J
(ii) Resistive force opposes the applied force. Box moves at 180o to the resistive force.
Therefore W = Fs .cos 180 = -400 J. Since motion is along horizontal and gravity is along the vertical, therefore workdone by gravity is
W = Fs cos 90 = zero.
(iii) Force applied = tension in coupling = 2000 N
As P = Fv cos\(\theta\) = 2000 x 20 cos 0 o = 40000W = 40 kW
(iv) Work done = Power x time = 40 kW x 60 s = 2400 kJ -
(i) Workdone \( W=\bar{F} \cdot \bar{r} \)
\( =\overline{\mathrm{F}} \cdot\left(\bar{r}_{2}-\bar{r}_{1}\right) \)
\( =(\hat{i}+3 \hat{j}+\hat{k}) \cdot[(5 \hat{i}+6 \hat{j}+9 \hat{k})-(3 \hat{i}+2 \hat{j}-4 \hat{k})] \)
\( =(\hat{i}+3 \hat{j}+\hat{k}) \cdot(2 \hat{i}+4 \hat{j}+13 \hat{k})=27 \mathrm{~J} \)
(ii) Net displacement from the time body is projected to the time it hits the ground is = h (vertically downwards)
\(\therefore\) work done W = mgh
(iii) For time \( t=\frac{u \sin \theta}{g} \) body attains the maximum height
\( h_{\max }=\frac{u^{2} \sin ^{2} \theta}{2 g} \)
therefore work done \( m g h_{\max }=\frac{m u^{2} \sin ^{2} \theta}{2} \)
(iv) Since during the time \( t=\frac{2 u \sin \theta}{g} \text { i.e. } \) the time of flight of projectile, displacement is zero, therefore workdone by gravitational force is zero.
(v) Workdone = Force x displacement
W = area enclosed by F-x curve from given figure
\( w=3 \times 3+\frac{1}{2} \times 3 \times 3=13.5 \mathrm{~J} \)
(vi) Velocity is maximum when K.E. is maximum for minimum P.E
\( \frac{d v}{d x}=0 \Rightarrow x^{2}-x=0 \)
\( \Rightarrow \quad x=\pm 1 \)
\( \text { P.E. }=\frac{1}{4}-\frac{1}{2}=\frac{-1}{4} \)
\( \mathrm{K} \cdot \mathrm{E}_{\max }+\mathrm{P.E}_{\min }=2 \)
\( \mathrm{K} \cdot \mathrm{E}_{\max }=2+\frac{1}{4}=\frac{9}{4} \)
\( \Rightarrow \quad \frac{1}{2} M v_{\max }^{2}=\frac{9}{4} \)
\( \Rightarrow \quad \frac{1}{2} \times 1 \times v_{\max }^{2}=\frac{9}{4} \)
\( \Rightarrow \quad v_{\max }=\frac{3}{\sqrt{2}} \mathrm{~m} / \mathrm{s} \) -
(i) The field is surely conservative
(ii) Work required can be calculated from P.E at the equilibrium position \( W=\frac{A}{r_{0}^{2}}-\frac{B}{r_{0}} \)where r0 - equilibrium position
At equilibrium \( r_{0}, \frac{d U}{d r}=0 \Rightarrow r_{0}=\frac{2 A}{B} \)
Therefore \( W=\frac{B^{2}}{4 A} . \)
(iii) Since K.E = p2/2M, when K.E becomes 4 times, p2 is 4 times therefore linear momentum P becomes 2 times.
(iv) Since \( \Delta P=M \Delta V=0.01 \% \)
\(\therefore\) \(\triangle\) V = 0.01%
Now \( \Delta E=\frac{1}{2} m(\Delta V)^{2} \)
\(\therefore\) \(\triangle\)E = 2 x 0.0 I = 0.02%
(v) In this a particle when displaced from equilibrium position, tends to move away from equilibrium position. potential energy V = maximum and \( \frac{d^{2} V}{d x^{2}} \) = negative.
(vi) When work done by against a force in displacing a particle does not depend upon the path along which particle is displaced, then such a force is known as conservative force. These forces keep the K.E constant and work done will be zero when particle is displaced in closed path. -
(i) From the conservation of X and Y components of linear momentum
mu = mv1 cos 30° + mv2 cos 30°
\( \Rightarrow \ u=\left(v_{1}+v_{2}\right) \frac{\sqrt{3}}{2} \)
and 0 = mv1 sin 30 - mV2 sin 30 \(\Rightarrow\) v1 = v2
\( v_{1}=\frac{u}{\sqrt{3}} \)
(ii) Total K.E before collision is \( \mathrm{K}_{i}=\frac{1}{2} m u^{2} \) and after collision \( \mathrm{K}_{f}=\frac{1}{2} m v_{1}^{2}+\frac{1}{2} m v_{2}^{2} \)
\( =\frac{1}{2} m\left(v_{1}^{2}+v_{2}^{2}\right)=\frac{1}{2} m\left(2 v_{1}^{2}\right)=\frac{m u^{2}}{3} \)
\( \frac{\mathrm{K}_{f}}{\mathrm{~K}_{i}}=\frac{2}{3} \)
(iii) \( e=\frac{v_{2}-v_{1}}{u_{1}-u_{2}}=0 \)
(iv) As the collision is inelastic, body loses some energy so that K.E of ball does not remain the same. However, total energy and total momentum of ball and earth system remain the same.
Case Study



































