- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Chemistry
-

Physics
-

Maths
-

Accountancy
-

Business Studies
-

Economics
-

Introductory Micro and Macroeconomics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Political Science
-

Engineering Graphics
-

Bio Technology
-

Entrepreneurship
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Psychology
-

Hindi Core
-

Tamil
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Physics
-

Mathematics
-

Chemistry
-

Biology
-

Economics
-

Business Studies
-

Accountancy
-

Computer Science
-

English
-

Geography
-

History
-

Physical Education
-

Psychology
-

Sociology
-

Bio Technology
-

Enterprenership
-

Hindi
-

Home Science
-

Political Science
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Social Science
-

Mathematics
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students
Model Paper 3mark
11th Standard
-
Reg.No. :
Physics
Time :
01:00:00 Hrs
Total Marks :
80
-
Explain what is meant by Cartesian coordinate system?
-
Define a vector. Give examples.
-
The Moon is orbiting the Earth approximately once in 27 days, what is the angle transversed by the Moon per day?
-
What is meant by frame of reference?
-
What is right handed coordinate system?
-
Does a scalar quantity depends upon the frame of reference chosen.
-
When the sum of two vectors is maximum?
-
Explain the addition of two vectors using components method.
-
Using components method, subtract the following vectors.
\(\overrightarrow { A } ={ A }_{ x }\hat { i } +{ A }_{ y }\hat { j } +{ A }_{ z }\hat { k } \)
\(\overrightarrow { B } ={ B }_{ x }\hat { i } +{ B }_{ y }\hat { j } +{ B }_{ z }\hat { k } \) -
What do you mean by multiplication of a vector by a real number?
-
What is position vector? Explain.
-
A vector \(\vec A\) is given as in the following figure. Find 4\(\vec A\) and -4\(\vec A\).
-
Given two vectors \(\vec A=2\hat i+4\hat j+5\hat k\) and \(\vec B=\hat i+3\hat j+6\hat k\). Find the product \(\vec A.\vec B\), and the magnitudes of \(\vec A\) and \(\vec B\) . What is the angle between them?
-
Compare the components for the following vector equations
(a) \(\vec F=m\vec a\)
(b) \(\vec p=0\) -
Determine the value of the T from the given vector equation \(5\hat j-T\hat j=6\hat j+3T\hat j\)
-
Suppose two cars A and B are moving with uniform velocities with respect to ground along parallel tracks and in the same direction. Let the velocities of A and B be 35 km h-1 due east and 40 km h-1 due east respectively. What is the relative velocity of car B with respect to A?
.png)
-
Suppose two trains A and B are moving with uniform velocities along parallel tracks but in opposite directions. Let the velocity of train A be 40 km h-1 due east and that of train B be 40 km h-1 due west. Calculate the relative velocities of the trains.
-
Consider two trains A and B moving along parallel tracks with the same velocity in the same direction. Let the velocity of each train be 50 km h-1 due east. Calculate the relative velocities of the trains.
-
What is idea proposed by Aristotle and Galileo about force?
-
State Newton's First Law.
-
Define inertia.
-
Why do passengers fall in backward direction when a bus suddenly starts moving from the rest position?
-
What is static friction? Explain
-
Draw the graph for the variation of both static and kinetic frictional forces with external applied force?
-
Define angle of friction?
-
A block of mass 2 kg rests on a plane inclined at an angle of 300 with the horizontal. The coefficient of friction between the block and the surface is 0.7. What will be the frictional force acting on the block?
-
A stone of mass 1kg is whirled in a circular path of radius 1m. Find out the tension in the string if the linear velocity is 10m/s.
-
Two masses m1 = 5 kg and m2 = 4 kg tied to a string are hanging over a light frictionless pulley. What is the acceleration of each mass when left free to move? (g = 10 ms-2).
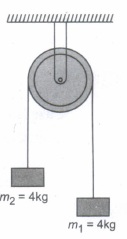
-
Three blocks of masses 10 kg, 7 kg and 2 kg are placed in contact with each other on a frictionless table. A force of 50 N is applied on the heaviest mass. What is the acceleration of the system?
-
Find the maximum speed at which a car can turn round a curve of 36 m radius on a level road. Given the coefficient of friction between the tyre and the road is 0.53.
-
Consider two objects of masses 5 kg and 20 kg which are initially at rest. A force 100 N is applied on the two objects for 5 second.
(a) What is the momentum gained by each object after 5s?
(b) What is the speed gained by each object after 5s? -
Obtain an expression for the power delivered by torque.
-
What is meant by rolling friction?
-
Calculate moment of inertia with respect to rotational axis xx' in following figures (a) and (b).
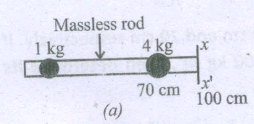
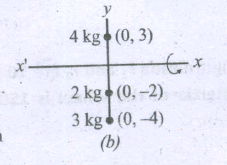
-
A ball tied to a string takes 4s to complete revolution along a horizontal circle. If by pulling the cord, the radius of the circle is reduced to half of the previous value, then how much time the ball will take in one revolution.
-
If angular momentum is conserved in a system whose moment of inertia is decreased, will its rotational kinetic energy be conserved?
-
The moment of inertia of two rotating bodies A and B are IA and IB ( CA> IB) and their angular momenta are equal. Which one has a greater kinetic energy?
-
A particle moves on a circular path with decreasing speed. What happens to its angular momentum?
-
Suppose unknowingly you wrote the universal gravitational constant value as G = 6.67\(\times\)1011 instead of the correct value G = 6.67\(\times\)1011, what is the acceleration due to gravity g' for this incorrect G? According to this new acceleration due to gravity, what will be your weight W'?
-
Calculate the gravitational field at point O due to three masses m1, m2 and m3 whose positions are given by the following figure. If the masses m1 and m2 are equal what is the change in gravitational field at the point O?
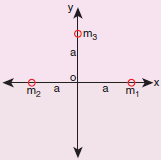
Part-A
Answer all the questions briefly
40 x 2 = 80






 11th Standard Physics Syllabus
11th Standard Physics Syllabus  11th Standard Physics Study Materials
11th Standard Physics Study Materials 11th Standard Physics MCQ Practise Tests
11th Standard Physics MCQ Practise Tests 

Reviews & Comments about 11th Physics Important Three Mark Question Paper 3
Write your Comment