Briefly explain the different types of errors and their causes with an example. How can these error be minimised?

Write the rules for "Rounding off" with example

The force F acting on a body moving in a circular path depends on mass of the body (m), velocity (v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method. (Take the value of k = 1)

Two resistors of resistances R₁= 150 ± 2 Ohm and R₂ = 220 ± 6 Ohm are connected in parallel combination. Calculate the equivalent resistance.
Hint:\(\frac{1}{R'}=\frac{1}{R_1}+\frac{1}{R_2}\)

A car moving uniform motion with speed 120 kmh^-2 is brought to a stop within a distance of 200 m. How long does it take for the car to stop?

The velocity time graph of a particle is given by

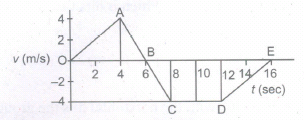
(i) Calculate distance and displacement of particle from given v-t graph.
(ii) Specify the time for which particle undergone acceleration, retardation and moves with constant velocity.
(iii) Calculate acceleration, retardation from given v-t graph.
(iv) Draw acceleration-time graph of given v-t graph.

Suppose an object is thrown with initial speed 10 ms^-1 at an angle \(\frac{\pi}{4}\) with the horizontal, what is the range covered? Suppose the same object is thrown similarly in the Moon, will there be any change in the range? If yes, what is the change? (The acceleration due to gravity in the Moon \(g_{moon}=\frac{1}{6}g\)).

Calculate the angle θ subtended by the two adjacent wooden spokes of a bullock cart wheel is shown in the figure. Express the angle in both radian and degree.

Explain the similarities and differences of centripetal and centrifugal forces.

Show how impulse force can be measured graphically.

Briefly explain how is a vehicle able to go round a level curved track. Determine the maximum speed with which the vehicle can negotiate this curved track safely.

An object of mass 10 kg moving with a speed of 15 ms^-1 hits the wall and comes to rest within
(a) 0.03 second
(b) 10 second.
Calculate the impulse and average force acting on the object in both the cases.

Explain with graphs the difference between work done by a constant force and by a variable force.

What is inelastic collision? In which way it is different from elastic collision. Mention few examples in day to day life for inelastic collision.

A particle of mass 2 kg moving with a velocity \({ v }_{ 1 }=(\overset { \wedge }{ 2i } -\overset { \wedge }{ 3j } )m/s\) experience a perfectly inelastic collision with another particle of mass 2 kg having velocity \({ v }_{ 2 }=(\overset { \wedge }{ 3i } -\overset { \wedge }{ 6k } )m/s\). Find the velocity and speed of the particle formed.

Discuss the force - displacement graph for a spring.

Define angular momentum and derive the expression of it.

A car of mass 1200 kg is travelling around a circular path of radius 300 m with a constant speed of 54 km/h. Calculate its angular momentum.

A solid sphere is undergoing pure rolling. What is the ratio of its translational kinetic energy to rotational kinetic energy?

Consider a thin uniform circular ring rolling down in an inclined plane without slipping. Compute the linear acceleration along the inclined plane if the angle of inclination is \(45 ^{0}\).

Explain the freely falling apple on Earth using the concept of gravitational potential V(r)?

Drive the relation between g & Gravitational constant.

Moon and an apple are accelerated by the same gravitational force due to Earth. Compare the acceleration of the two.

Find out the value of g' in your school laboratory?

Derive the expression for the terminal velocity of a sphere moving in a high viscous fluid using stokes force.

State and prove Bernoulli’s theorem for a flow of incompressible, non-viscous, and streamlined flow of fluid.

What is the effect of pressure on the boiling point of a liquid. Describe a simple experiment to demonstrate the boiling of H₂O at a temperature much lower than 100°C. Give a practical application of this phenomenon.

If a ball of skeel (density p =7.8 g cm^-3) attains a terminal velocity of 10 cm S^-1 when falling in a tank of water (coefficient of viscosity) water = 8.5\(\times\)10^-4pa s. What will the terminal velocity in glycerine (P = 1.2 g cm^-3, η = 13.2 ρa.s) be?

Discuss the ideal gas laws.

Explain Wien’s law and why our eyes are sensitive only to visible rays?

Distinguish between conduction, convection and radiation.

What is meant by coefficient of linear expansion superficial & cubical expansion?

A football at 27°C has 0.5 mole of air molecules. Calculate the internal energy of air in the ball.

Calculate the rms speed, average speed and the most probable speed of 1 mole of hydrogen molecules at 300 K. Neglect the mass of electron.

Explain postulates of the kinetic theory of gases.

Motor volume is occupied 1 moleof any (ideal) gas at standard temperature and pressure. Show that it is 22.4 litres.

Consider a particle undergoing simple harmonic motion. The velocity of the particle at position x₁ is v₁ and velocity of the particle at position x₂ is v₂. Show that the ratio of time period and amplitude is 
\(\frac { T }{ A } =2\pi \sqrt { \frac { { x }_{ 2 }^{ 2 }-{ x }_{ 1 }^{ 2 } }{ { { v }_{ 1 }^{ 2 }x }_{ 2 }^{ 2 }-{ { v }_{ 2 }^{ 2 }x }_{ 1 }^{ 2 } } } \)

Discuss the simple pendulum in detail.

Explain briefly about oscillations.

The bob of simple pendulum executes S.H.M is water with a period t, while the period of oscillation of the bob is to in air, neglecting frictional force of water and given that the density of the bob is \(\frac{4000}{3}\)kg m^-3, find the relationship between t and t₀?

What is meant by Doppler effect?
Discuss the following cases
(1) Source in motion and Observer at rest
(a) Source moves towards observer
(b) Source moves away from the observer
(2) Observer in motion and Source at rest
(a) Observer moves towards Source
(b) Observer resides away from the Source
(3) Both are in motion
(a) Source and Observer approach each other
(b) Source and Observer resides from each other
(c) Source chases Observer
(d) Observer chases Source

Consider a mixture of 2 mol of helium and 4 mol of oxygen. Compute the speed of sound in this gas mixture at 300 K.

For the travelling : harmonic wave y(x, t) = 2.0 cos 2π [St - 0.0060x + 0.27], where x and yare in cm and t in s.
Calculate the phase difference between oscillatory motion of two points separated by a distance of,
(a) 300 cm
(b) 0.75 m (c)\(\lambda\over 4\)

A transverse harmonic wave on a string is described by y(x, t) = 5.0 sin (48t + 0.0264x + ), where x and y are in cm and t in sec. The positive direction of x is from left to right.
(a) What are its amplitude and frequency?
(b) What is the least distance between two success in crests in the wave?