Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem.
(i) 8,15,17
(ii) 12,13,15
(iii) 30, 40, 50
(iv) 9, 40, 41
(v) 24, 45, 51

Find the unknown side in the following triangles.
  

An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height.

In the figure, find PR and QR.

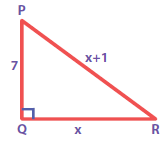
The length and breadth of the screen of an LED-TV are 24 inches and 18 inches. Find the length of its diagonal.

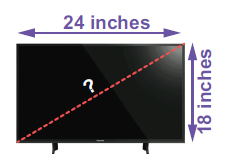
Find the distance between the helicopter and the ship.

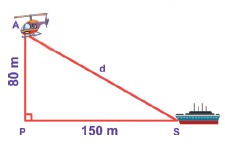
From the figure,
(i) If TA = 3cm and OT = 6cm, find TG.

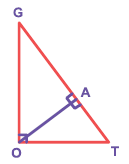
If RQ = 15 cm and RP = 20 cm, find PQ, PS and SQ.

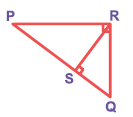
The sides of a triangle are 1.2 cm, 3.5 cm and 3.7 cm. Is this triangle a right triangle? If so, which side is the hypotenuse?

Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Why?

Find the length of the support cable required to support the tower with the floor.

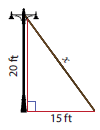
A ramp is constructed in a hospital as shown. Find the length of the ramp.

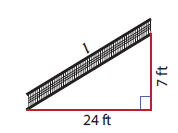
In the figure, find MT and AH.

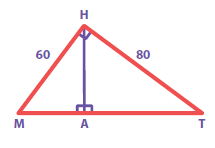
Mayan travelled 28 km due north and then 21 km due east. What is the least distance that he could have travelled from his starting point?

If ∆ APK is an isosceles right angled triangle, right angled at K. Prove that AP² = 2AK².

The diagonals of the rhombus is 12 cm and 16 cm. Find its perimeter. (Hint: the diagonals of rhombus bisect each other at right angles).

In the figure, find AR.

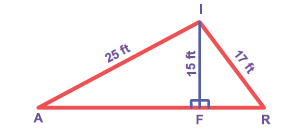
∆ ABC is a right angled triangle in which ㄥA = and AM ⊥ BC. Prove that AM = \(\frac { AB\times AC }{ BC } \). Also if AB = 30 cm and AC = 40 cm, find AM.

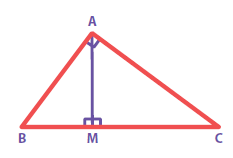
I. Construct the following trapeziums with the given measures and also find their area.
1. AIMS with \(\overset { \_ \_ }{ AI } \) || \(\overset { \_ \_ }{ SM } \), AI = 6 cm, IM = 5 cm, AM = 9 cm and MS = 6.5 cm.
2. CUTE with \(\overset { \_ \_ }{ CD } \) || \(\overset { \_ \_ }{ ET } \), CU = 7 cm, ㄥUCE = 80⁰ CE = 6 cm and TE = 5 cm..
3. ARMY with \(\overset { \_ \_ }{ AR } \) || \(\overset { \_ \_ }{ YM } \), AR = 7 cm, RM = 6.5 cm ㄥRAY = 100⁰ and ㄥARM = 60⁰
4. CITY with \(\overset { \_ \_ }{ CI } \) || \(\overset { \_ \_ }{ YT } \), CI = 7 cm, IT = 5.5 cm, TY = 4 cm and YC = 6 cm.

I. Construct the following parallelograms with the given measurements and find their area.
1. ARTS, AR = 6 cm, RT = 5 cm and ㄥART = 70⁰. .
2. CAMP, CA = 6 cm, AP = 8 cm and CP = 5.5 cm.
3. EARN, ER = 10 cm, AN = 7 cm and ㄥEOA = 110° where \(\overset { \_ \_ }{ ER } \) and \(\overset { \_ \_ }{ AN } \) intersect at O.
4. GAIN, GA = 7.5 cm, GI = 9 cm and ㄥGAI = 100⁰.