The rational number (numbers) which has (have) additive inverse is (are)

Multiplicative inverse of 0 (is)

\(\frac{1}{2}+\frac{6}{4}\) is 

\(\frac { 1 }{ 2 } \times \left( \frac { 2 }{ 3 } +\frac { 6 }{ 4 } \right) =\left( \frac { 1 }{ 2 } +\frac { 2 }{ 3 } \right) +\left( \frac { 1 }{ 2 } \times \_ \_ \right) \)

\(\frac { 1 }{ 2 } \times \left( \frac { 1 }{ 3 } +\frac { 1 }{ 4 } \right) =\left( \frac { 1 }{ 2 } +\frac { 1 }{ 3 } \right) +\frac { 1 }{ 4 } \)

In  if the faces shows the area in the net, then the shape mentioned is

If V = 6, E = 12 then the faces of the polyhedron is

Exact value of \(\pi\) is

If any two points on a circles is joined the line segment is called as

The line segment which connects any two faces are called ______.

The missing terms in the product - 3m3n x 9(_) = ___________m⁴n³ are

If the area of a square is 36x⁴y²t hen, its side is______

Volume of the rectangle 1 = 2ab, b = 3ac and h = 2ac is _________.

Product of 6a² - 7b + ab and 2ab is __________.

Square of (3x - 4y) is _______.

Two similar triangles will always have ________angles

If in triangles PQR and XYZ, \(\frac{PQ}{XY}=\frac{QR}{ZX}\) then they will be similar if

A flag pole 15 m high casts a shadow of 3 m at 10 a.m. The shadow cast by a building at the same time is 18.6 m. The height of the building is

If ΔABC～ΔPQR in which ∠A = 53^o and ∠Q = 77^o, then R is

In the figure, which of the following statements is true?

How many outcomes can you get when you toss three coins once?

In how many ways can you answer 3 multiple choice questions, with the choices A, B, C and D?

How many 2 digit numbers contain the number 7?

If 48% of  48 = 64% of x , then x =

A fruit vendor sells fruits for Rs. 200 gaining Rs. 40. His gain percentage is

A man buys an article for Rs.150 and makes overhead expenses which are 12% of the cost price. At what price must he sell it to gain 5%?

The number of conversion periods, if the interest on a principal is compounded every two months is___________.

The time taken for Rs.4400 to become Rs.4851 at 10%, compounded half yearly is _______.

The exterior angle of a triangle is 120° and one of its interior opposite angle 58°, then the other opposite interior angle is________.

The product of LCM and HCF of two numbers is 24. If one of the number is 6, then the other number is ________.

The hypotenuse of a right angled triangle of sides 12cm and 16cm is __________.

If the square of the hypotenuse of an isosceles right triangle is 50 cm², the length of each side is ____________.

The sides of a right angled triangle are in the ratio 5: 12: 13 and its perimeter is 120 units then, the sides are ______________.

Every 3rd number of the Fibonacci sequence is a multiple of _______

Every _______ number of the Fibonacci sequence is a multiple of 8

The difference between the 18^th and 17^th Fibonacci number is

There are four groups of letters in each set. Three of these sets are a like in some way while one is different. Find the one which is different.

Praveen recently got the registration number for his new two-wheeler. Here, the number is given in the form of mirror-image. Encode the image and find the correct registration number of praveen’s two-wheeler.

Write five rational numbers which are less than –2.

Mark the following rational numbers on a number line.
\(\frac{5}{-4}\)

Multiply \(\frac{3}{4}\) by \(\frac{5}{17}\)

Divide 1 by \(\frac{1}{2}\)

What should we multiply with \(\frac{-15}{28}\)to get \(\frac{-5}{7}?\)

Find the area of a sector whose length of the arc is 50 mm and radius is 14 mm.

Find the area of the combined figure given which is got by joining of two parallelograms

List out atleast three objects in each category which are in the shape of cube, cuboid, cylinder, cone and sphere.

Can a polyhedron have for its faces = 12 edges = 16 and vertices = 6.

Can a polyhedron have 10 faces, 20 edges and 15 vertices?

Identify the errors and correct them. (4n)² − 2n  +3 = 4n²− 2n + 3

3x²(x⁴ - 7x³+ 2) what is the highest power in the expression.

Evaluate:
(2x-3y)²

(7x - 5)² Expand

Factorize - xy - ay

In the figure, ∠TMA ≡ ∠IAM and ∠TAM ≡ ∠IMA . P is the midpoint of MI and N is the midpoint of AI. Prove that ΔPIN～ΔATM.

Fill in the blanks with the correct term from the given list.
(in proportion, similar, corresponding, congruent shape, area, equal)
(i) Corresponding sides of similar triangles are _______.
(ii) Similar triangles have the same _________ but not necessarily the same size.
(iii) In similar triangles, ______ sides are opposite to equal angles.
(iv) The symbol ≡ is used to represent _______ triangles.
(v) The symbol ～ is used to represent ________ triangles

Match the following by their congruence

S.No.	A		B
1.		(i)	RHS
2.		(ii)	SSS
3.		(iii)	SAS
4.		(iv)	ASA

Is it possible to construct a quadrilateral PQRS with PQ = 5 cm, QR = 3 cm, RS = 6 cm, PS = 7 cm and PR = 10 cm. If not, why?

In the given figure if \(\angle \)P =\(\angle \)RTS, prove that \(\triangle \)RPQ ~\(\triangle \) RTS.

Shanthi has 5 chudithar sets and 4 frocks. In how many possible ways, can she wear either a chudithar or a frock?

Convert the tree diagram into a numeric expression.

If the numerator of a fraction is increased by 50% and the denominator is decreased by 20%, then it becomes \(\frac { 3 }{ 5 } \). Find the original fraction.

A fruit vendor bought some mangoes of which 10% were rotten. He sold 33\(\frac { 1 }{ 3 } \) % of the rest. Find the total number of mangoes bought by him initially, if he still has 240 mangoes with him.

Use the graph to determine the coordinates where each figure is located
a) Star _______
b) Bird _______
c) Red Circle _______
d) Diamond _______
e) Triangle _______
f) Ant _______
g) Mango _______
h) Housefly _______
i) Medal _______
j) Spider _______

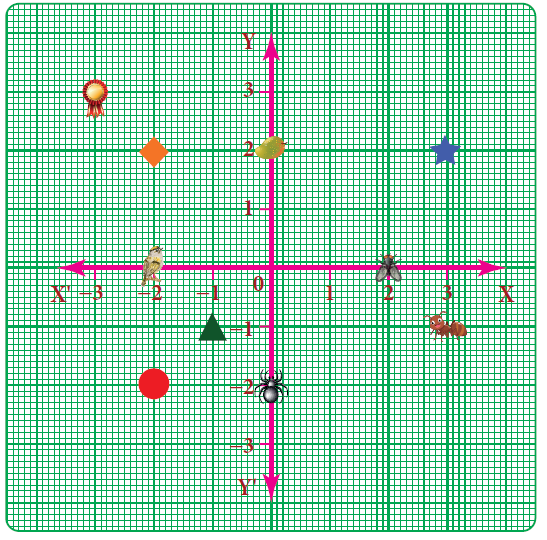
Draw the graph of the following equations
(i) x = −7 (ii) y = 6

In triangle ABC, the measure of ∠B is two-third of the measure of ∠A. The measure of ∠C is 20° more than the measure of ∠A. Find the measures of the three angles.

Find the unknown side in the following triangles.
  

Mayan travelled 28 km due north and then 21 km due east. What is the least distance that he could have travelled from his starting point?

In the figure, find AR.

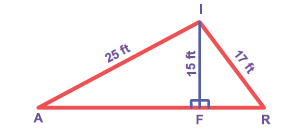
∆ ABC is a right angled triangle in which ㄥA = and AM ⊥ BC. Prove that AM = \(\frac { AB\times AC }{ BC } \). Also if AB = 30 cm and AC = 40 cm, find AM.

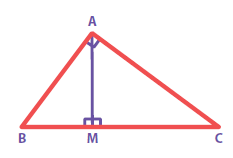
I. Construct the following trapeziums with the given measures and also find their area.
1. AIMS with \(\overset { \_ \_ }{ AI } \) || \(\overset { \_ \_ }{ SM } \), AI = 6 cm, IM = 5 cm, AM = 9 cm and MS = 6.5 cm.
2. CUTE with \(\overset { \_ \_ }{ CD } \) || \(\overset { \_ \_ }{ ET } \), CU = 7 cm, ㄥUCE = 80⁰ CE = 6 cm and TE = 5 cm..
3. ARMY with \(\overset { \_ \_ }{ AR } \) || \(\overset { \_ \_ }{ YM } \), AR = 7 cm, RM = 6.5 cm ㄥRAY = 100⁰ and ㄥARM = 60⁰
4. CITY with \(\overset { \_ \_ }{ CI } \) || \(\overset { \_ \_ }{ YT } \), CI = 7 cm, IT = 5.5 cm, TY = 4 cm and YC = 6 cm.

The rule of Fibonacci Sequence is F(n) = F(n–2) + F(n–1). Find the 11^th to 20^th Fibonacci numbers.

Find the length of the largest which piece of wood used to measure exactly the lengths 4m50cm and 6m 30cm woods.( Use repeated subtraction method)

Using both repeated division method and repeated subtraction method and find the greatest number that divides 167 and 95, leaving 5 as reminder

Write the following decimal numbers as rationals.
−5.8

Simplify \(\frac { 2 }{ 5 } +\frac { 8 }{ 3 } +\frac { -11 }{ 15 } +\frac { 4 }{ 5 } +\frac { -2 }{ 3 } \)

From the three vertices of an equilateral triangle of side 12 cm, Nishanth cuts sectors of 5 cm radius each and forms the following shape. Find the area of that shape. (π = 3.14)

Give the net pattern for a tetrahedron.

Expand (x + 4)³

Factorize
4a² - 4a + 1

(Illustrating SSS similarity)
Prove that ΔPQR ～ ΔPRS in the given Fig

Two triangles BAC and BDC right angled at A and D respectively are drawn on the same base BC and on the same side of BC. If AC and DB intersect at P. Prove that AP x PC = DP x PB.

Colour the graph with minimum number of colours and no two adjacent vertices should have the same colour.

When a number is decreased by 25% it becomes 120. Find the number.

Solve 2x + 5 = 9

Can a right triangle have sides that measure 5cm, 12cm and 13cm?

A 20- feet ladder leans against a wall at height of 16 feet from the ground. How far is the base of the ladder from the wall?

Use Ceasar Cipher table set + 4 and to try to solve the given secret sentence.
fvieo mr gshiw ger fi xvmgoc

Simplify \(\left( \frac { -7 }{ 18 } \times \frac { 15 }{ -7 } \right) -\left( 1\times \frac { 1 }{ 4 } \right) +\left( \frac { 1 }{ 2 } \times \frac { 1 }{ 4 } \right) \)

In the figure AOBCA represents a quadrant of a circle of radius 3.5cm D with center 'O' calculate the area of the shaded portion \(\left( \pi =\frac { 22 }{ 7 } \right) \)

Velu pastes ‘ 4xy ’ pictures in one page of his scrap book. How many pages will he need to paste 100x²y³pictures? (x, y are positive integers).

In the given figure if \(\frac { QT }{ PR } =\frac { QR }{ QS } \) and \(\angle \)1 = \(\angle \)2.Prove that \(\triangle \)PQS ~\(\triangle \)TQR.

Colour a map of South India in the given figure with the fewest number of colours.

The cost price of 16 boxes of strawberries is equal to the selling price of 20 boxes of strawberries. Find the gain or loss percentage.

The sum of the digits of a two-digit number is 8. If 18 is added to the value of the number, its digits get reversed. Find the number.

Construct a trapezium DEAN in which \(\overset { \_ \_ }{ DE } \) is parallel to \(\overset { \_ \_ }{ NA } \), DE = 7 cm, EA = 6.5 cm ㄥEDN = 100⁰ and ㄥDEA = 70⁰. Also find its area.

There are 270 ginger chocolates, 384 milk chocolates and 588 coconut chocolates. What is the largest number of containers possible so that each container contains the same number of chocolates of each kind?