- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

9th Standard Mathematics English Medium All Chapter Book Back and Creative Three Marks Questions 2020 Question Bank Software Mar-14 , 2020
9th Standard Mathematics English Medium All Chapter Book Back and Creative Three Marks Questions 2020
-
Draw: Venn diagram for each of the following:
(i) \(A\cup (B\cap C)\)
(ii) \(A\cap (B\cup C)\)
(iii) \((A\cup B)\cap C\)
(iv) \((A\cap B)\cup C\) -
If A = {-2,0,1,3,5}, B = {-1,0,2,5,6} and C = {-1,2,5,6,7} then show that A-(BUC) = (A-B)∩(A-C).
-
If A = {2,5,6,7} and B = {3,5,7,8}, then verify the commutative property of union sets
-
If A = {2,5,6,7} and B = {3,5,7,8}, then verify the commulative property of intersection of sets
-
Express the following decimal expression into rational numbers. 0.86
-
Can you reduce the following numbers to surds of same order :
(i) \(\sqrt{3}\)
(ii) \(\sqrt [ 4 ]{ 3 } \)
(iii) \(\sqrt [ 3 ]{ 3 } \) -
Compute and give the answer in the simplest form; \(3\sqrt { 162 } \times 7\sqrt { 50 } \times 6\sqrt { 98 } \)
-
Write in scientific notation : (0.00000004)3
-
Add the following polynomials and find the degree of the resultant polynomial.
p(x) = 6x2-7x+2 q(x) = 6x3-7x+15 -
Show that x+4 is a factor of x3 + 6x2 - 7x - 60
-
Find the GCD of ax, ax+y, ax+y+z
-
Check whether (5, −1) is a solution of the simultaneous equations x – 2y = 7 and 2x + 3y = 7.
-
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent:
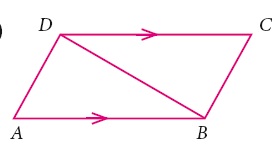
-
ABCD is a parallelogram and AP and CQ are perpendic from vertex A and C on diagonal BD. Show that
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
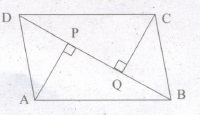
-
ABCD is a rectangle and P, Q, Rand S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
-
Draw the \(\triangle \)ABC , where AB = 6 cm, B = 110° and AC = 9 cm and construct the centroid.
-
Show that the following points taken in order form the vertices of a parallelogram.
A (–7, –3), B(5, 10), C(15, 8) and D(3, –5) -
Read the coordinates of the vertices of the triangle ABC with the following figure.
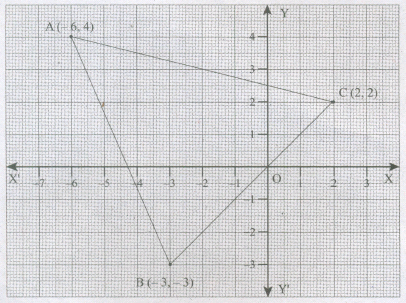
-
Three vertices of a rectangle are (3, 2), (-4, 2) and (-4, 5). Plot the points and find the coordinates of the fourth vertex.
-
Plot the following points on a graph sheet by taking the scale as 1cm = 1 unit.
Find how far the points are from each other?
A (1,0) and D (4, 0). Find AD and also DA.
Is AD = DA?
You plot another set of points and verify your Result.
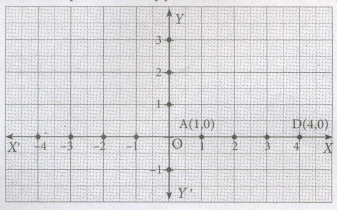
-
If the mean of the following data is 20.2, then find the value of p
Marks 10 15 20 25 30 No.of students 6 8 p 10 6 -
For the data 11,15,17, x+1,19, x-2, 3 if the mean is 14,find the value of x, Also find the mode of the data.
-
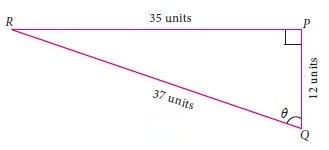
For the measures in the figure, compute sine, cosine and tangent ratios of the angle \(\theta \)
-
(i) If cosec A = sec 340, then find A
(ii) If tan B = cot 470, then find B. -
Find the Total Surface Area and Lateral Surface Area of the cube, whose side is 5 cm.
-
The total surface area of a cube is 864 cm2. Find its volume
-
When a dice is rolled, find the probability to get the number greater than 4?
-
In a recent year, of the 1184 centum scorers in various subjects in tenth standard public exams, 233 were in mathematics. 125 in social science and 106 in science. If one of the student is selected at random, find the probability of that selected student,
(i) is a centum scorer in Mathematics
(ii) is not a centum scorer in Science
Answer All The Following Question:
30 x 3 = 90






 9th Standard Maths Syllabus
9th Standard Maths Syllabus  9th Standard Maths Study Materials
9th Standard Maths Study Materials

Reviews & Comments about 9th Standard Mathematics English Medium All Chapter Book Back and Creative Three Marks Questions 2020
Write your Comment