If in triangles ABC and EDF,\(\cfrac { AB }{ DE } =\cfrac { BC }{ FD } \) then they will be similar, when

If in \(\triangle\)ABC, DE || BC, AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is

Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?

How many tangents can be drawn to the circle from an exterior point?

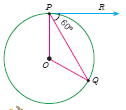
In figure if PR is tangent to the circle at P and O is the centre of the circle, then \(\angle PQR\) is

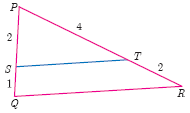
Show that \(\triangle\) PST~\(\triangle\) PQR 

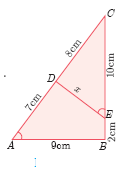
\(\angle A=\angle CED\) prove that \(\Delta\ CAB \sim \Delta CED\) Also find the value of x.

If \(\triangle\)ABC is similar to \(\triangle\)DEF such that BC = 3 cm, EF = 4 cm and area of \(\triangle\)ABC = 54 cm². Find the area of \(\triangle\)DEF.

Construct a triangle similar to a given triangle PQR with its sides equal to \(\frac { 7 }{ 4 } \) of the corresponding sides of the triangle PQR (scale factor \(\frac { 7 }{ 4 } \)>1)

An insect 8 m away initially from the foot of a lamp post which is 6 m tall, crawls towards it moving through a distance. If its distance from the top of the lamp post is equal to the distance it has moved, how far is the insect away from the foot of the lamp post?

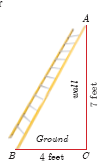
What length of ladder is needed to reach a height of 7 ft along the wall when the base of the ladder is 4 ft from the wall? Round off your answer to the next tenth place.

In figure the line segment XY is parallel to side AC of \(\Delta ABC\) and it divides the triangle into two parts of equal areas. Find the ratio \(\cfrac { AX }{ AB } \)

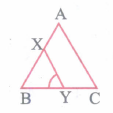
In \(\triangle\) ABC, if DE||BC, AD = x, DB = x − 2, AE = x +2 and EC = x − 1 then find the lengths of the sides AB and AC.

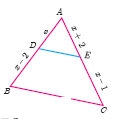
In the Figure, AD is the bisector of \(\angle\)BAC, if A = 10 cm, AC = 14 cm and BC = 6 cm. Find BD and DC.

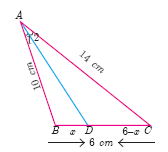
Find the length of the tangent drawn from a point whose distance from the centre of a circle is 5 cm and radius of the circle is 3 cm.

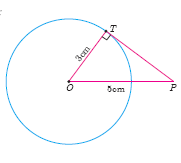
In trapezium ABCD, AB || DC, E and F are points on non-parallel sides AD and BC respectively, such that EF || AB. Show that \(\frac { AE }{ ED } =\frac { BF }{ FC } \)

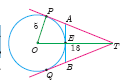
In figure, O is the centre of the circle with radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle E, if AB is the tangent to the circle at E, find the length of AB