- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Chemistry
-

Physics
-

Maths
-

Accountancy
-

Business Studies
-

Economics
-

Introductory Micro and Macroeconomics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Political Science
-

Engineering Graphics
-

Bio Technology
-

Entrepreneurship
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Psychology
-

Hindi Core
-

Tamil
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Physics
-

Mathematics
-

Chemistry
-

Biology
-

Economics
-

Business Studies
-

Accountancy
-

Computer Science
-

English
-

Geography
-

History
-

Physical Education
-

Psychology
-

Sociology
-

Bio Technology
-

Enterprenership
-

Hindi
-

Home Science
-

Political Science
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Social Science
-

Mathematics
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students
Revision Model Question Paper 2
11th Standard
-
Reg.No. :
Business Maths
Time :
03:00:00 Hrs
Total Marks :
90
-
The inventor of input-output analysis is ________.
(a)Sir Francis Galton
(b)Fisher
(c)Prof. Wassily W. Leontief
(d)Arthur Caylay
-
If \(\begin{vmatrix} x & 2 \\ 8 &5 \end{vmatrix}=0\) then the value of x is ________.
(a)\({{-5}\over{6}}\)
(b)\({{5}\over{6}}\)
(c)\({{-16}\over{5}}\)
(d)\({{16}\over{5}}\)
-
If nPr = 720 (nCr), then r is equal to ______.
(a)4
(b)5
(c)6
(d)7
-
The term containing x3 in the expansion of (x - 2y)7 is _________.
(a)3rd
(b)4th
(c)5th
(d)6th
-
The slope of the line 7x + 5y - 8 = 0 is _______.
(a)7/5
(b)-7/5
(c)5/7
(d)-9/7
-
Length of the latus rectum of the parabola y2 = - 25x is _______.
(a)25
(b)-5
(c)5
(d)-25
-
The value of sin 15o cos 15o is ______.
(a)1
(b)\(\frac{1}{2}\)
(c)\(\frac{\sqrt3}{2}\)
(d)\(\frac{1}{4}\)
-
If p sec 50o = tan 50o then p is _______.
(a)cos 50o
(b)sin 50o
(c)tan 50o
(d)sec 50o
-
The graph of f(x) = ex is identical to that of ________.
(a)f(x) = ax, a > 1
(b)f(x) = ax, a < 1
(c)f(x) = ax, 0 < a < 1
(d)y = ax +b, a \(\ne\) 0
-
\(\frac{d}{dx}(\frac{1}{x})\) is equal to ________.
(a)\(-\frac{1}{x^2}\)
(b)\(-\frac{1}{x}\)
(c)log x
(d)\(\frac{1}{x^2}\)
-
Marginal revenue of the demand function p = 20–3x is _______.
(a)20–6x
(b)20–3x
(c)20+6x
(d)20+3x
-
If demand and the cost function of a firm are p = 2–x and c = 2x2 + 2x + 7 then its profit function is ________.
(a)x2 + 7
(b)x2 - 7
(c)- x2 + 7
(d)- x2 - 7
-
A man purchases a stock of Rs. 20,000 of face value Rs. 100 at a premium of 20%, then investment is ________.
(a)Rs. 20,000
(b)Rs. 25,000
(c)Rs. 24,000
(d)Rs. 30,000
-
The % Income on 7 % stock at Rs. 80 is _______.
(a)9%
(b)8.75%
(c)8%
(d)7%
-
The geometric mean of two numbers 8 and 18 shall be _________.
(a)12
(b)13
(c)15
(d)11.08
-
If median = 45 and its coefficient is 0.25, then the mean deviation about median is _________.
(a)11.25
(b)180
(c)0.0056
(d)45
-
Correlation co-efficient lies between ______.
(a)0 to ∞
(b)-1 to +1
(c)-1 to 0
(d)-1 to ∞
-
The person suggested a mathematical method for measuring the magnitude of linear relationship between two variables say X and Y is ________.
(a)Karl Pearson
(b)Spearman
(c)Croxton and Cowden
(d)Ya Lun Chou
-
The critical path of the following network is________.
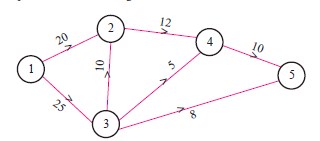 (a)
(a)1 – 2 – 4 – 5
(b)1 – 3 – 5
(c)1 – 2 – 3 – 5
(d)1 – 2 – 3 – 4 – 5
-
The minimum value of the objective function Z = x + 3y subject to the constraints 2x + y ≤ 20, x + 2y ≤ 20, x > 0 and y > 0 is ______.
(a)10
(b)20
(c)0
(d)5
-
Evaluate: \(\left| \begin{matrix} 1 & 2 & 4 \\ -1 & 3 & 0 \\ 4 & 1 & 0 \end{matrix} \right| \)
-
ResoIve into partial fractions :\(\frac { 12x-17 }{ (x-2)(x-1) } \)
-
A point in the plane moves so that its distance from the origin is thrice its distance from the y- axis. Find its locus.
-
If \(\tan^2x=2\tan^2\phi+1\), prove that \(\cos2x+sin^2\phi=0\)
-
For what value of k, the following function is continous at x =0?
f(x) = \(\begin{cases} \frac { 1-cos4x }{ 8{ x }^{ 2 } } \quad ifx\neq 0 \\ k\quad \quad \quad ifx=0 \end{cases}\) -
The demand function for a commodity is \(p={4\over x}\), where p is unit price. Find the instantaneous rate of change of demand with respect to price at p = 4. Also interpret your result.
-
Find the amount of annuity of Rs. 2000 payable at the end of each year for 4 years of money is worth 10% compounded annually [(1.1)4 = 1.4641]
-
From a pack of 52 cards, two cards are drawn at random. Find the probability that one is a king and the other is a queen.
-
From the following data calculate the correlation coefficient Σxy = 120, Σx2 = 90, Σy2 = 640
-
Develop a network based on the following information:
Activity: A B C D E F G H Immediate predecessor: - - A B C, D C, D E F -
Prove that \(\left| \begin{matrix} x & sin\theta & cos\theta \\ -sin\theta & -x & 1 \\ cos\theta & 1 & x \end{matrix} \right| \) is independent of \(\theta\)
-
If \(A=\left[ \begin{matrix} 2 & 4 \\ -3 & 2 \end{matrix} \right] \)then, find A -1.
-
Find x if \(\frac { 1 }{ 6! } +\frac { 1 }{ 7! } =\frac { x }{ 8! } \).
-
Find the equation of the parabola whose focus is the point F(-1, -2) and the directrix is the line 4x - 3y + 2 = 0
-
Differentiate the following with respect to x. \(\sqrt { 1+{ x }^{ 2 } } \)
-
Find the equilibrium price and equilibrium quantity for the following functions. Demand: x = 100 – 2p and supply: x = 3p – 50
-
Which is better investment? 7% of Rs. 100 shares at Rs. 120 (or) 8% of Rs. 100 shares at Rs. 135.
-
Find Q2 for 37, 32, 45, 36, 39, 37, 46, 57, 27, 34, 28, 30, 21
-
Find the regression co-efficient of x on y from the following data. \(\sum\)X=20, \(\sum\)Y=40, \(\sum\)XY=300, \(\sum\)X2=150, \(\sum\)Y2=345, N=5. Find the value of x when y=5
-
Construct a network diagram for the following situation:
A < D, E; B, D < F; C < G and B < H. -
-
Three coins are tossed simultaneously. Consider the events A ‘three heads or three tails’, B ‘atleast two heads’ and C ‘at most two heads’ of the pairs (A, B), (A, C) and (B, C), which are independent? Which are dependent?
-
Solve the following linear programming problem graphically.
Maximise Z = 4x1 + x2 subject to the constraints x1 + x2 ≤ 50; 3x1 + x2 ≤ 90 and x1 ≥ 0, x2 ≥ 0.
-
-
-
Prove that : cos20°cos40°cos80° = \(\frac { 1 }{ 8 } \)
-
A man sells 2000 ordinary shares (par value Rs. 10) of a tea company which pays a dividend of 25% at Rs. 33 per share. He invests the proceeds in cotton textiles (par value Rs. 25) ordinary shares at 44 per share which pays a dividend of 15%. Find
(i) the number of cotton textiles shares purchased and
(ii) change in his dividend income.
-
-
-
An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How side is 2 m from the vertex of the parabola?
-
For the total revenue function R = - 90 + 6x2 - x3 find when R is increasing and when it is decreasing. Also, discuss the behaviour of marginal revenue.
-
-
-
The demand for a commodity A is q = 80 - \({ p }_{ 1 }^{ 2}\) + 5p2 - p1p2. Find the partial elasticities \(\frac { { E }q }{ { E }p_{ 1 } } \) and \(\frac { { E }q }{ { E }p_{ 2 } } \) when p1 = 2, p2 = 1.
-
A computer while calculating the correlation co-efficient between two variables x and y from 25 pairs of observations, obtained the following results. \(\sum\)x=125, \(\sum\)x2=650, \(\sum\)y=100, \(\sum\)y2=460, xy=508. It was later found out that it had copied down two pairs as while the correct values are
x y 6 14 8 6 x y 8 12 6 8 Obtain the correlation co-efficient for the correct value.
-
-
-
Show that the middle term in the expansion of (1 + x)2n is \(\frac { 1.3.5....(2n-1){ 2 }^{ n }.{ x }^{ n } }{ n! } \)
-
Verify the continuity and differentiability of \(f(x)= \begin{cases}1-x & \text { if } x<1 \\ (1-x)(2-x) & \text { if } 1 \leq x \leq 2 \\ 3-x & \text { if } x>2\end{cases}\) at x = 1 and x = 2
-
-
-
Two types of radio values A, B are available and two types of radios P and Q are assembled in a small factory. The factory uses 2 valves of type A and 3 valves of type B for the type B for the type of radio P, and for the radio Q it uses 3 valves of type A and 4 valves of type B. If the number of valves of type A and B used by the factory are 130 and 180 respectively, find out the number of radios assembled use matrix method.
-
If the function \(f\left( x \right) =\begin{cases} 6ax+3b\quad if\quad x>1 \\ ax-2b\quad if\quad x<1\quad is\quad continuous\quad at\quad x=1 \\ 15\quad if\quad x=1 \end{cases}\) Find the value of a and b.
-
-
-
As the number of units manufactured increases from 6000 to 8000, the total cost of production increases from Rs. 33,000 to Rs. 40,000. Find the relationship between the cost (y) and the number of units made (x) if the relationship is linear.
-
Prove that the tangents to the circle x2 + y2 = 169 at (5,12) and (12,-5) are perpendicular to each other.
-
Part I
Answer all the questions.
Choose the most suitable answer
from the given four alternatives and write the option code with the
corresponding answer.
20 x 1 = 20
Part II
Answer any 7 questions. Question no. 30 is compulsory.
7 x 2 = 14
Part III
Answer any 7 questions. Question no. 40 is compulsory.
7 x 3 = 21
Part IV
Answer all the questions.
7 x 5 = 35
*****************************************
11th Standard Business Maths and Statistics Videos
TN 11th Maths Basic Algebra 50 Important 1 Marks Questions With Answers Book Back and Creative
TN Class 11 Maths Basic Algebra Study Materials TN State Board Samacheer / Matriculation 11th Maths Subject - Basic Algebra One Mark Question and Answers






 11th Standard Business Maths and Statistics Syllabus
11th Standard Business Maths and Statistics Syllabus  11th Standard Business Maths and Statistics Study Materials
11th Standard Business Maths and Statistics Study Materials 11th Standard Business Maths and Statistics MCQ Practise Tests
11th Standard Business Maths and Statistics MCQ Practise Tests 

Reviews & Comments about 11th Business Maths - Revision Model Question Paper 2
Write your Comment