The function f:[0,2π]➝[-1,1] defined by f(x) = sin x is

(a)

one-to-one

(b)

on to

(c)

bijection

(d)

cannot be defined

Let f:R➝R be defined by f(x) = 1 - |x|. Then the range of f is

(a)

R

(b)

(1,∞)

(c)

(-1,∞)

(d)

(-∞,1]

The shaded region in the adjoining diagram represents.

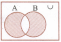(a)

A\B

(b)

B\A

(c)

AΔB

(d)

A'

Let R be the set of all real numbers. Consider the following subsets of the plane R x R: S = {(x, y) : y =x + 1 and 0 < x < 2} and T = {(x,y) : x - y is an integer} Then which of the following is true?

(a)

T is an equivalence relation but S is not an equivalence relation

(b)

Neither S nor T is an equivalence relation

(c)

Both S and T are equivalence relation

(d)

S is an equivalence relation but T is not an equivalence relation.

If f : R➝R is given by f(x) = 3x - 5, then f^-1(x) is __________

(a)

\(\frac{1}{3x-5}\)

(b)

\(\frac{x+5}{3}\)

(c)

does not exist since f is not one-one

(d)

does not exists since f is not onto

Let R be the universal relation on a set X with more than one element. Then R is

(a)

not reflexive

(b)

not symmetric

(c)

transitive

(d)

none of the above

\(n(p(A))=512,n(p(B))=32,n(A\cup B)=16,\) find \(n(A\cap B) \)  ___________

(a)

2

(b)

9

(c)

4

(d)

5

The range of the function is \(f(x)=\sqrt{3x^2-4x+5}\) is ___________

(a)

\(\left( -\infty,\sqrt{11\over 3}\right)\)

(b)

\(\left( -\infty,-\sqrt{11\over 3}\right)\)

(c)

\(\left( \sqrt{11\over 3},-\infty\right)\)

(d)

none

If A and B are any two finite sets having m and n elements respectively then the cardinality of the power set of A \(\times\) B is ___________

(a)

2^m

(b)

2ⁿ

(c)

mn

(d)

2^mn

The domain and range of the function \(f(x)={|x-4|\over x-4}\)

(a)

R, [-1, 1]

(b)

R \ {4};{-1,1}

(c)

R \ {4};{-1,l}

(d)

R, (-1,1)

Write the following in roster form.
\(\left\{ x:\frac { x-4 }{ x+2 } =3,x\in R-\{ -2\} \right\} \)

Let A and B be two sets such that n(A) = 3 and n(B) = 2. If (x, 1) (y, 2) (z, 1) are in A\(\times\)B, find A and B, where x, y, z are distinct elements.

If U = {x : 1 ≤ x ≤ 10, x ∈ N}, A = {1, 3, 5, 7, 9} and B = {2, 3, 5, 9, 10} then find A'UB'.

Let A={1,2,3,4} and B = {a,b,c,d}. Give a function from A\(\rightarrow\)B for each of the following:
neither one- to -one and nor onto.

Write the steps to obtain the graph of the function y = 3(x-1)²+5 from the graph y = x²

Show that the function f : R ⟶ R given by f(x) = cos x for all x ∈ R is neither one-one nor onto.

If A = {x : x = 3n, n ∈ Z} and B = {x : x = 4n, n ∈ Z} then find A ∩ B.

Check the relation R = {(1, 1) (2, 2) (3, 3),....,(n, n)} defined on the set S = {1, 2, 3, .. n} for the three basic relations.

See the figure below, here letters of the English alphabets are mapped onto.

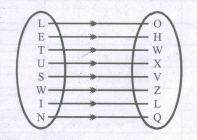
For the given curve y = x³ given in figure draw, try to draw with the same scale
(i) y = -x³ 
(ii) y = x³+1
(iii) y = x³-1
(iv) y = (x + 1)³

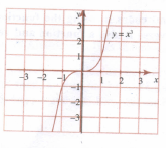
Show that the relation R defined on the set A of all polygons as R = {(P₁ P₂) : P₁ and P₂ have same number of sides} is an equivalence relation.

Let f: R ⟶ R be the signum function defined as \(f(x)=\begin{cases} 1,\ x>0\\0, x=0 \\-1, x<0 \end{cases}\)and g: R ⟶ R to the greatest integer function given by g(x) = [x]. Then prove that fog and gof coincide in [-1,0).