- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Chemistry
-

Physics
-

Maths
-

Accountancy
-

Business Studies
-

Economics
-

Introductory Micro and Macroeconomics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Political Science
-

Engineering Graphics
-

Bio Technology
-

Entrepreneurship
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Psychology
-

Hindi Core
-

Tamil
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Physics
-

Mathematics
-

Chemistry
-

Biology
-

Economics
-

Business Studies
-

Accountancy
-

Computer Science
-

English
-

Geography
-

History
-

Physical Education
-

Psychology
-

Sociology
-

Bio Technology
-

Enterprenership
-

Hindi
-

Home Science
-

Political Science
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Social Science
-

Mathematics
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

9th Mathematics Science All Chapter Annual Questions-I-2019-2020 Question Bank Software Feb-11 , 2020
9th Mathematics Science All Chapter Annual Questions-I-2019-2020
-
If n(A \(\cup \) B \(\cup \) C) = 40, n(A) = 30, n(B) = 25, n(C) = 20, n(A\(\cap \)B) = 12, n(B\(\cap \)C) = 18 and n(A\(\cap \)C) = 15 , then n(A\(\cap \)B\(\cap \)C) is ___________
(a)5
(b)10
(c)15
(d)20
-
In a town 30% like only coffee, 20% like only tea,10% like only like,15% like only any two of them, 5% only like all the three. What is the percentage of people who like none them.
(a)15%
(b)20%
(c)10%
(d)5%
-
The length and breadth of a rectangular plot are 5 \(\times\) 105 and 4 \(\times\) 104 metres respectively. Its area is ______.
(a)9 \(\times\) 101 m2
(b)9 \(\times\) 109 m2
(c)2 \(\times\) 1010 m2
(d)20 \(\times\) 1020 m2
-
In simple form,\(\sqrt [ 3 ]{ 54 } \) is ?
(a)\(3\sqrt [ 3 ]{ 2 } \)
(b)\(3\sqrt { 27 } \)
(c)\(3\sqrt { 2 } \)
(d)\(\sqrt { 3 } \)
-
x3 – x2 is a …………..
(a)monomial
(b)binomial
(c)trinomial
(d)constant polynomial
-
Degree of the linear polynomial is ________
(a)1
(b)2
(c)3
(d)4
-
The point of concurrency of the medians of a triangle is known as __________
(a)circumcentre
(b)incentre
(c)orthocentre
(d)centroid
-
The centre of a circle is (0, 0). One end point of a diameter is (5, -1), then ______________
(a)\(\sqrt{24}\)
(b)\(\sqrt{37}\)
(c)\(\sqrt{26}\)
(d)\(\sqrt{17}\)
-
The centroid of the triangle with vertices (−1, −6), (−2, 12) and (9, 3) is
(a)(3, 2)
(b)(2, 3)
(c)(4, 3)
(d)(3, 4)
-
The mean of the first 10 prime numbers is ___________
(a)12.6
(b)12.7
(c)12.8
(d)12.9
-
The mean of 5, 9, x, 17,and 21 is 13 then find the value of x ___________
(a)9
(b)13
(c)17
(d)21
-
if sin 300 = x and cos 600 = y, then x2 + y2 is________.
(a)\(\frac { 1 }{ 2 } \)
(b)0
(c)sin90°
(d)cos90°
-
If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is _______.
(a)3 cm2
(b)6 cm2
(c)9 cm2
(d)12 cm2
-
The six faces of the dice are called equally likely if the dice is _______.
(a)Small
(b)Fair
(c)Six-faced
(d)Round
-
Write down the power set of the following sets.
A = {a, b} -
Find the value of \({ 729 }^{ \frac { -5 }{ 6 } }\)
-
Convert the following rational numbers into decimal
(i) \(2\over 3\)
(ii) \(47\over 99\)
(iii) \(-{16\over 45}\) -
Find any 3 irrational numbers between 0.12 and 0.13.
-
Determine whether (x -1) is a factor of the following polynomials: x3+5x2-10x+4
-
Identify which ones are trapeziums and which are not.

-
Plot the points A( -1, 0), B( 3, 0), C(3, 4), and 0(-1, 4) on a graph sheet. Join them to form a rectangle. Draw the mirror image Of the diagram in clockwise direction:
(i) about x-axis.
(ii) about y-axis.
What is your observation on the coordinates of the mirror image? -
If A (10, 11) and B (2 ,3) are the coordinates of end points of diameter of circle. Then find the centre of the circle.
-
Find the centroid of the triangle whose vertices are (2, -5), (5, 11) and (9, 9)
-
A set of numbers consists of five 4’s, four 5’s, nine 6’s,and six 9’s. What is the mode.
-
Given that \(sin\alpha =\cfrac { 1 }{ \sqrt { 2 } } \) and \(tan\beta =\sqrt { 3 } \) Find the value of \(\alpha +\beta \)
-
Find the value of \(\cfrac { cos{ 63 }^{ 0 }20' }{ sin{ 26 }^{ 0 }40' } \)
-
The outer dimensions of a closed wooden box are 10 cm by 8 cm by 7 cm, Thickness of the wood is 1 cm3. Find the total cost of wood required to make box if 1 cm3 of wood costs Rs. 2.00?
-
In a football match, a goalkeeper of a team can stop the goal, 32 times out of 40 attempts tried by a team. Find the probability that the opponent team can convert the attempt into a goal.
-
In a class there are 40 students. 26 have opted for Mathematics and 24 have opted for Science. How many student have opted for Mathematics and Science.
-
If U = {x: −4 ≤ x ≤ 4, x \(\in \)Z}, A = {x :−4 < x ≤ 2, x\(\in \)Z } and B = {x :−2 ≤ x ≤ 3,x \(\in \) Z} , then verify De Morgan’s laws for complementation.
-
Express the following decimal expression into rational numbers -5.132
-
If \(\sqrt{2}\) =1.414, \(\sqrt{3}\) = 1.732, \(\sqrt{5}\) = 2.236, \(\sqrt{10}\) = 3.162 then find the values of the following correct to 3 places of decimals.
(i) \(\sqrt { 40 } -\sqrt { 20 } \)
(ii) \(\sqrt { 300 } -\sqrt { 90 } -\sqrt { 8 } \) -
Add \(\sqrt [ 5 ]{ 11 } \) and \(\sqrt [ 7 ]{ 11 } \). Check whether the sum is rational or irrational
-
Study the following pattern and write the algebraic expression
(i)
Shape Number 1 2 3 4 5 Number of matchsticks 4 7 10 13 16 (ii)
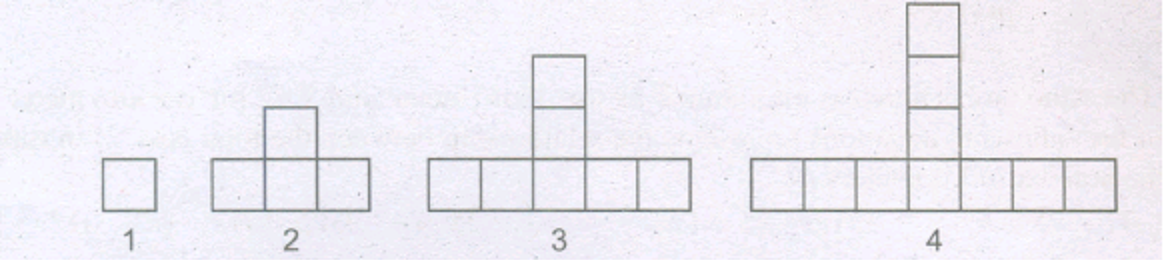
Shape Number 1 2 3 4 5 Number of Square Boxes 1 4 7 10 13 -
Show that (x-3) is a factor of x3 + 9x2 - x - 105
-
Draw the \(\triangle \)ABC , where AB = 6 cm, B = 110° and AC = 9 cm and construct the centroid.
-
The point (x, y) is equidistant from the points (3, 4) and (–5, 6). Find a relation between x and y.
-
Join the points taken in order and name the figure obtained. Name atleast any one point which is lying :
(i)On x-axis
(ii)On y-axis
(iii) In each of the Quadrants.
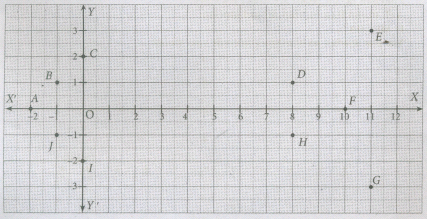
-
A researcher studying the behaviour of mice has recorded the time (in seconds) taken by each mouse to locate its food by considering 13 different mice as 31, 33, 63, 33, 28, 29, 33, 27, 27, 34, 35, 28, 32.Find the median time that mice spent in searching its food.
-
Express
(i) sin 74° in terms of cosine
(ii) tan 12° in terms of cotangent
(iii) cosec 39° in terms of secant -
Find the TSA and LSA of a cuboid whose length, breadth and height are 7.5 m, 3 m and 5 m respectively.
-
The probability that it will rain tomorrow is \(\\ \frac { 91 }{ 100 } \). What is the probability that it will not rain tomorrow?
-
Find the quotient and remainder when 5x3 + 7x2 + 3x + 2 is divided by 3x + 2
-
Solve by the method of elimination
(i) 2x–y = 3; 3x + y = 7
(ii) x–y = 5; 3x + 2y = 25
(iii) \(\frac { x }{ 10 } +\frac { y }{ 5 } =14;\frac { x }{ 8 } +\frac { y }{ 6 } =15\)
(iv) 3(2x + y) =7xy; 3(x + 3y) = 11xy
(v) \(\frac { 4 }{ x } +5y=7;\frac { 3 }{ x } +4y=5\)
(vi) 13x +11y = 70; 11x +13y = 74 -
In the given Fig. if AB = 2, BC = 6, AE = 6, BF = 8, CE = 7, and CF = 7, compute the ratio of the area of quadrilateral ABDE to the area of ΔCDF(Use congruent property of triangles).
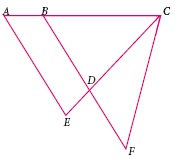
-
Draw and locate the centroid of the triangle ABC where right angle at A, AB = 8 cm and AC = 6 cm.
Part I
Answer all the questions.
Choose the most suitable answer from the given four alternatives and write the option code with the corresponding answer.
14 x 1 = 14
Part II
Answer any 10 questions. Question no. 28 is compulsory.
14 x 2 = 28
Part III
Answer any 10 questions. Question no. 42 is compulsory.
14 x 3 = 42
Part IV
Answer all the questions
4 x 5 = 20






 9th Standard Maths Syllabus
9th Standard Maths Syllabus  9th Standard Maths Study Materials
9th Standard Maths Study Materials

Reviews & Comments about 9th Mathematics Science All Chapter Annual Questions-I-2019-2020
Write your Comment