Which of the following is correct?

(a)

{7} ∈ {1,2,3,4,5,6,7,8,9,10}

(b)

7 ∈ {1,2,3,4,5,6,7,8,9,10}

(c)

7 ∉ {1,2,3,4,5,6,7,8,9,10}

(d)

{7} \(\nsubseteq \) {1,2,3,4,5,6,7,8,9,10}

A = {set of odd natural numbers}, B = {set of even natural numbers}, then A and B are ___________

(a)

equal set

(b)

equivalent sets

(c)

overlapping sets

(d)

disjoint sets

Sets having the same number of elements are called ___________

(a)

overlapping sets

(b)

disjoints sets

(c)

equivalent sets

(d)

equal sets

The number of elements of the set {x : x ∈ Z, x² = I} is ________

(a)

0

(b)

1

(c)

2

(d)

3

For any three sets A, B and C, (A−B)∩(B −C) is equal to ________.

(a)

A only

(b)

B only

(c)

C only

(d)

ф

The number \(0.\bar { 3 } \) in the form \(\frac { p }{ q } \) where p and q are integers and \(q\neq 0\)

(a)

\(\frac { 33 }{ 100 } \)

(b)

\(\frac { 3 }{ 10 } \)

(c)

\(\frac { 1 }{ 3 } \)

(d)

\(\frac { 3 }{ 100 } \)

Which of the following are irrational numbers?
\(\sqrt { 2+\sqrt { 3 } } \)
\(\sqrt [ 3 ]{ 5+\sqrt { 7 } } \)
\(\sqrt { 8-\sqrt [ 3 ]{ 8 } } \)
\(\sqrt { 4+\sqrt { 25 } } \)

(a)

(ii), (iii) and (iv)

(b)

(i), (ii) and (iv)

(c)

(i), (ii) and (iii)

(d)

(i), (iii) and (iv)

\(\sqrt{27}\)+\(\sqrt{12}\) = ________.

(a)

\(\sqrt{39}\)

(b)

5\(\sqrt{6}\)

(c)

5\(\sqrt{3}\)

(d)

3\(\sqrt{5}\)

Which of the following is not an irrational number?

(a)

\(\sqrt { 2 } \)

(b)

\(\sqrt { 5 } \)

(c)

\(\sqrt { 3 } \)

(d)

\(\sqrt { 25 } \)

\(\cfrac { \sqrt [ 3 ]{ 27 } }{ \sqrt [ 5 ]{ 3 } } \) is equal to_______

(a)

\(5\sqrt { 9 } \)

(b)

\(5\sqrt { 6 } \)

(c)

\(5\sqrt { 24 } \)

(d)

\(\sqrt [ 5 ]{ 30 } \)

The zero of the polynomial 2x+5 is _______.

(a)

\(\frac {5}{2}\)

(b)

\(-\frac {5}{2}\)

(c)

\(\frac {2}{5}\)

(d)

\(-\frac {2}{5}\)

Which of the following is trinomial?

(a)

-7z

(b)

\({ z }^{ 2 }-{ 4y }^{ 2 }\)

(c)

\({ x }^{ 2 }y-{ xy }^{ 2 }+y\)

(d)

\(12a=9ab+5b-3\)

The roots of the polynominal equation \({ x }^{ 2 }+2x=0\) are_______________

(a)

x = 0, 2

(b)

x = 1, 2

(c)

x = 1, -2

(d)

x = 0, -2

The degree of the polynomial \( \sqrt { 2 } { x }^{ 2 }-\frac { 7 }{ 2 } { x }^{ 4 }+x-5x^{ 3 }\) is _______________ 

(a)

2

(b)

3

(c)

4

(d)

5

If x - 3 is a factor of p(x), then the remainder is _______.

(a)

3

(b)

-3

(c)

p(3)

(d)

p(-3)

Which of the following has a factor?

(a)

x² + 2x

(b)

(x - 1)²

(c)

(x + 1)²

(d)

(x² - 2²)

If all the four sides of a parallelogram are equal and the adjacent angles are of 120° and 60°, then the name of the quadrilateral is ______

(a)

rectangle

(b)

square

(c)

rhombus

(d)

kite

Diagonal of which of the following quadrilaterals do not bisect it into two congruent triangles?

(a)

rhombus

(b)

trapezium

(c)

square

(d)

rectangle

ABCD is a parallelogram as shown. Find x and y.

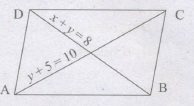(a)

1, 7

(b)

2, 6

(c)

3, 5

(d)

4, 4

In the figure, O is the centre of the circle and ㄥACB = 40° then ㄥAOB = ________.

(a)

80°

(b)

85°

(c)

70°

(d)

65°

In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ㄥQRS = 100°, then ㄥTVS = ______.

(a)

80°

(b)

100°

(c)

70°

(d)

90°

In the figure, PQRS and PTVS are two cyclic quadrilaterals, If  \(\angle\)QRS = 70°, then \(\angle\)TVS= __________

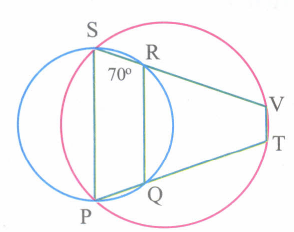(a)

70°

(b)

110°

(c)

80°

(d)

90°

The points (–5, 2) and (2, –5) lie in the ________.

(a)

same quadrant

(b)

II and III quadrant respectively

(c)

II and IV quadrant respectively

(d)

IV and II quadrant respectively

The distance between the point ( 5, –1 ) and the origin is _______.

(a)

\(\sqrt { 24 } \)

(b)

\(\sqrt { 37 } \)

(c)

\(\sqrt { 26 } \)

(d)

\(\sqrt { 17 } \)

On which quadrant does the point (- 4, 3) lie?

(a)

I

(b)

II

(c)

III

(d)

IV

A point which lies in the III quadrant is__________________

(a)

(5, 4)

(b)

(5, - 4)

(c)

(-5, - 4)

(d)

(-5,4)

The distance between the points (a, 0) and (0, b) is____________

(a)

a unit

 

(b)

b unit

(c)

\(\sqrt{a^2+{b^2}}\ unit\)

(d)

\(\sqrt{a^2-{b^2}}\ unit\)

The point which is on y-axis with ordinate - 5 is _____________

(a)

(0, - 5)

(b)

(-5,0)

(c)

(5,0)

(d)

(0,5)

The median of the first 10 whole numbers is ______________

(a)

4

(b)

4.5

(c)

5

(d)

5.5

The mean of a set of numbers is \(\bar X\). If each number is multiplied by z, the mean is _______.

(a)

\(\bar X + z\)

(b)

\(\bar X-z\)

(c)

z\(\bar X\)

(d)

\(\bar X\)

Which one of the following is not a measure of central tendency?

(a)

Mean

(b)

Range

(c)

Median

(d)

Mode

The mean of set of seven number is 81. If one of the nimbers is discarded,the mean of remaining number is 78. The value of discarded number is

(a)

101

(b)

100

(c)

99

(d)

98

A particular observation which occurs maximum number of times in a given data is called is

(a)

Frequency

(b)

range

(c)

mode

(d)

median

The mean of the first 10 whole number is

(a)

4

(b)

4.5

(c)

5

(d)

5.5

If tan \(\theta\) cot 37⁰ , then the value of \(\theta\) is ________.

(a)

37⁰

(b)

53⁰

(c)

90⁰

(d)

1⁰

If cos A = \(\frac { 3 }{ 5 } \), them the value of tan A is

(a)

\(\frac { 4 }{ 5 } \)

(b)

\(\frac { 3 }{ 4 } \)

(c)

\(\frac { 5 }{ 3 } \)

(d)

\(\frac { 4 }{ 3 } \)

The perimeter of an equilateral triangle is 30 cm. The area is _______.

(a)

\(10\sqrt { 3 } \) cm²

(b)

\(12\sqrt { 3 } \) cm²

(c)

\(15\sqrt { 3 } \) cm²

(d)

\(25\sqrt { 3 } \) cm ²

If the lateral surface area of a cube is 600 cm², then the total surface area is _______.

(a)

150 cm²

(b)

400 cm²

(c)

900 cm²

(d)

1350 cm²

A collection of one or more outcomes of an experiment is called _______.

(a)

Event

(b)

Outcome

(c)

Sample point

(d)

None of the above

The six faces of the dice are called equally likely if the dice is _______.

(a)

Small

(b)

Fair

(c)

Six-faced

(d)

Round

Which of the following are sets?
The Collection of rich people in India

Represent the following sets in set builder form.
E = The set of odd Whole numbers less than 9.

In a class of 50 students, each of the students passed either in mathematics or in science or in both. 10 students passed in both and 28 passed in science. Find how many students passed in mathematics only

Represent U= {1,2,3,4,5,6,7,8,9,10} A = {1,2,4,6,8,10} and B = {3,6,1,10} in venn-diagram, then find
(i) (A UB)'
(ii) (A ∩ B)'

Express the following in the form of \(\frac { p }{ q } \)  where p and q are integers and q \(\neq \)0.
(a)\(\overline { 0.6 } \) 
(b) \(\overline { 0.47 } \)
(c) \(\overline { 0.001 } \)

Evaluate: (0.1)^-4

Express the following in the form 3ⁿ: 27

Which arrow best shows the position of \(\frac { 11 }{ 3 } \) on the number line?

By remainder theorem, find the remainder when, p(x) is divided by g(x) where
p(x) = x³- 3x²+ 4x + 50 g(x) = x - 3

Expand: (2a + 3b)³

Solve \(\cfrac { 1 }{ 3 } x-\cfrac { 5 }{ 2 } =6\)

Identify which ones are trapeziums and which are not.

Draw ΔABC given AB = 9 cm, ㄥCAB = 115° and ΔABC = 40°. Locate its incentre and also draw the incircle. (Note: You can check from the above examples that the incentre of any triangle is always in its interior).

In a circle, AB and CD are two parallel chords with centre 0 and radius 5 em such that AB = 8 cm and CD = 6 cm determine the distance between the chords?

Find the value of X^o

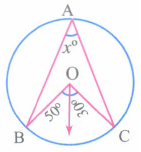
Plot the following points in the coordinate plane. Join them in order. What type of geometrical shape is formed? 
(–3, 3) (2, 3) (–6, –1) (5, –1)

If A (10, 11) and B (2 ,3) are the coordinates of end points of diameter of circle. Then find the centre of the circle.

In a rice mill, seven labours are receiving the daily wages of Rs. 500, Rs. 600, Rs. 600, Rs. 800, Rs. 800, Rs. 800 and Rs. 1000, find the modal wage

In a research laboratory scientists treated 6 mice with lung cancer using medicine. Ten days, they measured the volume of the tumor of the tumor in each mouse given the results in the table

Mouse marking	1	2	3	4	5	6
Tumor Volume(mm)3	145	148	142	141	139	140

Find the mean

If sin \(\theta\)  = \(\frac { a }{ \sqrt { { a }^{ 2 }+{ b }^{ 2 } } } \) then show that b sin \(\theta\) = a cos \(\theta\)

From the given figure, find all the trigonometric ratios of angle \(\theta\).

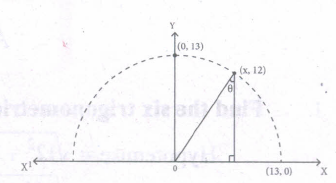
The parallel sides of a trapezium are 15 m and 10 m long and its non-parallel sides are 8 m and 7 m long. Find the area of the trapezium.

Find the area of an equilateral triangle whose perimeter is 150 m.

Two dice are rolled, find the probability that the sum is
(i) equal to 1
(ii) equal to 4
(iii) less than 13

Two unbiased coins are tossed simultaneously find the probability of getting
(i) two heads
(ii) one head
(iii) at least one head
(iv) at most one head

In a class there are 40 students. 26 have opted for Mathematics and 24 have opted for Science. How many student have opted for Mathematics and Science.

If A = {b,c,e,g,h}, B = {a,c,d,g,i} and C = {a,d,e,g,h}, then show that \(A-(B\cap C)=(A-B)\cup (A-C)\).

Express the following decimal expression into rational numbers \(3.1\overline { 7 } \)

Add \(\sqrt [ 5 ]{ 11 } \) and \(\sqrt [ 7 ]{ 11 } \). Check whether the sum is rational or irrational

The perimeter of a triangle is 8m² - 9m+ 7. If the two sides of the triangel be m² - m + 6 and 3m² - 2m - 4, find the third side.

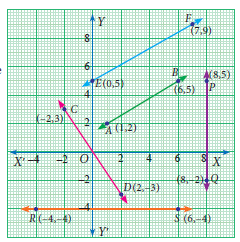
Find the slopes of all the lines from the adjacent figure,

The angles of quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.

Draw and locate the centroid of the triangle ABC where right angle at A, AB = 4cm and AC = 3cm

Let A(2, 3) and B(2, –4) be two points. If P lies on the x-axis, such that AP = \(\frac{3}{7}\) AB, find the coordinates of P.

Three vertices of a rectangle are (3, 2), (-4, 2) and (-4, 5). Plot the points and find the coordinates of the fourth vertex.

A researcher studying the behavior of mice has recorded the time (in seconds) taken by each mouse to locate its food by considering 13 different mice as 31, 33, 63, 33, 28, 29, 33, 27, 27, 34, 35, 28, 32. Find the median time that mice spent in searching its food.

Find the value of cos19⁰59'

The length, breadth and height of a cuboid are in the ratio 7: 5: 2. Its volume is 35840 cm³. Find its dimensions.

Team I and Team II play 10 cricket matches each of 20 overs. Their total scores in each match are tabulated in the table as follows:

Match numbers	1	2	3	4	5	6	7	8	9	10
Team I	200	122	111	88	156	184	99	199	121	156
Team II	143	123	156	92	164	72	100	201	98	157

What is the relative frequency of Team I winning?

Draw Venn diagram for \(A\cap B\cap C\)

Find any three rational numbers between \(\frac { 1 }{ 2 } \) and \(\frac { 1 }{ 5 } \)

Represent \(-\frac { 2 }{ 11 } ,-\frac { 5 }{ 11 } and-\frac { 9 }{ 11 } \)on the number line.

Prove that x -1 is a factor x⁵ - 45x⁴ + 36x³ + 45x² - 36x^-1

Diagonal AC of a parallelogram ABCD bisects ㄥA. Show that
(i) it bisects ㄥC also
(ii) ABCD is a rhombus.

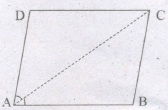
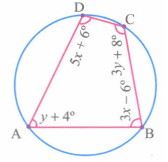
Find the angle of the given cyclic quadrilateral ABCD in the figure.

Show that the point (3, -2), (3, 2), (-1, 2) and (-1, -2) taken in order are the vertices of a square.

Calculate the mean of the following distribution using Assumed Mean Method

Class Interval	0-10	10-20	20-30	30-40	40-50
Frequency	5	7	15	28	8

A farmer has a field in the shape of a rhombus. The perimeter of the field is 400 m and one of its diagonal is 120 m. He wants to divide the field into two equal parts to grow two different types of vegetables. Find the area of the field.