Which of the following is correct?

(a)

{7} ∈ {1,2,3,4,5,6,7,8,9,10}

(b)

7 ∈ {1,2,3,4,5,6,7,8,9,10}

(c)

7 ∉ {1,2,3,4,5,6,7,8,9,10}

(d)

{7} \(\nsubseteq \) {1,2,3,4,5,6,7,8,9,10}

The set {x: x ∈ A, x ∈ B, x ∉ A ∩ B} is___________.

(a)

A ∩ B

(b)

A U B

(c)

A - B

(d)

A Δ B

If n(A U B U C) = 100, n(A) = 4x, n(B) = 6x, n(C) = 5x, n(A ∩ B) = 20, n(B ⋂C) = 15, n(A C) = 25 and n(A ⋂ B ⋂ C) = 10 , then the value of x is ________.

(a)

10

(b)

15

(c)

25

(d)

30

If U = {x : x\(\in \)W and x < 20}, A = {2,4,6,8}, B = {6,8,12,14} then\(\left[ n\left( A\cup B^{ ' } \right) \right] \)

(a)

15%

(b)

20%

(c)

10%

(d)

5%

For any three sets, P,Q,R\(\left( P\cap Q \right) ^{ ' }\)

(a)

\({ P }^{ ' }\cup { Q }^{ ' }\)

(b)

\(P\cup Q\)

(c)

\({ P }^{ ' }\)

(d)

\({ Q }^{ ' }\)

The value of \(\bar { 0.03 } \) +\(\bar { 0.03 } \)  is ___________.

(a)

\(\bar { 0.09 } \)

(b)

\(\bar { 0.09 } \)

(c)

\(\bar { 0.09 } \)

(d)

0

\(\sqrt{27}\)+\(\sqrt{12}\) = ________.

(a)

\(\sqrt{39}\)

(b)

5\(\sqrt{6}\)

(c)

5\(\sqrt{3}\)

(d)

3\(\sqrt{5}\)

When written with a rational denominator, the expression \(\frac { 2\sqrt { 3 } }{ 3\sqrt { 2 } } \) can be simplified as ________.

(a)

\(\frac { \sqrt { 2 } }{ 3 } \)

(b)

\(\frac { \sqrt { 3 } }{ 2 } \)

(c)

\(\frac { \sqrt { 6 } }{ 3 } \)

(d)

\(\frac{2}{3}\)

\(\sqrt [ 5 ]{ 21 } \times 6\sqrt { 10 } \)

(a)

\(30\sqrt { 210 } \)

(b)

30

(c)

\(\sqrt { 210 } \)

(d)

\(210\sqrt { 30 } \)

Rationalising the denominator \(\cfrac { 1 }{ \sqrt [ 3 ]{ 3 } } \)  ___________

(a)

3

(b)

\(\cfrac { { 3 }^{ \frac { 2 }{ 3 } } }{ 3 } \)

(c)

\(\sqrt { 3 } \)

(d)

\(\sqrt [ 3 ]{ 3 } \)

x³ – x² is a …………..

(a)

monomial

(b)

binomial

(c)

trinomial

(d)

constant polynomial

The coefficient of \({ x }^{ 2 }\ and\ x\ in\ 2{ x }^{ 3 }-5{ x }^{ 2 }+6x-3\) are respectively ____________

(a)

2, -5

(b)

2, 6

(c)

-5, 6

(d)

-5, -3

The GCD of x⁴-y⁴ and x²-y² is _______.

(a)

x⁴-y⁴

(b)

x²-y²

(c)

(x+y)²

(d)

(x+y)⁴

Which of the following has a factor?

(a)

x² + 2x

(b)

(x - 1)²

(c)

(x + 1)²

(d)

(x² - 2²)

If x - 2 is a factor of q(x), then the remainder is___________

(a)

q(-2)

(b)

x - 2

(c)

0

(d)

-2

(a-b-c)² is equal to________

(a)

(a+b+c)²

(b)

(a+b+c)²

(c)

(-a + b + c)²

(d)

(a+b+c)²

If the diagonal of a rhombus are equal, then the rhombus is a ________.

(a)

Parallelogram but not a rectangle

(b)

Rectangle but not a square

(c)

Square

(d)

Parallelogram but not a square

What is the name of a regular polygon of six sides?

(a)

Square

(b)

Equilateral triangle

(c)

Regular hexagon

(d)

Regular octagon

In a parallelogram \(\angle{A}:\angle{B}=1:2\) Then ㄥA ............

(a)

30°

(b)

60°

(c)

45°

(d)

90°

Which of the following is a formula to find the sum of interior angles of a quadrilateral of n-sides?

(a)

\(\frac { n }{ 2 } \) \(\times\) 180

(b)

\(\left( \frac { n+1 }{ 2 } \right) \)180⁰

(c)

\(\left( \frac { n-1 }{ 2 } \right) \)180^o

(d)

(n-2)180^o

In the figure, PQRS and PTVS are two cyclic quadrilaterals, If ㄥQRS = 100°, then ㄥTVS = ______.

(a)

80°

(b)

100°

(c)

70°

(d)

90°

If sum of two opposite angles of a cyclic quadrilateral is_________

(a)

45°

(b)

90°

(c)

180°

(d)

360°

If P( –1, 1), Q( 3, -4), R( 1,  -1), S(-2, -3) and T( -4, 4) are plotted on a graph paper, then the points in the fourth quadrant are ______.

(a)

P and T

(b)

Q and R

(c)

only S

(d)

P and Q

The centre of a circle is (0, 0). One end point of a diameter is (5, -1), then ______________

(a)

\(\sqrt{24}\)

(b)

\(\sqrt{37}\)

(c)

\(\sqrt{26}\)

(d)

\(\sqrt{17}\)

The point (0, -3) lies on _______________

(a)

+ ve x-axis

(b)

+ ve y-axis

(c)

- ve x-axis

(d)

- ve y-axis

The point which is on y-axis with ordinate - 5 is _____________

(a)

(0, - 5)

(b)

(-5,0)

(c)

(5,0)

(d)

(0,5)

The diagonal of a square formed by the points (1, 0), (0, 1), (-1, 0) and (0, - 1) is_______________

(a)

2

(b)

4

(c)

\(\sqrt{2}\)

(d)

8

The mid-point of the line joining (−a, 2b) and (−3a,−4b) is ______.

(a)

(2a, 3b)

(b)

(−2a, −b)

(c)

(2a, b)

(d)

(−2a, −3b)

A particular observation which occurs maximum number of times in a given data is called its _______.

(a)

Frequency

(b)

range

(c)

mode

(d)

Median

For which set of numbers do the mean, median and mode all have the same values?

(a)

2, 2, 2, 4

(b)

1, 3, 3, 3, 5

(c)

1, 1, 2, 5, 6

(d)

1, 1, 2, 1, 5

For which set of number do the mean,median and mode all have the same valuas?

(a)

2,2,2,4

(b)

1,3,3,3,5

(c)

1,1,2,5,6

(d)

1,1,2,1,5

If the mean of five observations x, x+2, x+4, x+6, x+8, is 11, then the mean of first three observations is __________

(a)

9

(b)

11

(c)

13

(d)

15

The mean of the first 10 prime number is _______________

(a)

12.6

(b)

12.7

(c)

12.8

(d)

12.9

Find the mean of the prime factors of 165 _____________

(a)

5

(b)

11

(c)

13

(d)

55

The value of \(\frac { tan15° }{ cot75° } \) is

(a)

cos 90⁰

(b)

sin 30⁰

(c)

tan 45⁰

(d)

cos 30⁰

The value of tan 1° tan 2° tan 3°...tan 89° is ________.

(a)

0

(b)

1

(c)

2

(d)

\(\frac { \sqrt { 3 } }{ 2 } \)

If the sides of a triangle are 3 cm, 4 cm and 5 cm, then the area is _______.

(a)

3 cm²

(b)

6 cm²

(c)

9 cm²

(d)

12 cm²

The number of bricks each measuring 50 cm × 30 cm × 20 cm that will be required to build a wall whose dimensions are 5 m × 3 m × 2 m is _______.

(a)

1000

(b)

2000

(c)

3000

(d)

5000

The probability of all possible outcomes of a random experiment is always equal to _______.

(a)

One

(b)

Zero

(c)

Infinity

(d)

Less than one

A collection of one or more outcomes of an experiment is called _______.

(a)

Event

(b)

Outcome

(c)

Sample point

(d)

None of the above

From the given Venn diagram, write the elements of

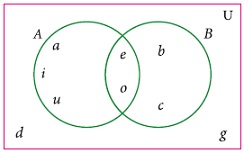
(i) A
(ii) B
(iii) A – B
(iv) B – A
(v) A′
(vi) B′
(vii) U

IfA = {1,2,3} B = {3,5,6} C = {3,4,7}. Find
(i) A-(BUC)
(ii) BΔC
(iii) AΔB

Let U= {x : -3 : < x < 4} A = {-1,2,3} B = {0,1,2,3} C = {-3;-2,-1,0,1,2}. Find (i) A' UB' (ii) (A ∩ B)' (iii) (A ⋂ C)'

If A =\(\left\{ -\frac { 1 }{ 2 } ,0,\frac { 1 }{ 4 } ,\frac { 3 }{ 4 } ,2 \right\} \), B =\(\left\{ 0,\frac { 1 }{ 4 } ,\frac { 3 }{ 4 } ,2,\frac { 5 }{ 2 } \right\} \) and C =\(\left\{ -\frac { 1 }{ 2 } .\frac { 1 }{ 4 } ,1,2,\frac { 5 }{ 2 } \right\} \), then verify \(A\cap (B\cap C)=(A\cap B)\cap C\) .

Use a fractional index to write: \(\sqrt{5}\)

Evaluate : \(\left( \cfrac { 1 }{ 9 } \right) ^{ -3 }\)

Express the surds in the simple form \(\sqrt { 27 } \)

Represent the following as decimal form 
(i) \(\frac { -4 }{ 11 } \)
(ii) \(\frac { 11 }{ 75 } \)

Verify whether the following are zeros of the polynomial indicated against them, or not.
p(x) = (x+3) (x-4), x = -3, x = 4

Factorise the following : 64m³ + 27n³

Akshaya has 2 rupee coins and 5 rupee coins in her purse. If in all she has 80 coins totalling Rs. 220, how many coins of each kind does she have.

Identify which ones are trapeziums and which are not.

Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord

The chord of length 32 cm is drawn at the distance of 12 cm from the centre of the circle. Find the radius of the circle

In a circle, AB and CD are two parallel chords with centre 0 and radius 5 em such that AB = 8 cm and CD = 6 cm determine the distance between the chords?

Using section formula, show that the points A(7, −5), B(9, −3) and C(13, 1) are collinear.

Find the coordinates of the point which divides the line segment joining the points (3, 1) and (5, 13) internally in the ratio 3 : 5.

In a rice mill, seven labours are receiving the daily wages of Rs. 500, Rs. 600, Rs. 600, Rs. 800, Rs. 800, Rs. 800 and Rs. 1000, find the modal wage

The mean weight of 4 members of a family is 60 kg. Three of them have the weight 56kg, 68kg and 72 kg respectively. Find the weight of the fourth member.

Evaluate: 
(i) sin 30⁰ +cos 30⁰
(ii) tan 60⁰ cot 60⁰
(iii) \(\frac { tan45° }{ tan30°+tan60° } \)
(iv) sin² 45⁰ +cos² 45⁰

Find the value of \(\cfrac { cos{ 63 }^{ 0 }20' }{ sin{ 26 }^{ 0 }40' } \)

The parallel sides of a trapezium are 15 m and 10 m long and its non-parallel sides are 8 m and 7 m long. Find the area of the trapezium.

Find the surface area of a cube whose edge is
(i) 27 cm
(ii) 3 cm
(iii) 6 cm
(iv) 2.1 cm

A company manufactures 10000 Laptops in 6 months. In that 25 of them are found to be defective. When you choose one Laptop from the manufactured, what is the probability that selected Laptop is a good one.

One card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that the card drawn is
(i) an ace,
(ii) either red card or king.

In a class there are 40 students. 26 have opted for Mathematics and 24 have opted for Science. How many student have opted for Mathematics and Science.

If U = {x : x ∈ Z, -2 ≤ x ≤ 10}, A = {x : x = 2p +1, p ∈ Z, -1 ≤ p ≤ 4}, B = {x : x = 3q + 1, q ∈ Z, -1 ≤ q < 4} verify De Morgan’s laws for complementation.

Express the following decimal expression into rational numbers \(17.2\overline { 15 } \)

Sho that \(\sqrt [ 3 ]{ 2 } >\sqrt [ 5 ]{ 3 } \)

What must be subtracted from \({ y }^{ 4 }+{ 2y }^{ 3 }-3y+8\quad to\quad get\quad { y }^{ 4 }-{ 2y }^{ 3 }+6?\)

(i) Prove that (x - 1) is a factor of x³- 7x² + 13x - 7
(ii) Prove that (x + 1) is a factor of x³ + 7x² + 13x + 7

ABCD is a parallelogram and AP and CQ are perpendic from vertex A and C on diagonal BD. Show that
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ

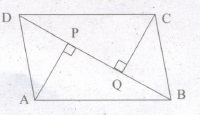
Draw and locate the centroid of the triangle ABC where right angle at A, AB = 4cm and AC = 3cm

The abscissa of a point A is equal to its ordinate, and its distance from the point B(1, 3) is 10 units, What are the coordinates of A?

Three vertices of a rectangle are (3, 2), (-4, 2) and (-4, 5). Plot the points and find the coordinates of the fourth vertex.

The arithmetic mean of 6 values is 45 and if each value is increased by 4, then find the arithmetic mean of new set of values

The following are scores obtained by 11 players in a cricket match 7, 21, 45, 12, 56, 35, 25, 0, 58, 66, 29. Find the median score.

Evaluate:
(i) \(\frac { sin\ 49° }{ cos\ 41° } \) 
(ii) \(\frac { sec\ 63° }{ cosec\ 27° } \)

Find the Total Surface Area and Lateral Surface Area of the cube, whose side is 5 cm.

In an office, where 42 staff members work, 7 staff members use cars, 20 staff members use two-wheelers and the remaining 15 staff members use cycles. Find the relative frequencies.

Fill in the blanks with appropriate cardinal numbers

S.No	n(A)	n(B)	n(AUB)	n(A∩B)	n(A-B)	n(B-A)
1	30	45	65
2	20		55	10
3	50	65		25
4	30	43	70

Find any three rational numbers between \(\frac { 1 }{ 2 } \) and \(\frac { 1 }{ 5 } \)

Represent \(-\frac { 2 }{ 11 } ,-\frac { 5 }{ 11 } and-\frac { 9 }{ 11 } \)on the number line.

Factorise  2x³- x² - 12x - 9 into linear factors
 

Find the angle of the given cyclic quadrilateral ABCD in the figure.

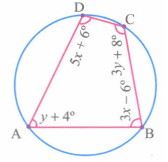
Construct  \(\triangle\)ABC in which AB = BC = 8cm and \(\angle \)B =70^o. Locate its in centre and draw the incircle
 

Show that the given points (1, 1), (5, 4), (-2, 5) are the vertices of an isosceles right angled triangle.

In the class, weight of students is measured for the class records. Caculate mean weight of the students using direct method.

Weight in kg	15-25	25-35	35-45	45-55	55-65	56-75
No.of students	4	11	19	14	0	2

Find the Arithmetic Mean of the following data using Step Deviation Method

Age	15-19	20-24	25-29	30-34	35-39	40-44
No.of persons	4	20	38	24	10	9

A farmer has a field in the shape of a rhombus. The perimeter of the field is 400 m and one of its diagonal is 120 m. He wants to divide the field into two equal parts to grow two different types of vegetables. Find the area of the field.