The shaded region in the adjacent diagram represents ______________

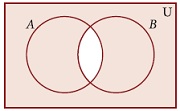(a)

(A∪B)′

(b)

(A∩B)′

(c)

A′∩B′

(d)

A∩B

If X = {x : x = 4(n – 1), n ∈ N} and Y = {y : y = 3n – 2n – 1, n ∈ N}, then X∪Y is ______________

(a)

W

(b)

X

(c)

Y

(d)

N

A = {set of odd natural numbers}, B = {set of even natural numbers}, then A and B are ___________

(a)

equal set

(b)

equivalent sets

(c)

overlapping sets

(d)

disjoint sets

The set does not have a proper subset is __________

(a)

Finite set

(b)

Infinite set

(c)

Null set

(d)

Singleton set

If A,B,C are non-overlapping sets, then n \(\left( A\cap B\cap C \right) \) is ___________

(a)

n(A) + n(B) + n(C)

(b)

\(n\left( A\cup B\cup C \right) \)

(c)

0

(d)

\(n\left( A\cap B \right) \)

Find the odd one out of the following.

(a)

\(\sqrt { 32 } \times \sqrt { 2 } \)

(b)

\(\frac { \sqrt { 27 } }{ \sqrt { 3 } } \)

(c)

\(\sqrt { 72 } \times \sqrt { 8 } \)

(d)

\(\frac { \sqrt { 54 } }{ \sqrt { 18 } } \)

The decimal form of -\(\frac { 3 }{ 4 } \) is_______________

(a)

- 0.75

(b)

- 0.50

(c)

-0.25

(d)

- 0.125

The product of \(2\sqrt { 5 } \) and \(6\sqrt { 5 } \) is_______________.

(a)

\(12\sqrt { 5 } \)

(b)

60

(c)

40

(d)

\(8\sqrt { 5 } \)

What is 5.92 \(\times\)10^-3 written in decimal form?

(a)

0.000592

(b)

0.00592

(c)

0.0592

(d)

0.592

Rationalising the denominator \(\cfrac { 1 }{ \sqrt [ 3 ]{ 3 } } \)  ___________

(a)

3

(b)

\(\cfrac { { 3 }^{ \frac { 2 }{ 3 } } }{ 3 } \)

(c)

\(\sqrt { 3 } \)

(d)

\(\sqrt [ 3 ]{ 3 } \)

The root of the polynomial equation 2x + 3 = 0 is ________.

(a)

\(\frac{1}{3}\)

(b)

\(-\frac{1}{3}\)

(c)

\(-\frac{3}{2}\)

(d)

\(-\frac{2}{3}\)

The type of the polynomial 4–3x³ is  ________.

(a)

constant polynomial

(b)

linear polynomial

(c)

quadratic polynomial

(d)

cubic polynomial.

The roots of the polynominal equation \({ x }^{ 2 }+2x=0\) are_______________

(a)

x = 0, 2

(b)

x = 1, 2

(c)

x = 1, -2

(d)

x = 0, -2

The value of the polynomial f(x) = 6x - 3x²+9 when x = -1 is _____________________

(a)

0

(b)

1

(c)

2

(d)

3

Divide x³-4x²+6x by "x" the result is _____________________

(a)

\(x^{ 2 }+4x-6\)

(b)

\(x^{ 2 }-4x-6\)

(c)

\(x^{ 2 }-4x+6\)

(d)

\(x^{ 2 }+4x+6\)

If one of the factor of x^2-9x+18 is (x-3) then the other factor is_________

(a)

x-9

(b)

x+6

(c)

(x-6)

(d)

x-18

The correct statement out of the following is ________.

(a)

ΔABC ≅ ΔDEF

(b)

ΔABC ≅ ΔDEF

(c)

ΔABC ≅ ΔFDE

(d)

ΔABC ≅ ΔFED

Orthocentre of a triangle is the point of concurrency of _______

(a)

medians

(b)

altitudes

(c)

angle bisectors

(d)

perpendicular bisectors of side

ABCD is a parallelogram as shown. Find x and y.

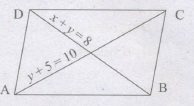(a)

1, 7

(b)

2, 6

(c)

3, 5

(d)

4, 4

In the given figure, If OP = 17cm PQ = 30, cm and OS is perpendicular to PQ, then RS is ________.

(a)

10 cm

(b)

6 cm

(c)

7 cm

(d)

9 cm

In the figure, PQRS and PTVS are two cyclic quadrilaterals, If  \(\angle\)QRS = 70°, then \(\angle\)TVS= __________

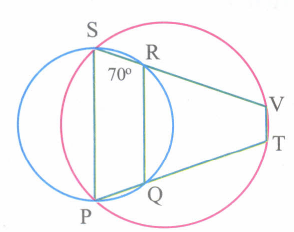(a)

70°

(b)

110°

(c)

80°

(d)

90°

The distance between the longest chord of a circle and the centre is________

(a)

1

(b)

0

(c)

2

(d)

5

If ( x+2, 4) = (5, y–2), then the coordinates (x,y) are _____.

(a)

(7, 12)

(b)

(6, 3)

(c)

(3, 6)

(d)

(2, 1)

A point on the y-axis is ________________

(a)

(1, 1)

(b)

(6,0)

(c)

(0,6)

(d)

(-1, -1)

The distance between the points (a, 0) and (0, b) is____________

(a)

a unit

 

(b)

b unit

(c)

\(\sqrt{a^2+{b^2}}\ unit\)

(d)

\(\sqrt{a^2-{b^2}}\ unit\)

The point (0, -3) lies on _______________

(a)

+ ve x-axis

(b)

+ ve y-axis

(c)

- ve x-axis

(d)

- ve y-axis

The diagonal of a square formed by the points (1, 0), (0, 1), (-1, 0) and (0, - 1) is_______________

(a)

2

(b)

4

(c)

\(\sqrt{2}\)

(d)

8

If the coordinates of the mid-points of the sides AB, BC and CA of a triangle are (3, 4), (1, 1) and (2, −3) respectively, then the vertices A and B of the triangle are ______.

(a)

(3, 2), (2, 4)

(b)

(4, 0), (2, 8)

(c)

(3, 4), (2, 0)

(d)

(4, 3), (2, 4)

The mean of 5, 9, x, 17, and 21 is 13, then find the value of x _______.

(a)

9

(b)

13

(c)

17

(d)

21

The mean of the first 10 prime numbers is ___________

(a)

12.6

(b)

12.7

(c)

12.8

(d)

12.9

The mean of set of seven number is 81. If one of the nimbers is discarded,the mean of remaining number is 78. The value of discarded number is

(a)

101

(b)

100

(c)

99

(d)

98

The algebraic sum of the deviations of a set of n values from their mean is ___________

(a)

0

(b)

n-1

(c)

n

(d)

n+1

The mean of the first 10 whole number is

(a)

4

(b)

4.5

(c)

5

(d)

5.5

The mean of set of numbers is \(\bar{x}\) If each number is multiplied by z, the mean is

(a)

\(\bar{X}+z\)

(b)

\(\bar{X}-z\)

(c)

\(z\bar{X}\)

(d)

\(\bar{X}\)

The value of 2tan30° tan60° is

(a)

1

(b)

2

(c)

\(2\sqrt { 3 } \)

(d)

6

The value of \(\frac { 1-{ tan }^{ 2 }{ 45 }^{ 0 } }{ 1+{ tan }^{ 2 }{ 45 }^{ 0 } } \) is ________.

(a)

2

(b)

1

(c)

0

(d)

\(\frac { 1 }{ 2 } \)

The lateral surface area of a cube of side 12 cm is _______.

(a)

144 cm²

(b)

196 cm²

(c)

576 cm²

(d)

664 cm²

The capacity of a water tank of dimensions 10 m × 5 m × 1.5 m is _______.

(a)

75 litres

(b)

750 litres

(c)

7500 litres

(d)

75000 litres

The probability based on the concept of relative frequency theory is called _______.

(a)

Empirical probability

(b)

Classical probability

(c)

Both (1) and (2)

(d)

Neither (1) nor (2)

A letter is chosen at random from the word “STATISTICS”. The probability of getting a vowel is

(a)

\(\frac { 1 }{ 10 } \)

(b)

\(\frac { 2 }{ 10 } \)

(c)

\(\frac { 3 }{ 10 } \)

(d)

\(\frac { 4 }{ 10 } \)

Are A = {x : x ∈ N, 4 ≤ x ≤ 8} and B = { 4, 5, 6, 7, 8} equal sets?

If n(A) = 25, n(B) = 40, n(A∪B) = 50 and n(B′) = 25 , find n(A∩B) and n(U).

Write the following in "Roster" form?
(a) A = set of the months having 31 days.
(b) B = {x : x is a natural number of 2 digits divisible by 13}
(c) C = {set of vowels in the word "father"}
(d) D = {x : 5 < x < 10 ; x ∈ N}
(e) E = {x: x is a square natural number less than 16}

State Associative property of sets.

you know that \(\frac { 1 }{ 7 } \)= 0.142857. Can you predict what the decimal expansion of \(\frac { 2 }{ 7 } ,\frac { 3 }{ 7 } ,\frac { 5 }{ 7 } ,\frac { 6 }{ 7 } \) are without actually doing the long division. If so, how?

Without actual division classify the decimal expansion of the following numbers as terminating or non-terminating and recurring.
\(7\over 16\)

Divide \(\sqrt [ 9 ]{ 8 } \) by \(\sqrt [ 6 ]{ 6 } \).

Find any 3 irrational numbers between 0.12 and 0.13.

Using factor theorem, show that (x -5) is a factor of the polynomial 2x³-5x²-28x+15

On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains Rs. 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss, he gains Rs. 1500 on the transaction. Find the actual price of the T.V. and the fridge.

Find the value of k for which the system of linear equations has no solution
ka+ 10b = 15, 8a+5b=9

Find the value of x

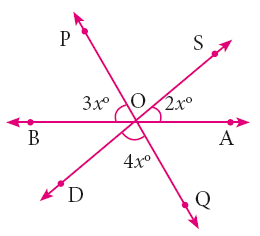
In the given diagram PQRS is a parallelogram.
ㄥS = 4x - 60, ㄥQ = 30 - x. Find the angles of P and R.

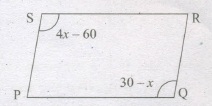
In figure ㄥABC = 120⁰, where A, B and C are points on the circle with centre O. Find ㄥOAC?

The chord of length 32 cm is drawn at the distance of 12 cm from the centre of the circle. Find the radius of the circle

Find the centroid of the triangle whose vertices are
(i) (2, −4), (−3, −7) and (7, 2)
(ii) (−5, −5), (1, −4) and (−4, −2)

Find the centroid of the triangle whose vertices are (2, -5), (5, 11) and (9, 9)

A set of numbers consists of five 4’s, four 5’s, nine 6’s,and six 9’s. What is the mode.

In a class test in mathematics,10 students scored 75 marks,12 students scored 60 mark, 8 students scored 40 marks and 3 students scored 30 marks. Find the mean of their score.

If cos \(\theta\) : sin\(\theta\) =1: 2, then find the value of = \(\frac { 8cos\theta -2sin\theta }{ 4cos\theta +2sin\theta } \)

If 3 (tan \(\theta\)) + 4 (sec \(\theta\) \(\times\) sin 6) = 24. Then find all the trigonometric ratios of the angle \(\theta\)

An advertisement board is in the form of an isosceles triangle with perimeter 36m and each of the equal sides are 13 m. Find the cost of painting it at Rs. 17.50 per square metre.

Find the TSA and LSA of a cuboid whose length, breadth and height are 10 cm, 12 cm and 14 cm respectively.

Frame two problems in calculating probability, based on the spinner shown here.

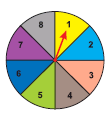
Find the probability that a leap year selected at random will contain 53 Sundays.

Given that A = {1,3,5,7} B = {1,2,4,6,8}. Find
(i) AΔB and
(ii) BΔA

If U = {x : x ∈ Z, -2 ≤ x ≤ 10}, A = {x : x = 2p +1, p ∈ Z, -1 ≤ p ≤ 4}, B = {x : x = 3q + 1, q ∈ Z, -1 ≤ q < 4} verify De Morgan’s laws for complementation.

Express the following decimal expression into rational numbers \(17.2\overline { 15 } \)

Compute and give the answer in the simplest form; \(3\sqrt { 162 } \times 7\sqrt { 50 } \times 6\sqrt { 98 } \)

If the quotient obtained on dividing 3x³+11x²+34x+106 by x - 3 is 3x²+ ax + b then find a, b and also the remainder.

Find the GCD of a^x, a^x+y, a^x+y+z

Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent:

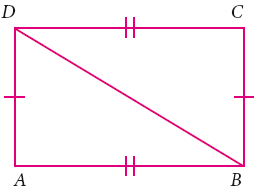
ABCD is a parallelogram and AP and CQ are perpendic from vertex A and C on diagonal BD. Show that
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ

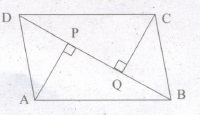
Three vertices of a rectangle are (3, 2), (-4, 2) and (-4, 5). Plot the points and find the coordinates of the fourth vertex.

Join the points taken in order and name the figure obtained. Name atleast any one point which is lying :
(i)On x-axis 
(ii)On y-axis
(iii) In each of the Quadrants.

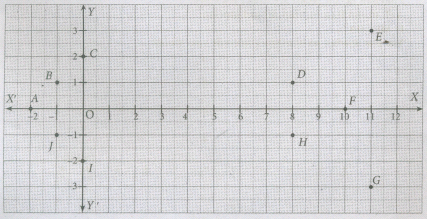
Find the mean of the following distribution using Step Deviation Method.

Class Interval	0-8	8-16	16-24	24-32	32-40	40-48
Frequency (f)	10	20	14	16	18	22

Find the values of
(i) tan7° tan23° tan60° tan67° tan83°  
(ii) \(\frac { cos35° }{ sin55° } +\frac { sin12° }{ cos78° } -\frac { cos18° }{ sin72° } \)

The total surface area of a cube is 864 cm². Find its volume

Team I and Team II play 10 cricket matches each of 20 overs. Their total scores in each match are tabulated in the table as follows:

Match numbers	1	2	3	4	5	6	7	8	9	10
Team I	200	122	111	88	156	184	99	199	121	156
Team II	143	123	156	92	164	72	100	201	98	157

What is the relative frequency of Team I winning?

If A, Band C are overlapping sets, draw venn diagram for:\(A\cap B\)

Find any  seven rational numbers between \(\frac { 5 }{ 8 } \) and \(\frac { 5 }{ 6 } \)

Find any three rational numbers between \(\frac { 1 }{ 2 } \) and \(\frac { 1 }{ 5 } \)

Prove that x -1 is a factor x⁵ - 45x⁴ + 36x³ + 45x² - 36x^-1

Draw an equilateral triangle of side 8 cm and locate its incentre. Also draw the incircle.

Construct  \(\triangle\)ABC in which AB = BC = 8cm and \(\angle \)B =70^o. Locate its in centre and draw the incircle
 

Find the type of triangle formed by (-1, -1), (1, 1) and (\(-\sqrt{13},\sqrt{13}\))

Find the Arithmetic Mean of the following data using Step Deviation Method

Age	15-19	20-24	25-29	30-34	35-39	40-44
No.of persons	4	20	38	24	10	9

The mean of five positive integers is twice their median.If four of the integers are 3, 4, 6, 9 and median is 6, then find the fifth integer.

A farmer has a field in the shape of a rhombus. The perimeter of the field is 400 m and one of its diagonal is 120 m. He wants to divide the field into two equal parts to grow two different types of vegetables. Find the area of the field.