If X = {x : x = 4(n – 1), n ∈ N} and Y = {y : y = 3n – 2n – 1, n ∈ N}, then X∪Y is ______________

(a)

W

(b)

X

(c)

Y

(d)

N

A = {set of odd natural numbers}, B = {set of even natural numbers}, then A and B are ___________

(a)

equal set

(b)

equivalent sets

(c)

overlapping sets

(d)

disjoint sets

Sets having the same number of elements are called ___________

(a)

overlapping sets

(b)

disjoints sets

(c)

equivalent sets

(d)

equal sets

The set of (A U B) - (A ก B) is ____________

(a)

(AUB)'

(b)

AΔB

(c)

(A∩B)'

(d)

A'UB'

If n(A \(\cup \) B \(\cup \) C) = 40, n(A) = 30, n(B) = 25, n(C) = 20, n(A\(\cap \)B) = 12, n(B\(\cap \)C) = 18 and n(A\(\cap \)C) = 15 , then n(A\(\cap \)B\(\cap \)C) is ___________

(a)

5

(b)

10

(c)

15

(d)

20

Which one of the following, regarding sum of two irrational numbers, is true?

(a)

always an irrational number

(b)

may be a rational or irrational number

(c)

always a rational number

(d)

always an integer.

The decimal form of -\(\frac { 3 }{ 4 } \) is_______________

(a)

- 0.75

(b)

- 0.50

(c)

-0.25

(d)

- 0.125

Which of the following are irrational numbers?
\(\sqrt { 2+\sqrt { 3 } } \)
\(\sqrt [ 3 ]{ 5+\sqrt { 7 } } \)
\(\sqrt { 8-\sqrt [ 3 ]{ 8 } } \)
\(\sqrt { 4+\sqrt { 25 } } \)

(a)

(ii), (iii) and (iv)

(b)

(i), (ii) and (iv)

(c)

(i), (ii) and (iii)

(d)

(i), (iii) and (iv)

If \(\sqrt { { 9 }^{ x } } =\sqrt [ 3 ]{ 9^{ 2 } } \) , then x = _______.

(a)

\(\frac{2}{3}\)

(b)

\(\frac{4}{3}\)

(c)

\(\frac{1}{3}\)

(d)

\(\frac{5}{3}\)

Which is the best example of a number written in scientific notation?

(a)

2.71 \(\times\) 10⁵

(b)

0.6 \(\times\) 10⁴

(c)

0.9871

(d)

125.4 \(\times\) 10⁴

If x³ + 6x² + kx + 6 is exactly divisible by (x + 2), then k= ?

(a)

-6

(b)

-7

(c)

-8

(d)

11

if a polynominal p(x) is divided by (ax+b), then the reminder is _______________________

(a)

\(p\left( \frac { b }{ a } \right) \)

(b)

\(p\left( -\frac { b }{ a } \right) \)

(c)

\(p\left( \frac { a }{ b } \right) \)

(d)

\(p\left( -\frac { a }{ b } \right) \)

(a-b-c)² is equal to________

(a)

(a+b+c)²

(b)

(a+b+c)²

(c)

(-a + b + c)²

(d)

(a+b+c)²

Degree of the linear polynomial is ________

(a)

1

(b)

2

(c)

3

(d)

4

If one of the factor of x^2-9x+18 is (x-3) then the other factor is_________

(a)

x-9

(b)

x+6

(c)

(x-6)

(d)

x-18

Which of the following is a solution of the equation 2x − y = 6.

(a)

(2,4)

(b)

(4,2)

(c)

(3, −1)

(d)

(0,6)

The correct statement out of the following is ________.

(a)

ΔABC ≅ ΔDEF

(b)

ΔABC ≅ ΔDEF

(c)

ΔABC ≅ ΔFDE

(d)

ΔABC ≅ ΔFED

The interior angle made by the side in a parallelogram is 90° then the parallelogram is a ________.

(a)

rhombus

(b)

rectangle

(c)

trapezium

(d)

kite

One angle of a parallelogram is a right angle. The name of the quadrilateral is ______

(a)

square

(b)

rectangle

(c)

rhombus

(d)

kite

The point of concurrency of the medians of a triangle is known as __________

(a)

circumcentre

(b)

incentre

(c)

orthocentre

(d)

centroid

The angle subtend by equal chords of a circle at the centre is________

(a)

Complementary

(b)

Supplementary

(c)

equal

(d)

unequal

The angle in a semi circle is_________

(a)

180°

(b)

90°

(c)

60°

(d)

45°

Point (–10, 0) lies ___________

(a)

on the negative direction of x-axis

(b)

on the negative direction of y-axis

(c)

in the III quadrant

(d)

in the IV quadrant

The point whose abscissa is 5 and lies on the x-axis is__________

(a)

(-5, 0)

(b)

(5,5)

(c)

(0,5)

(d)

(5,0)

The distance between the points (4, -1) and the origin is___________

(a)

\(\sqrt{24}\)

(b)

\(\sqrt{37}\)

(c)

\(\sqrt{26}\)

(d)

\(\sqrt{17}\)

The distance between the points (a, 0) and (0, b) is____________

(a)

a unit

 

(b)

b unit

(c)

\(\sqrt{a^2+{b^2}}\ unit\)

(d)

\(\sqrt{a^2-{b^2}}\ unit\)

The point which is on y-axis with ordinate - 5 is _____________

(a)

(0, - 5)

(b)

(-5,0)

(c)

(5,0)

(d)

(0,5)

If the coordinates of the mid-points of the sides AB, BC and CA of a triangle are (3, 4), (1, 1) and (2, −3) respectively, then the vertices A and B of the triangle are ______.

(a)

(3, 2), (2, 4)

(b)

(4, 0), (2, 8)

(c)

(3, 4), (2, 0)

(d)

(4, 3), (2, 4)

The mean of the square of first 11 natural numbers is _______.

(a)

26

(b)

46

(c)

48

(d)

52

The mean of a set of numbers is \(\bar X\). If each number is multiplied by z, the mean is _______.

(a)

\(\bar X + z\)

(b)

\(\bar X-z\)

(c)

z\(\bar X\)

(d)

\(\bar X\)

A particular observation which occurs maximum number of times in a given data is called is

(a)

Frequency

(b)

range

(c)

mode

(d)

median

For which set of number do the mean,median and mode all have the same valuas?

(a)

2,2,2,4

(b)

1,3,3,3,5

(c)

1,1,2,5,6

(d)

1,1,2,1,5

The algebraic sum of the deviations of a set of n values from their mean is ___________

(a)

0

(b)

n-1

(c)

n

(d)

n+1

The mean of a, b, c, d and e is 28. If the mean of a, c and e is 24, then mean of b and d is _______________

(a)

24

(b)

36

(c)

26

(d)

34

if sin 30⁰ = x and cos 60⁰ = y, then x²  + y² is________.

(a)

\(\frac { 1 }{ 2 } \)

(b)

0

(c)

sin90°

(d)

cos90°

The value of 2tan30° tan60° is

(a)

1

(b)

2

(c)

\(2\sqrt { 3 } \)

(d)

6

The perimeter of an equilateral triangle is 30 cm. The area is _______.

(a)

\(10\sqrt { 3 } \) cm²

(b)

\(12\sqrt { 3 } \) cm²

(c)

\(15\sqrt { 3 } \) cm²

(d)

\(25\sqrt { 3 } \) cm ²

The total surface area of a cuboid is ______________

(a)

4a² sq. units

(b)

6a² sq. units

(c)

2(l + b)h sq. units

(d)

2(lb + bh + lh) sq. units

A number between 0 and 1 that is used to measure uncertainty is called _______.

(a)

Random variable

(b)

Trial

(c)

Simple event

(d)

Probability

The probability of all possible outcomes of a random experiment is always equal to _______.

(a)

One

(b)

Zero

(c)

Infinity

(d)

Less than one

Draw Venn diagram and shade the region representing the following sets
(A – B)′

Find the symmetric difference between the following sets. P = {2, 3, 5, 7, 11} and Q = {1, 3, 5, 11}

Write the following in "Roster" form?
(a) A = set of the months having 31 days.
(b) B = {x : x is a natural number of 2 digits divisible by 13}
(c) C = {set of vowels in the word "father"}
(d) D = {x : 5 < x < 10 ; x ∈ N}
(e) E = {x: x is a square natural number less than 16}

IfA = {1,2,3} B = {3,5,6} C = {3,4,7}. Find
(i) A-(BUC)
(ii) BΔC
(iii) AΔB

Without actual division classify the decimal expansion of the following numbers as terminating or non-terminating and recurring.
\(-{11\over 75}\)

Find the value of \({ 64 }^{ \frac { -2 }{ 3 } }\)

Rationalise the denominator of (i) \(\frac { 7 }{ \sqrt { 14 } } \) (ii) \(\frac { 5+\sqrt { 3 } }{ 5-\sqrt { 3 } } \)

Evaluate : \(\left( \cfrac { 1 }{ 9 } \right) ^{ -3 }\)

Find the expansion of the following: (x + 4) (x + 5) (x + 6)

Factorise the following: l³- 8m³-27n³-18lmn

Factorise the following : 25m^-2-16n²

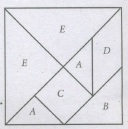
This is a copy of the tangram puzzle. The tangram puzzle consists of 7 geometric pieces which are normally boxed in the shape·of a square. The pieces, called 'tans', are used to create different patterns including animals, people, numbers, geometric shapes and many more.
You can make several polygons using the pieces in different ways.

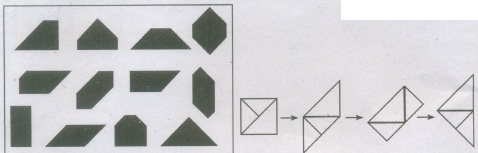
Draw the following special quadrilaterals on a graph sheet, measure the sides and angles and complete the table to explore the properties of the quadrilaterals with respect to sides and angles.

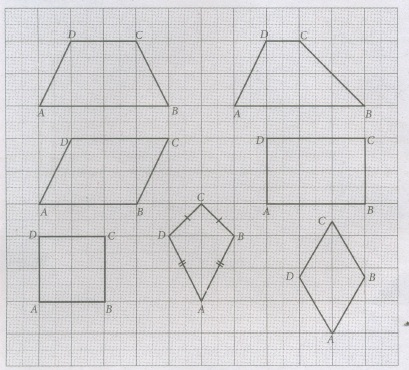
Find the value of X^o

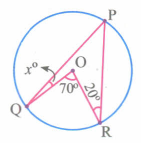
Find the value of X^o

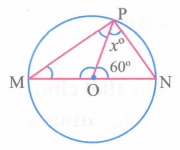
Find the coordinates of the point which divides the line segment joining the points A(4,−3) and B(9,7) in the ratio 3:2.

Using section formula, show that the points A (7, -5), B (9, -3) and C (13, 1), are collinear.

In a rice mill, seven labours are receiving the daily wages of Rs. 500, Rs. 600, Rs. 600, Rs. 800, Rs. 800, Rs. 800 and Rs. 1000, find the modal wage

In a research laboratory scientists treated 6 mice with lung cancer using medicine. Ten days, they measured the volume of the tumor of the tumor in each mouse given the results in the table

Mouse marking	1	2	3	4	5	6
Tumor Volume(mm)3	145	148	142	141	139	140

Find the mean

From the given figure, find all the trigonometric ratios of angle B.

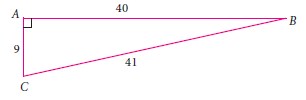
Find the value of \(\frac{\tan 25^{\circ}}{\cot 65^{\circ}}+\frac{\sin 40^{\circ}}{\cos 50^{\circ}}\)

The length, breadth and height of a chocolate box are in the ratio 5:4:3. If its volume is 7500 cm³, then find its dimensions.

A cuboid has total surface area of 40m² and its lateral surface area is 26 m², Find the area of its base.

The probability of guessing the correct answer to a certain question is \(\frac { x }{ 3 } \). If the probability of not guessing the correct answer is \(\frac { x }{ 5 } \), then find the value of x.

One card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that the card drawn is
(i) an ace,
(ii) either red card or king.

If A = {2,5,6,7} and B = {3,5,7,8}, then verify the commulative property of intersection of sets

Verify A -(BUC) = (A-B)∩(A-C) using Venn diagrams.

Express the following decimal expression into rational numbers \(3.1\overline { 7 } \)

Write in scientific notation: (500000)⁵\(\times\)(3000)³

Find the quotient and the remainder when (5x²-7x+2) ÷ (x-1)

Show that x+4 is a factor of x³ + 6x² - 7x - 60

Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent:

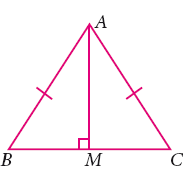
In the figure find x⁰ and y⁰.

Write the coordinates of quadrilateral PQRS as shown in the following figure.

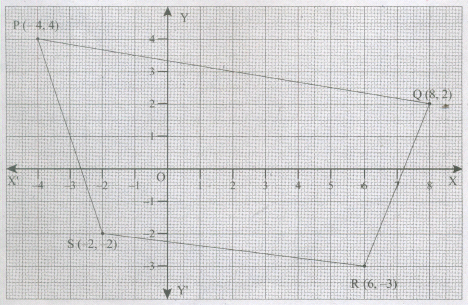
The point (3, −4) is the centre of a circle. If AB is a diameter of the circle and B is (5, −6), find the coordinates of A.

The average mark of 25 students was found to be 78.4. Later on, it was found that score of 96 was misread as 69. Find the correct mean of the marks

The following table represents the marks obtained by a group of 12 students in a class test in Mathematics and Science

Marks (Mathematics)	52	55	32	30	60	44	28	25	50	75	33	62
Marks (Science)	54	42	48	49	27	25	24	19	28	58	42	69

Indicate in which subject, the level of achievement is higher?

Express
(i) sin 74° in terms of cosine
(ii) tan 12° in terms of cotangent
(iii) cosec 39° in terms of secant

Find the TSA and LSA of a cuboid whose length, breadth and height are 7.5 m, 3 m and 5 m respectively.

In an office, where 42 staff members work, 7 staff members use cars, 20 staff members use two-wheelers and the remaining 15 staff members use cycles. Find the relative frequencies.

If A =\(\left\{ \cfrac { 1 }{ 2 } ,1\cfrac { 5 }{ 4 } ,\cfrac { 7 }{ 4 } ,3 \right\} \) ,B =\(\left\{ 1\cfrac { 5 }{ 4 } ,\cfrac { 7 }{ 4 } ,3\cfrac { 7 }{ 2 } \right\} \) Now and C =\(\left\{ \cfrac { 1 }{ 2 } ,\cfrac { 5 }{ 4 } ,2,3\cfrac { 7 }{ 2 } \right\} \), then verify \(A\cap \left( B\cap C \right) \)= \(\left( A\cap B \right) \cap C\)

Find any  seven rational numbers between \(\frac { 5 }{ 8 } \) and \(\frac { 5 }{ 6 } \)

Represent \(-\frac { 2 }{ 11 } ,-\frac { 5 }{ 11 } and-\frac { 9 }{ 11 } \)on the number line.

Prove that x -1 is a factor x⁵ - 45x⁴ + 36x³ + 45x² - 36x^-1

Find the angle of the given cyclic quadrilateral ABCD in the figure.

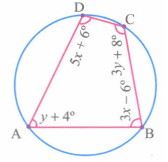
Construct the centroid of \(\triangle\)PQR such that PQ = 9 cm, PQ = 7cm, RP = 8 cm.

Find x such that PQ = QR where P(6, -1) Q (1, 3) and R (x, 8) respectively.

Find the Arithmetic Mean of the following data using Step Deviation Method

Age	15-19	20-24	25-29	30-34	35-39	40-44
No.of persons	4	20	38	24	10	9

Find the area of a quadrilateral ABCD whose sides are AB = 8cm, BC = 15 cm, CD = 12 cm, AD = 25 cm and = 90°.