- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Chemistry
-

Physics
-

Maths
-

Accountancy
-

Business Studies
-

Economics
-

Introductory Micro and Macroeconomics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Political Science
-

Engineering Graphics
-

Bio Technology
-

Entrepreneurship
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Psychology
-

Hindi Core
-

Tamil
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Physics
-

Mathematics
-

Chemistry
-

Biology
-

Economics
-

Business Studies
-

Accountancy
-

Computer Science
-

English
-

Geography
-

History
-

Physical Education
-

Psychology
-

Sociology
-

Bio Technology
-

Enterprenership
-

Hindi
-

Home Science
-

Political Science
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Social Science
-

Mathematics
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

9th Standard Mathematics Annual model Question Bank Software Feb-11 , 2020
9th Standard Mathematics Annual model
-
If B ⊆ A then n(A∩B) is –––––––––.
(a)n(A – B)
(b)n(B)
(c)n(B – A)
(d)n(A)
-
If A is a proper subset of B, then A ∩ B = __________
(a)A
(b)B
(c)Ø
(d)A U B
-
What is 5.92 \(\times\)10-3 written in decimal form?
(a)0.000592
(b)0.00592
(c)0.0592
(d)0.592
-
The length of a square is 1.2\(\times\)103 m. Its area is_______
(a)14.4 \(\times\) 106
(b)1.44 \(\times\) 106
(c)0.144 \(\times\) 10
(d)1440
-
The zero of the polynomial 2x+5 is _______.
(a)\(\frac {5}{2}\)
(b)\(-\frac {5}{2}\)
(c)\(\frac {2}{5}\)
(d)\(-\frac {2}{5}\)
-
If x - 2 is a factor of q(x), then the remainder is___________
(a)q(-2)
(b)x - 2
(c)0
(d)-2
-
The angle in a semi circle is_________
(a)180°
(b)90°
(c)60°
(d)45°
-
If Q1, Q2, Q3, Q4 are the quadrants in a Cartesian plane then \({ Q }_{ 2 }\cap { Q }_{ 3 }\) is ______.
(a)\({ Q }_{ 1 }\cup { Q }_{ 2 }\)
(b)\({ Q }_{ 2 }\cup { Q }_{ 3 }\)
(c)Null set
(d)Negative x-axis
-
The point whose abscissa is 5 and lies on the x-axis is__________
(a)(-5, 0)
(b)(5,5)
(c)(0,5)
(d)(5,0)
-
The mean of a, b, c, d and e is 28. If the mean of a, c and e is 24, then mean of b and d is _______.
(a)24
(b)36
(c)26
(d)34
-
The mean of the first 10 whole number is
(a)4
(b)4.5
(c)5
(d)5.5
-
The value of 3 sin 700sec 200 + 2 sin 490sec 510 is ________.
(a)2
(b)3
(c)5
(d)6
-
The number of bricks each measuring 50 cm × 30 cm × 20 cm that will be required to build a wall whose dimensions are 5 m × 3 m × 2 m is _______.
(a)1000
(b)2000
(c)3000
(d)5000
-
A letter is chosen at random from the word “STATISTICS”. The probability of getting a vowel is
(a)\(\frac { 1 }{ 10 } \)
(b)\(\frac { 2 }{ 10 } \)
(c)\(\frac { 3 }{ 10 } \)
(d)\(\frac { 4 }{ 10 } \)
-
Which of the following sets are equivalent or unequal or equal sets?
G = {x : x is a prime number and 3 < x < 23}
H = {x : x is a divisor of 18} -
Express the following in the form 3n: \(\sqrt { 27 } \)
-
Find whether x and y are rational or irrational in the following
(i) a = 2 + \(\sqrt { 3 } \) , b = 2 - \(\sqrt { 3 } \) ; x = a + b, y = a+ b
(ii) a = \(\sqrt { 2 } \) + 7, b = \(\sqrt { 2 } \) - 7 ; x = a + b, y = a - b
(iii) a = \(\sqrt { 75 } \), b = \(\sqrt { 3 } \), x = ab, y = \(\frac { a }{ b } \)
(iv) a = \(\sqrt { 18 } \), b = \(\sqrt { 3 } \), x = ab, y = \(\frac { a }{ b } \) -
Find any 3 irrational numbers between 0.12 and 0.13.
-
Expand the following: (2a-3b+4c)2
-
Draw the circumcircle for, An isosceles right triangle having 6 cm as the length of the equal sides.
-
The points A(−5, 4) , B(−1, −2) and C(5,2) are the vertices of an isosceles rightangled triangle where the right angle is at B. Find the coordinates of D so that ABCD is a square.
-
If A (10, 11) and B (2 ,3) are the coordinates of end points of diameter of circle. Then find the centre of the circle.
-
Find the coordinates of the point which divides, the line segment joining the point A (3,7) and B (-11, -2) in the ratio 5 : 1.
-
A set of numbers consists of five 4’s, four 5’s, nine 6’s,and six 9’s. What is the mode.
-
From the given figure, find all the trigonometric ratios of angle \(\theta\).
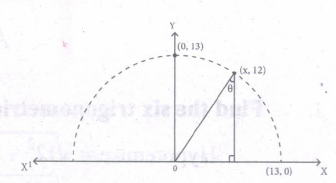
-
Find the value of \(\frac{\tan 25^{\circ}}{\cot 65^{\circ}}+\frac{\sin 40^{\circ}}{\cos 50^{\circ}}\)
-
Find the surface area of a cube whose edge is
(i) 27 cm
(ii) 3 cm
(iii) 6 cm
(iv) 2.1 cm -
Two dice are rolled, find the probability that the sum is
(i) equal to 1
(ii) equal to 4
(iii) less than 13

-
Given that A = {1,3,5,7} B = {1,2,4,6,8}. Find
(i) AΔB and
(ii) BΔA -
Verify \(\left( A\cup B \right) '\)=\(A'\cap B'\) using Venn diagrams
-
Express the following decimal expression into rational numbers \(0.\overline { 0001 } \)
-
Locate an irrational number between two rational numbers\(\frac { 23 }{ 10 } \) and\(\frac { 12 }{ 5 } \)
-
Add \(\sqrt [ 5 ]{ 11 } \) and \(\sqrt [ 7 ]{ 11 } \). Check whether the sum is rational or irrational
-
What must added to \({ x }^{ 4 }-3x^{ 2 }+2x+6\quad to\quad get\quad { x }^{ 4 }-2x^{ 3 }-x+8?\)
-
Check the value of k for which the given system of equations kx + 2y = 3; 2x − 3y = 1 has a unique solution.
-
In the figure, AB is parallel to CD, find x
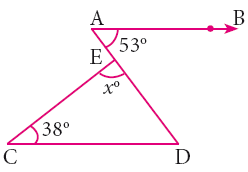
-
Find the perimeter of the triangle whose vertices are(3, 2), (7, 2) and (7, 5).
-
The point (3, −4) is the centre of a circle. If AB is a diameter of the circle and B is (5, −6), find the coordinates of A.
-
Find the median of the given values: 47, 53, 62, 71, 83, 21, 43, 47, 41
-
Find the value of sin 64034'.
-
Find the TSA and LSA of a cuboid whose length, breadth and height are 7.5 m, 3 m and 5 m respectively.
-
When a dice is rolled, find the probability to get the number greater than 4?
-
Find the quotient and remainder for the following using synthetic division:
(i) (x3+x2-7x-3) ÷ (x - 3)
(ii) (x3+2x2-x-4) ÷ (x + 2)
(ii) (3x3-2x2+7x-5) ÷ (x + 3)
(iv) (8x4-2x2+6x+5) ÷ (4x + 1) -
Factorise 2x3- x2 - 12x - 9 into linear factors
-
Construct an isosceles triangle ABC with AB = BC of sides 7 cm and ㄥB = 700 and locate its Orthocentre.
-
Draw an equilateral triangle of side 8 cm and locate its incentre. Also draw the incircle.
Part I
Answer all the questions.
Choose the most suitable answer from the given four alternatives and write the option code with the corresponding answer.
14 x 1 = 14
Part II
Answer any 10 questions. Question no. 28 is compulsory.
14 x 2 = 28
Part III
Answer any 10 questions. Question no. 42 is compulsory.
14 x 3 = 42
Part IV
Answer all the questions
4 x 5 = 20






 9th Standard Maths Syllabus
9th Standard Maths Syllabus  9th Standard Maths Study Materials
9th Standard Maths Study Materials

Reviews & Comments about 9th Standard Mathematics Annual model
Write your Comment