Give any two examples for linear equations in one variable.

Two cars are 100 miles apart. If they drive towards each other they will meet in 1 hour. If they drive in the same direction they will meet in 2 hours. Find their speed by using graphical method.

Raman’s age is three times the sum of the ages of his two sons. After 5 years his age will be twice the sum of the ages of his two sons. Find the age of Raman.

The monthly income of A and B are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves Rs. 5,000 per month, find the monthly income of each.

It takes 24 hours to fill a swimming pool using two pipes. If the pipe of larger diameter is used for 8 hours and the pipe of the smaller diameter is used for 18 hours. Only half of the pool is filled. How long would each pipe take to fill the swimming pool.

The sum of the numerator and denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(\frac { 1 }{ 2 } \). Find the fraction.

Points A and B are 70 km apart on a highway. A car starts from A and another car starts from B simultaneously. If they travel in the same direction, they meet in 7 hours, but if they travel towards each other, they meet in one hour. Find the speed of the two cars.

On selling a T.V. at 5% gain and a fridge at 10% gain, a shopkeeper gains Rs. 2000. But if he sells the T.V. at 10% gain and the fridge at 5% loss, he gains Rs. 1500 on the transaction. Find the actual price of the T.V. and the fridge.

Two numbers are in the ratio 5:6. If 8 is subtracted from each of the numbers, the ratio becomes 4:5. Find the numbers.

A railway half ticket costs half the full fare and the reservation charge is the same on half ticket as on full ticket. One reserved first class ticket from Mumbai to Ahmadabad costs Rs. 216 and one full and one half reserved first class ticket costs Rs. 327. What is the basic first class full fare and what is the reservation charge?

Find the slopes of all the lines from the adjacent figure,

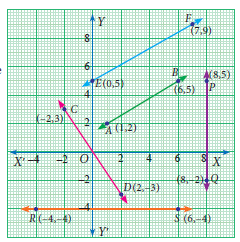
(Computing slope made easier!) Find the slope and y-intercept of the line given by the equation 2y – 3x = 12.

Check whether (5, −1) is a solution of the simultaneous equations x – 2y = 7 and 2x + 3y = 7.

Solve the system of linear equations x + 3y = 16 and 2x − y = 4 by substitution method.

Given 4a + 3b = 65 and a + 2b = 35 solve by elimination method.

Solve 2x + 3y = 14 and 3x − 4y = 4 by the method of elimination.

Solve by cross multiplication method : 3x + 5y = 21; −7x − 6y = −49

Check the value of k for which the given system of equations kx + 2y = 3; 2x − 3y = 1 has a unique solution.

Find the value of k, for the following system of equation has infinitely many solutions. 2x − 3y = 7;(k + 2)x − (2k +1)y = 3(2k −1)

Find the value of k for which the system of linear equations 8x + 5y = 9; kx +10y = 15 has no solution.

(Graphing made easier!) Draw the graph of the line given by the equation y = 4x – 3.

Use graphical method to solve the following system of equations x + y = 5; 2x – y = 4.

Use graphical method to solve the following system of equations 3x + 2y = 6; 6x + 4y = 8

The perimeter of a rectangle is 36 metres and the length is 2 metres more than three times the width. Find the dimension of rectangle by using the method of graph.

The sum of the digits of a given two digit number is 5. If the digits are reversed, the new number is reduced by 27. Find the given number.

Solve for x and y: 8x − 3y = 5xy, 6x − 5y = −2xy by the method of elimination.

Solve 3x − 4y = 10 and 4x + 3y = 5 by the method of cross multiplication.

Check whether the following system of equation is consistent or inconsistent and say how many solutions we can have if it is consistent.
(i) 2x – 4y = 7
x – 3y = –2
(ii) 4x + y = 3
8x + 2y = 6
(iii) 4x +7 = 2 y
2x + 9 = y