If A = {x, y, z} then the number of non - empty subsets of A is ________.

(a)

8

(b)

5

(c)

6

(d)

7

Which of the following is correct?

(a)

∅ ⊆ {a, b}

(b)

∅ ∈ {a, b}

(c)

{a} ∈ {a, b}

(d)

a ⊆ {a, b}

If A∪B = A∩B, then ________.

(a)

A ≠ B

(b)

A = B

(c)

A ⊂ B

(d)

B ⊂ A

If B - A is B, then A∩B is ________.

(a)

A

(b)

B

(c)

U

(d)

∅

The shaded region in the adjacent diagram represents ______________

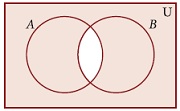(a)

(A∪B)′

(b)

(A∩B)′

(c)

A′∩B′

(d)

A∩B

From the adjacent diagram n[P(AΔB)] is ________.

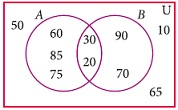(a)

8

(b)

16

(c)

32

(d)

64

If n(A) = 10 and n(B) = 15, then the minimum and maximum number of elements in A ∩ B is ________.

(a)

(10,15)

(b)

(15,10)

(c)

(10,0)

(d)

(0,10)

If X = {x : x = 4(n – 1), n ∈ N} and Y = {y : y = 3n – 2n – 1, n ∈ N}, then X∪Y is ______________

(a)

W

(b)

X

(c)

Y

(d)

N

Let A = {∅} and B = P(A), then A∩B is ________.

(a)

{ ∅, {∅} }

(b)

{∅}

(c)

∅

(d)

{0}

In a class of 50 boys, 35 boys play Carrom and 20 boys play Chess then the number of boys play both games is________.

(a)

5

(b)

30

(c)

15

(d)

10

If n is a natural number then \(\sqrt { n } \) is ________.

(a)

always a natural number

(b)

always an irrational number

(c)

always a rational number

(d)

may be rational or irrational

Which of the following is not true?

(a)

Every rational number is a real number

(b)

Every integer is a rational number

(c)

Every real number is an irrational number

(d)

Every natural number is a whole number

Which one of the following, regarding sum of two irrational numbers, is true?

(a)

always an irrational number

(b)

may be a rational or irrational number

(c)

always a rational number

(d)

always an integer.

Which one of the following has a terminating decimal expansion?

(a)

\(\frac { 5 }{ 64 } \)

(b)

\(\frac { 8 }{ 9 } \)

(c)

\(\frac { 14 }{ 15 } \)

(d)

\(\frac { 1 }{ 12 } \)

Which one of the following is an irrational number.

(a)

\(\sqrt { 25 } \)

(b)

\(\sqrt { \frac { 9 }{ 4 } } \)

(c)

\(\frac { 7 }{ 11 } \)

(d)

\(\pi\)

An irrational number between 2 and 2.5 is ________.

(a)

\(\sqrt { 11 } \)

(b)

\(\sqrt { 5 } \)

(c)

\(\sqrt { 2.5 } \)

(d)

\(\sqrt { 8 } \)

The smallest rational number by which \(\frac { 1 }{ 3 } \)  should be multiplied so that its decimal expansion terminates after one place of decimal is   ________.

(a)

\(\frac { 1 }{ 10 } \)

(b)

\(\frac { 3 }{ 10 } \)

(c)

3

(d)

30

The number \(0.\bar { 3 } \) in the form \(\frac { p }{ q } \) where p and q are integers and \(q\neq 0\)

(a)

\(\frac { 33 }{ 100 } \)

(b)

\(\frac { 3 }{ 10 } \)

(c)

\(\frac { 1 }{ 3 } \)

(d)

\(\frac { 3 }{ 100 } \)

The value of  \(0.\bar { 23 } +0.\bar { 22 } \) is ____________

(a)

\(0.\bar { 43 } \)

(b)

0.45

(c)

\(0.4\bar { 5 } \)

(d)

\(0.\bar { 45 } \)

if \(\frac { 1 }{ 7 } \) = \(0.\overline { 142857 } \) then the value of \(\frac { 5 }{ 7 } \) ________.

(a)

\(0.\overline { 142857 } \)

(b)

\(0.\overline { 714285 } \)

(c)

\(0.\overline { 571428 } \)

(d)

0.714285

Find the odd one out of the following.

(a)

\(\sqrt { 32 } \times \sqrt { 2 } \)

(b)

\(\frac { \sqrt { 27 } }{ \sqrt { 3 } } \)

(c)

\(\sqrt { 72 } \times \sqrt { 8 } \)

(d)

\(\frac { \sqrt { 54 } }{ \sqrt { 18 } } \)

\(0.\overline { 34 } +0.3\bar { 4 } \) = ________.

(a)

\(0.6\overline { 87 } \)

(b)

\(0.\overline { 68 } \)

(c)

\(0.6\bar { 8 } \)

(d)

\(0.68\bar { 7 } \)

If x³ + 6x² + kx + 6 is exactly divisible by (x + 2), then k= ?

(a)

-6

(b)

-7

(c)

-8

(d)

11

The root of the polynomial equation 2x + 3 = 0 is ________.

(a)

\(\frac{1}{3}\)

(b)

\(-\frac{1}{3}\)

(c)

\(-\frac{3}{2}\)

(d)

\(-\frac{2}{3}\)

The type of the polynomial 4–3x³ is  ________.

(a)

constant polynomial

(b)

linear polynomial

(c)

quadratic polynomial

(d)

cubic polynomial.

x³ – x² is a …………..

(a)

monomial

(b)

binomial

(c)

trinomial

(d)

constant polynomial

If x⁵¹ + 51 is divided by x + 1, then the remainder is _______.

(a)

0

(b)

1

(c)

49

(d)

50

The zero of the polynomial 2x+5 is _______.

(a)

\(\frac {5}{2}\)

(b)

\(-\frac {5}{2}\)

(c)

\(\frac {2}{5}\)

(d)

\(-\frac {2}{5}\)

The sum of the polynomials p(x) = x³ – x² – 2, q(x) = x²–3x+ 1 _______.

(a)

x³ – 3x – 1

(b)

x³ + 2x² – 1

(c)

x³ – 2x² – 3x

(d)

x³ – 2x² + 3x –1

The product of the polynomials p(x) = 4x –3 q(x) = 4x + 3 ____________

(a)

1 – x – 8

(b)

16x² – 9

(c)

18x³ + 12x² – 12x – 8

(d)

18x³ – 12x² + 12x + 8

The remainder when p(x) = x³ – ax² + 6x – a is divided by (x – a) is ______________

(a)

–5a

(b)

\(\frac {1}{5}\)

(c)

5

(d)

5a

The Auto fare is found as minimum Rs. 25 for 3 kilometer and thereafter Rs. 12 for per kilometer. Which of the following equations represents the relationship between the total cost ‘c’ in rupees and the number of kilometers n?

(a)

c = 25 + n

(b)

c = 25 + 12n

(c)

c = 25 + (n–3)12

(d)

c = (n–3)12

Degree of the polynomial (y³–2)(y³ + 1) is _______.

(a)

9

(b)

2

(c)

3

(d)

6

Let the polynomials be
(A) –13q⁵ + 4q² + 12q
(B) (x² +4 )(x² + 9)
(C) 4q⁸ – q⁶ + 2
(D) -\(\frac {5}{7}\)y¹²+y³+y⁵
Then ascending order of their degree is _______.

(a)

A,B,D,C

(b)

A,B,C,D

(c)

B,C,D,A

(d)

B,A,C,D

It is not possible to construct a triangle when its sides are ____________

(a)

8.2 cm, 3.5 cm, 6.5 cm

(b)

6.3 cm, 3.1 cm, 3.2 cm

(c)

7 cm, 8 cm, 10 cm

(d)

4 cm, 6 cm, 6 cm

The exterior angle of a triangle is equal to the sum of two ________.

(a)

Exterior angles

(b)

Interior opposite angles

(c)

Alternate angles

(d)

Interior angles

In the quadrilateral ABCD, AB = BC and AD = DC Measure of ∠BCD is ________.

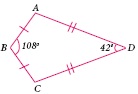(a)

150°

(b)

30°

(c)

105°

(d)

72°

ABCD is a square, diagonals AC and BD meet at O. The number of pairs of congruent triangles with vertex O are ________.

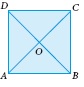(a)

6

(b)

8

(c)

4

(d)

12

In the given figure CE || DB then the value of x⁰ is  ________.

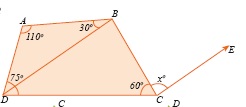(a)

45°

(b)

30°

(c)

75°

(d)

85°

The correct statement out of the following is ________.

(a)

ΔABC ≅ ΔDEF

(b)

ΔABC ≅ ΔDEF

(c)

ΔABC ≅ ΔFDE

(d)

ΔABC ≅ ΔFED

If the diagonal of a rhombus are equal, then the rhombus is a ________.

(a)

Parallelogram but not a rectangle

(b)

Rectangle but not a square

(c)

Square

(d)

Parallelogram but not a square

If bisectors of ∠A and ∠B of a quadrilateral ABCD meet at O, then ∠AOB is ________.

(a)

∠C + ∠D

(b)

\(\frac { 1 }{ 2 } (\angle C+\angle D)\)

(c)

\(\frac { 1 }{ 2 } \angle C+\frac { 1 }{ 3 } \angle D\)

(d)

\(\frac { 1 }{ 3 } \angle C+\frac { 1 }{ 2 } \angle D\).

The interior angle made by the side in a parallelogram is 90° then the parallelogram is a ________.

(a)

rhombus

(b)

rectangle

(c)

trapezium

(d)

kite

Which of the following statement is correct?

(a)

Opposite angles of a parallelogram are not equal.

(b)

Adjacent angles of a parallelogram are complementary.

(c)

Diagonals of a parallelogram are always equal.

(d)

Both pairs of opposite sides of a parallelogram are always equal.

The angles of the triangle are 3x–40, x+20 and 2x–10 then the value of x is ________.

(a)

40°

(b)

35°

(c)

50°

(d)

45°

Point (–3, 5) lie in the ________ quadrant

(a)

I

(b)

II 

(c)

III 

(d)

IV 

Signs of the abscissa and ordinate of a point in the fourth quadrant are respectively

(a)

(+,+)

(b)

( –, –)

(c)

(–, +)

(d)

( +, –)

Point (0, –7) lies ________

(a)

on the x-axis

(b)

in the II quadrant

(c)

on the y-axis

(d)

in the IV quadrant

Point (–10, 0) lies ___________

(a)

on the negative direction of x-axis

(b)

on the negative direction of y-axis

(c)

in the III quadrant

(d)

in the IV quadrant

If the y-coordinate of a point is zero, then the point always lies ______.

(a)

in the I quadrant

(b)

in the II quadrant

(c)

on x-axis

(d)

on y-axis

The point M lies in the IV quadrant. The coordinates of M is _______

(a)

(a,b)

(b)

(–a, b)

(c)

(a, –b)

(d)

(–a, –b)

The points (–5, 2) and (2, –5) lie in the ________.

(a)

same quadrant

(b)

II and III quadrant respectively

(c)

II and IV quadrant respectively

(d)

IV and II quadrant respectively

On plotting the points O(0, 0), A(3, – 4), B(3, 4) and C(0, 4) and joining OA, AB, BC and CO, which of the following figure is obtained?

(a)

Square

(b)

Rectangle

(c)

Trapezium

(d)

Rhombus

If P( –1, 1), Q( 3, -4), R( 1,  -1), S(-2, -3) and T( -4, 4) are plotted on a graph paper, then the points in the fourth quadrant are ______.

(a)

P and T

(b)

Q and R

(c)

only S

(d)

P and Q

The point whose ordinate is 4 and which lies on the y-axis is ______.

(a)

( 4, 0 )

(b)

(0, 4)

(c)

(1, 4)

(d)

(4, 2)

The distance between the two points ( 2, 3 ) and ( 1, 4 ) is ______.

(a)

2

(b)

\(\sqrt { 56 } \)

(c)

\(\sqrt { 10 } \)

(d)

\(\sqrt { 2 } \)

If the points A (2, 0), B (-6, 0), C (3, a-3) lie on the x-axis then the value of a is _____.

(a)

0

(b)

2

(c)

3

(d)

-6

If ( x+2, 4) = (5, y–2), then the coordinates (x,y) are _____.

(a)

(7, 12)

(b)

(6, 3)

(c)

(3, 6)

(d)

(2, 1)

If Q₁, Q₂, Q₃, Q₄ are the quadrants in a Cartesian plane then \({ Q }_{ 2 }\cap { Q }_{ 3 }\) is ______.

(a)

\({ Q }_{ 1 }\cup { Q }_{ 2 }\)

(b)

\({ Q }_{ 2 }\cup { Q }_{ 3 }\)

(c)

Null set

(d)

Negative x-axis

The distance between the point ( 5, –1 ) and the origin is _______.

(a)

\(\sqrt { 24 } \)

(b)

\(\sqrt { 37 } \)

(c)

\(\sqrt { 26 } \)

(d)

\(\sqrt { 17 } \)