- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Chemistry
-

Physics
-

Maths
-

Accountancy
-

Business Studies
-

Economics
-

Introductory Micro and Macroeconomics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Political Science
-

Engineering Graphics
-

Bio Technology
-

Entrepreneurship
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Psychology
-

Hindi Core
-

Tamil
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Physics
-

Mathematics
-

Chemistry
-

Biology
-

Economics
-

Business Studies
-

Accountancy
-

Computer Science
-

English
-

Geography
-

History
-

Physical Education
-

Psychology
-

Sociology
-

Bio Technology
-

Enterprenership
-

Hindi
-

Home Science
-

Political Science
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Social Science
-

Mathematics
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Social Science
-

Science
-

Mathematics
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students
11th Standard கணிதம் - வகை நுண்கணிதம் எல்லைகள் மற்றும் தொடர்ச்சித் தன்மை மாதிரி கொஸ்டின் பேப்பர் ( 11th Standard Maths - Differential Calculus - Limits and Continuity Model Question Paper ) Vinothan - Rameswaram Nov-06 , 2019
வகை நுண்கணிதம் எல்லைகள் மற்றும் தொடர்ச்சித் தன்மை
வகை நுண்கணிதம் எல்லைகள் மற்றும் தொடர்ச்சித் தன்மை மாதிரி கொஸ்டின் பேப்பர்
11th Standard
-
Reg.No. :
கணிதம்
Time :
02:00:00 Hrs
Total Marks :
60
-
சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்.
\(\lim _{ x\rightarrow \infty }{ \frac { \sin { x } }{ x } } \) ______.(a)1
(b)0
(c)\(\infty \)
(d)\(-\infty \)
-
சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்
\(\lim _{ x\rightarrow \infty }{ \left( \frac { { x }^{ 2 }+5x+3 }{ { x }^{ 2 }+x+3 } \right) } ^{ x }\) ______.(a)\({ e }^{ 4 }\)
(b)\({ e }^{ 2 }\)
(c)\({ e }^{ 3 }\)
(d)1
-
சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்.
\(\lim _{ x\rightarrow \infty }{ \frac { { a }^{ x }-{ b }^{ x } }{ x } } =\) ______.(a)\(\log { ab } \)
(b)\(\log { \left( \frac { a }{ b } \right) } \)
(c)\(\log { \left( \frac { b }{a } \right) } \)
(d)\(\frac { a }{ b } \)
-
சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்.
\(f(x)=x(-1{ ) }^{ \left\lfloor \frac { 1 }{ x } \right\rfloor },\ x\le 0,\) இங்கு x என்பது x-க்குச் சமமான அல்லது குறைவான மீப்பெரு முழு எண், எனில், \(\lim _{ x\rightarrow 0 }{ f(x) } \)-ன் மதிப்பு ______.(a)-1
(b)0
(c)2
(d)4
-
சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்.
\(\lim _{ x\rightarrow 3 }{ \left\lfloor x \right\rfloor } =\) ______.(a)2
(b)3
(c)மதிப்பு இல்லை
(d)0
-
சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்
\(\lim _{ x\rightarrow 0 }{ \frac { { xe }^{ x }-\sin { x } }{ x } } \)-ன் மதிப்பு ______.(a)1
(b)2
(c)3
(d)0
-
சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்.
\(\lim _{ x\rightarrow 0 }{ \frac { { e }^{ \sin { x } }-1 }{ x } } =\)______.(a)1
(b)e
(c)\(\frac { 1 }{ e } \)
(d)0
-
சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்.\(x=\frac { 3 }{ 2 } \)-ல் \(f(x)=\frac { \left\lfloor 2x-3 \right\rfloor }{ 2x-3 } \)என்பது ______.
(a)தொடர்ச்சியானது
(b)தொடர்ச்சியற்றது
(c)வகையிடத்தக்கது
(d)புஜ்ஜியமற்றது
-
சரியான அல்லது மிகவும் ஏற்புடைய விடையினைக் கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து தேர்ந்தெடுக்கவும்
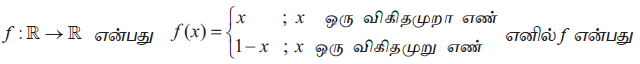 ______.(a)
______.(a)\(x=\frac { 1 }{ 2 } \)-ல் தொடர்ச்சியற்றது
(b)\(x=\frac { 1 }{ 2 } \)-ல் தொடர்ச்சியானது
(c)எல்லா இடங்களிலும் தொடர்ச்சியானது
(d)எல்லா இடங்களிலும் தொடர்ச்சியற்றது
-
பின்வருவனவற்றுள் பொருந்தாத ஒன்றை தேர்வு செய்க.
(a)sin x=2
(b)ex=-2
(c)tan x=7
(d)|x|=-1
-
1 முதல் 6 வரை உள்ள கணக்குகளுக்குக் அட்டவணையைப் பயன்படுத்தி எல்லை மதிப்பைக் கணக்கிடுக.
\(\lim _{ x\rightarrow 2 }{ \frac { x-2 }{ { x }^{ 2 }-x-2 } } \)x 1.9 1.99 1.999 2.001 2.01 2.1 f(x) 0.344820 0.33444 0.33344 0.333222 0.33222 0.332258 -
1 முதல் 6 வரை உள்ள கணக்குகளுக்குக் அட்டவணையைப் பயன்படுத்தி எல்லை மதிப்பைக் கணக்கிடுக.
\(\lim _{ x\rightarrow 0 }{ \frac { \sin { x } }{ x } } \)x -0.1 -0.01 -0.001 0.001 0.01 0.1 f(x) 0.99833 0.99998 0.99999 0.99999 0.99998 0.99833 -
பின்வரும் கணக்குகளுக்கு வரைபடத்தைப் பயன்படுத்தி எல்லை மதிப்பைக் காண்க(உள்ளது எனில்). எல்லை மதிப்பு இல்லை எனில், காரணத்தை விளக்குக.
\(\lim _{ x\rightarrow 1 }{ ({ x }^{ 2 }+2) } \)
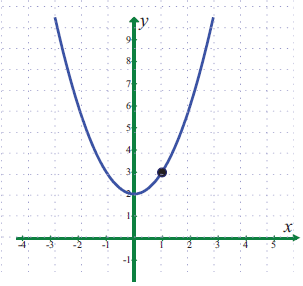
-
பின்வரும் கணக்குகளுக்கு வரைபடத்தைப் பயன்படுத்தி எல்லை மதிப்பைக் காண்க(உள்ளது எனில்). எல்லை மதிப்பு இல்லை எனில், காரணத்தை விளக்குக.
\(\lim _{ x\rightarrow 1 }{ f(x) } .\) இங்கு \(f(x)=\begin{cases} { x }^{ 2 }+2,\quad x\neq 1 \\ 1,\quad \quad x=1 \end{cases}\)
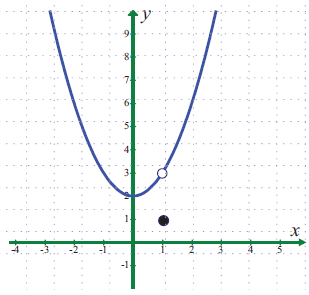
-
\(\lim _{ x\rightarrow 3 }{ ({ x }^{ 3 }-2x+6)- } \) ன் மதிப்பைக் கணக்கிடுக.
-
கணக்கிடுக :\(\lim _{ x\rightarrow 1 }{ \frac { \sqrt { x } -1 }{ x-1 } } \)
-
\(\lim _{ x\rightarrow 3 }{ \frac { { x }^{ 3 }-{ 3 }^{ n } }{ x-3 } = } 27\) எனுமாறு உள்ள மிகை முழு எண் n-ஐ காண்க.
-
எல்லையின் மதிப்பைக் காண்க :\(\lim _{ x\rightarrow \infty }{ \frac { { x }^{ 3 }+x }{ { { x }^{ 4 }-3x }^{ 2 }+1 } } \)
-
பின்வருவனவற்றின் மதிப்பைக் காண்க:\(\lim _{ x\rightarrow \infty }{ { \left( 1+\frac { 1 }{ x } \right) }^{ 7x } } \)
-
பின்வருவனவற்றின் மதிப்பைக் காண்க:\(\lim _{ x\rightarrow 0 }{ { \frac { \sin ^{ 3 }{ \left( \frac { x }{ 2 } \right) } }{ { x }^{ 3 } } } } \)
-
f(x) = 2x2 + 3x - 5 R- ன் எல்லா புள்ளிகளிலும் தொடர்ச்சியானது என நிறுவுக.
-
\(\lim _{ x\rightarrow 0 }{ \left| x \right| } \) -ன் மதிப்பு காண்க.
-
\(f(x)=\begin{cases} \frac { \left| x+5 \right| }{ x+5 } ,;\quad x\neq -5 \\ 0,\ ;\quad x=-5 \end{cases}\) எனில் \(\lim _{ x\rightarrow -5 }{ f(x) } \) கிடைக்கப் பெறுமா எனச் சோதிக்க.
-
கணக்கிடுக: \(\lim _{ x\rightarrow -1 }{ ({ x }^{ 2 }-3) } ^{ 10 }.\)
-
பின்வரும் எல்லை மதிப்பினைக் காண்க: \(\lim _{ x\rightarrow 5 }{ \frac { \sqrt { x+4 } -3 }{ x-5 } } \)
-
ஒரு தொட்டியில் 5000 லிட்டர் நல்ல நீர் உள்ளது என்க. ஒரு லிட்டருக்கு 30 கி அளவு உப்பு கொண்ட உவர் நீர் 25 லி/நிமிடம் என்ற அளவில் தொட்டியில் செலுத்தப்படுகின்றது. t நிமிடங்களில் இந்த உவர் நீரின் அடர்த்தி (கிராம்/லிட்டர்)\(C(t)=\frac { 30t }{ 200+t } \) என தரப்பட்டுள்ளது.\(t\rightarrow \infty \) எனில் அடர்த்தி எவ்வாறு மாறும்?
-
\(f(x)=x\sin { \frac { \pi }{ x } } \) என்க. \(f(0)\)-ன் எந்த மதிப்புக்கு f எல்லா இடங்களிலும் தொடர்ச்சியானதாக இருக்கும்?
-
\(\lim _{ x\rightarrow { 0 }^{ + } }{ x\left[ \left\lfloor \frac { 1 }{ x } \right\rfloor +\left\lfloor \frac { 2 }{ x } \right\rfloor +...+\left\lfloor \frac { 15 }{ x } \right\rfloor \right] } =120\) என நிறுவுக.
-
\(g(x)=\begin{cases} { x }^{ 2 }-{ b }^{ 2 };\quad x<4 \\ bx+20;\quad x\ge 4 \end{cases}\) என்ற சார்பு \((-\infty ,\infty )\)-ல் தொடர்ச்சியானது எனில் மாறிலி b-ஐக் காண்க.
10 x 1 = 10
11 x 2 = 22
6 x 3 = 18
2 x 5 = 10






 11th Standard Maths Syllabus
11th Standard Maths Syllabus  11th Standard Maths MCQ Practise Tests
11th Standard Maths MCQ Practise Tests 

Reviews & Comments about 11th Standard கணிதம் - வகை நுண்கணிதம் எல்லைகள் மற்றும் தொடர்ச்சித் தன்மை மாதிரி கொஸ்டின் பேப்பர் ( 11th Standard Maths - Differential Calculus - Limits and Continuity Model Question Paper )
Write your Comment