கீழ்க்காணும் தொடர்புகளுக்கு தற்சுட்டு, சமச்சீர் மற்றும் கடப்பு ஆகியவற்றை பற்றி ஆராய்க.
மிகை முழு எண்களில் தொடர்பு R ஆனது “n -ன் வகுத்தி m ஆக இருந்தால் mRn” என வரையறுக்கப்படுகிறது.

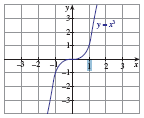
கொடுக்கப்பட்டுள்ள y= x³ என்ற வளைவரையின் படத்தினைப் பயன்படுத்தி அச்சு மதிப்பு மாறாமல் ஒரே தளத்தில் கீழ்க்கா்க்காணும் சார்புகளை வரைக.
1. y=-x³
2. y=x³+1
3. y=x³-1
4. y=(x+1)³

y = x என்ற நேர்கோட்டின் மூலம்
1. y = -x
2. y = 2x
3. y = x +1
4.\(y={1\over2}x+1\)
5.2x + y + 3 = 0 ஆகியவற்றைத் தோராயமாக வரைக.

f : [-2, 2] ⟶ B என்ற சார்பு f(x)-2x³, என வரையறுக்கப்படுகிறது எனில் f ஒரு மேற்கோர்த்தலாக அமைய B –ஐக் காண்க

\(f(x)={1\over 1-3\cos x}\) - ன் வீச்சகம் காண்க.

தீர்வு காண்க
(i) \(\frac{3(x-2)}{5}\le\frac{5(2-x)}{3}\)
(ii) ​\(\frac{5-x}{3}<\frac{x}{2}-4\)​

x²-ax+b = 0 மற்றும் x²-ex+f= 0  ஆகிய சமன்பாடுகளுக்கு ஒரு பொதுவான மூலம் உள்ளது. மேலும், இரண்டாம் சமன்பாட்டிற்குச் சமமான மூலங்கள் உண்டு எனில் ae=2(b+f) என நிறுவுக.

கீழ்க்காணும் விகிதமுறு கோவைகளைப் பகுதி பின்னங்களாகப் பிரித்தெழுதுக.
\(\frac{(x-1)^2}{x^3+x}\)

\(\frac { \cos ^{ 4 }{ \alpha } }{ \cos ^{ 2 }{ \beta } } +\frac { \sin ^{ 4 }{ \alpha } }{ \sin ^{ 4 }{ \beta } } =1\) எனில், \(\sin ^{ 4 }{ \alpha } +\sin ^{ 4 }{ \beta } =2\sin ^{ 2 }{ \alpha } \sin ^{ 2 }{ \beta } \) என நிறுவுக.

cosec\(\theta\) - sin \(\theta\) = a³ மற்றும் sec\(\theta\) - cos b\(\theta\)  = b³ எனில், a²b² (a² + b²) = 1 என நிறுவுக.

\(A+B+C={ 180 }^{ o }\) எனில், \(\cos { A } +\cos { B } -\cos { C } =-1+4\cos { \frac { A }{ 2 } } \cos { \frac { B }{ 2 } } \cos { \frac { C }{ 2 } } \) என நிறுவுக.

\(\triangle\)ABC இல் (a^2 ₊ b² +c²) tan B  = (a²+ b²-c²)tan C என நிறுவுக

கணிதத் தொகுத்தறிதல் மூலம், எல்லா முழு எண்கள்  n≥1-க்கு \(1^{2}+2^{2}+3^{2}+....+n^{2}=\frac{n(+1)(2n+1)}{6}\)என நிறுவுக.

தொகுத்தறிதலைப் பயன்படுத்தி எல்லா ஒரு இயல் எண் n-க்கும் 5ⁿ⁺¹+4ｘ6ⁿ ஐ 20 ஆல் வகுக்க கிடைக்கும் மீதி 9 என நிரூபிக்க.

கணிதத் தொகுத்தறிதலின்படி i² =-1 எனக் கொண்டு எந்த ஒரு இயல் எண் n-க்கும் \((r(cos\theta+isin\theta))^{n}=r^{n}(cosn \theta+isinn\theta)\) எனக் காட்டுக.

x ஒரு பெரிய எண் எனில் \(\sqrt [ 3 ]{ { x }^{ 3 }+7 } -\sqrt [ 3 ]{ { x }^{ 3}+4 } \) ன் மதிப்பு தோராயமாக \(\frac {1}{x^2}\) என நிறுவுக.

ஒரு வங்கியில் செலுத்தப்பட்ட ரூ 500 ஆனது, 10% தொடர் வட்டி வீதத்தில், 10 ஆண்டுகளில் எவ்வளவாக மாறும்.

θ ஒரு துணையலகு எனில் x = a cos³ θ,  y = a sin³ θ ஆகிய ஆயத்தொலைகளை உடைய நகரும் புள்ளியின் நியமப்பாதையின் சமன்பாட்டைக் காண்க.

ஆய அச்சுகளுக்கு இடையே ஒரு கோட்டுத் துண்டின் மையப் புள்ளி p(r, c) எனில் அந்த நேர்க்கோட்டின் சமன்பாடு \(\frac { x }{ r } +\frac { y }{ c } \)=2 எனக் காட்டுக.

ஒரு குடும்பம் 14.2 கிகி எடை கொண்ட சமையல் எரிவாயுவினை (LPG) (உருளையின் எடையுடன் 29.5 கிகி) சீரான முறையில் பயன்படுத்தும்போது 24 –வது நாளில் சமையல் எரிவாயுத் தீர்ந்து விடுகிறது. உடனடியாக புதிய எரிவாயு உருளை இணைக்கப்படுகிறது.
i) உருளையிலுள்ள சமையல் எரிவாயுவின் அளவிற்கும் மற்றும் பயன்படுத்தப்பட்ட நாட்களுக்கும் உள்ள தொடர்புடைய சமன்பாட்டைக் காண்க.
ii) சமையல் எரிவாயுவினை முதல் 96 நாட்கள் பயன்படுத்துவதற்கான வரைபடம் வரைக.

3x + 4y - 12 = 0 என்ற நேர்க்கோட்டிற்கு i) செங்குத்தான ii) இணையான நேர்க்கோடுகளின் தொகுப்பினைக் காண்க

y = x என்ற கோட்டுடன் a கோணத்தை உடைய, ஆதி வழிச் செல்லும் இரட்டைக் கோடுகளின் சமன்பாடு  \(x^2-2xy\ \sec 2\alpha +y^2=0\) என காண்பி.

\(A=\left[ \begin{matrix} 4 & 6 & 2 \\ 0 & 1 & 5 \\ 0 & 3 & 2 \end{matrix} \right] \) மற்றும் \(B=\left[ \begin{matrix} 0 & 1 & -1 \\ 3 & -1 & 4 \\ -1 & 2 & 1 \end{matrix} \right] \)  எனில், பின்வருவனவற்றைச் சரிபார்க்க.  \({ (AB) }^{ T }={ B }^{ T }{ A }^{ T }\)

\(\left| \begin{matrix} 1 & { x }^{ 2 } & { x }^{ 3 } \\ 1 & { y }^{ 2 } & { y }^{ 3 } \\ 1 & { z }^{ 2 } & { z }^{ 3 } \end{matrix} \right| =(x-y)(y-z)(z-x)(xy+yz+zx)\) என நிறுவுக. 

\(\left| \begin{matrix} 2bc-a^{ 2 } & { c }^{ 2 } & { b }^{ 2 } \\ { c }^{ 2 } & { 2ca-b }^{ 2 } & a^{ 2 } \\ { b }^{ 2 } & a^{ 2 } & { 2ab-c }^{ 2 } \end{matrix} \right| =\left| \begin{matrix} a & b & c \\ b & c & a \\ c & a & b \end{matrix} \right| ^{ 2 }\) என நிறுவுக. 

\(A\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix} \right] =\left[ \begin{matrix} -7 & -8 & -9 \\ 2 & 4 & 6 \end{matrix} \right] \)என்ற அணிச்சமன்பாட்டினை நிறைவு செய்யும் A  என்ற அணியைக் காண்க.

\(\vec { a } \) மற்றும் \(\vec { b } \) ஆகியவை இணைகரத்தின் ஒரு பக்கத்தையும் ஒரு மூலைவிட்டத்தையும் குறித்தால் அதன் பிற பக்கங்களையும் மற்றொரு  மூலைவிட்டத்தினையும் காண்க.

ABCD என்ற நாற்கரத்தில் AC,BD-ன் நடுப்புள்ளிகள் E மற்றும் F ஆக இருப்பின் \(\overrightarrow { AB } +\overrightarrow { AD } +\overrightarrow { CB } +\overrightarrow { CD } =4\overrightarrow { EF } \)  என நிறுவுக.  

\(\vec { a } =(2\hat { i } +3\hat { j } +6\hat { k } ),\vec { b } =(6\hat { i } +2\hat { j } -3\hat { k } ),\vec { b } =(3\hat { i } -6\hat { j } +2\hat { k } )\) ஆகியவை ஒன்றுக்கொன்று செங்குத்து என நிரூபிக்க.

எந்தவொரு வெக்டர்  \(\vec { a } \)-க்கும் \(\left| \vec { a } \times \hat { i } \right| ^{ 2 }+\left| \vec { a } \times \hat { j } \right| ^{ 2 }+\left| \vec { a } \times \hat { k } \right| ^{ 2 }=2\left| \vec { a } \right| ^{ 2 }\) என நிரூபிக்க.

பின்வரும் சார்புகளுக்கு இடப்புற,வலப்புற எல்லைகளின் மதிப்பக காண்க.
\(x=-2\) -ல் \(f(x)=\frac { { x }^{ 2 }-4 }{ ({ x }^{ 2 }+4x+4)(x+3) } \)

கொடுக்கப்பட்ட சார்புக்குக் கொடுக்கப்பட்ட புள்ளி x_0-இல் தொடர்ச்சியானதா அல்லது  தொடர்ச்சியற்றதா எனக் காரணத்துடன் கூறுக .
\({ x }_{ 0 }=1,f(x)=\begin{cases} \frac { { x }^{ 2 }-1 }{ x-1 } ,\quad x\neq 1 \\ 2\quad ,\quad x=1 \end{cases}\quad \)

\({ x }^{ 2 }+x+1\)-ஐப் பொறுத்து \(\tan ^{ -1 }{ (1+{ x }^{ 2 }) } \) -ஐ வகையிடுக.  

மதிப்பிடுக.
\(\int{\frac{3x+5}{x^{2}+4x+7}}dx\)